Relaxed Equivariance via Multitask Learning

Incorporating equivariance as an inductive bias into deep learning architectures to take advantage of the data symmetry has been successful in multiple applications, such as chemistry and dynamical systems. In particular, roto-translations are crucial for effectively modeling geometric graphs and molecules, where understanding the 3D structures enhances generalization. However, equivariant models often pose challenges due to their high computational complexity. In this paper, we introduce REMUL, a training procedure for approximating equivariance with multitask learning. We show that unconstrained models (which do not build equivariance into the architecture) can learn approximate symmetries by minimizing an additional simple equivariance loss. By formulating equivariance as a new learning objective, we can control the level of approximate equivariance in the model. Our method achieves competitive performance compared to equivariant baselines while being $10 \times$ faster at inference and $2.5 \times$ at training.

Generating Molecular Conformer Fields

In this paper we tackle the problem of generating conformers of a molecule in 3D space given its molecular graph. We parameterize these conformers as continuous functions that map elements from the molecular graph to points in 3D space. We then formulate the problem of learning to generate conformers as learning a distribution over these functions using a diffusion generative model, called Molecular Conformer Fields (MCF). Our approach is simple and scalable, and achieves state-of-the-art performance on challenging molecular conformer generation benchmarks while making no assumptions about the explicit structure of molecules (e.g. modeling torsional angles). MCF represents an advance in extending diffusion models to handle complex scientific problems in a conceptually simple, scalable and effective manner.

Manifold Diffusion Fields

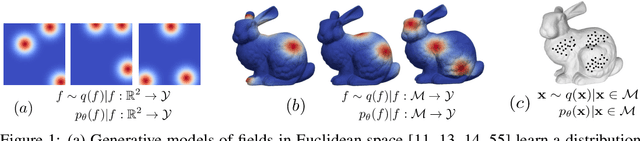
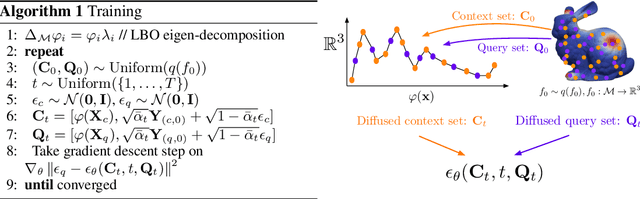
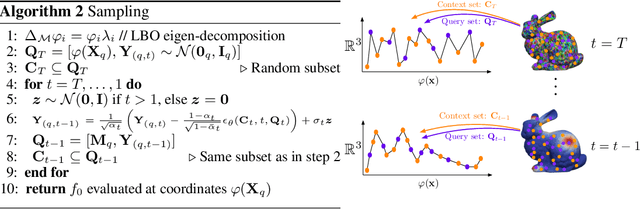
We present Manifold Diffusion Fields (MDF), an approach to learn generative models of continuous functions defined over Riemannian manifolds. Leveraging insights from spectral geometry analysis, we define an intrinsic coordinate system on the manifold via the eigen-functions of the Laplace-Beltrami Operator. MDF represents functions using an explicit parametrization formed by a set of multiple input-output pairs. Our approach allows to sample continuous functions on manifolds and is invariant with respect to rigid and isometric transformations of the manifold. Empirical results on several datasets and manifolds show that MDF can capture distributions of such functions with better diversity and fidelity than previous approaches.