Relaxed Equivariance via Multitask Learning

Incorporating equivariance as an inductive bias into deep learning architectures to take advantage of the data symmetry has been successful in multiple applications, such as chemistry and dynamical systems. In particular, roto-translations are crucial for effectively modeling geometric graphs and molecules, where understanding the 3D structures enhances generalization. However, equivariant models often pose challenges due to their high computational complexity. In this paper, we introduce REMUL, a training procedure for approximating equivariance with multitask learning. We show that unconstrained models (which do not build equivariance into the architecture) can learn approximate symmetries by minimizing an additional simple equivariance loss. By formulating equivariance as a new learning objective, we can control the level of approximate equivariance in the model. Our method achieves competitive performance compared to equivariant baselines while being $10 \times$ faster at inference and $2.5 \times$ at training.

Oscillatory State-Space Models

We propose Linear Oscillatory State-Space models (LinOSS) for efficiently learning on long sequences. Inspired by cortical dynamics of biological neural networks, we base our proposed LinOSS model on a system of forced harmonic oscillators. A stable discretization, integrated over time using fast associative parallel scans, yields the proposed state-space model. We prove that LinOSS produces stable dynamics only requiring nonnegative diagonal state matrix. This is in stark contrast to many previous state-space models relying heavily on restrictive parameterizations. Moreover, we rigorously show that LinOSS is universal, i.e., it can approximate any continuous and causal operator mapping between time-varying functions, to desired accuracy. In addition, we show that an implicit-explicit discretization of LinOSS perfectly conserves the symmetry of time reversibility of the underlying dynamics. Together, these properties enable efficient modeling of long-range interactions, while ensuring stable and accurate long-horizon forecasting. Finally, our empirical results, spanning a wide range of time-series tasks from mid-range to very long-range classification and regression, as well as long-horizon forecasting, demonstrate that our proposed LinOSS model consistently outperforms state-of-the-art sequence models. Notably, LinOSS outperforms Mamba by nearly 2x and LRU by 2.5x on a sequence modeling task with sequences of length 50k.

Improving Efficiency of Sampling-based Motion Planning via Message-Passing Monte Carlo

Sampling-based motion planning methods, while effective in high-dimensional spaces, often suffer from inefficiencies due to irregular sampling distributions, leading to suboptimal exploration of the configuration space. In this paper, we propose an approach that enhances the efficiency of these methods by utilizing low-discrepancy distributions generated through Message-Passing Monte Carlo (MPMC). MPMC leverages Graph Neural Networks (GNNs) to generate point sets that uniformly cover the space, with uniformity assessed using the the $\cL_p$-discrepancy measure, which quantifies the irregularity of sample distributions. By improving the uniformity of the point sets, our approach significantly reduces computational overhead and the number of samples required for solving motion planning problems. Experimental results demonstrate that our method outperforms traditional sampling techniques in terms of planning efficiency.

Message-Passing Monte Carlo: Generating low-discrepancy point sets via Graph Neural Networks

Discrepancy is a well-known measure for the irregularity of the distribution of a point set. Point sets with small discrepancy are called low-discrepancy and are known to efficiently fill the space in a uniform manner. Low-discrepancy points play a central role in many problems in science and engineering, including numerical integration, computer vision, machine perception, computer graphics, machine learning, and simulation. In this work, we present the first machine learning approach to generate a new class of low-discrepancy point sets named Message-Passing Monte Carlo (MPMC) points. Motivated by the geometric nature of generating low-discrepancy point sets, we leverage tools from Geometric Deep Learning and base our model on Graph Neural Networks. We further provide an extension of our framework to higher dimensions, which flexibly allows the generation of custom-made points that emphasize the uniformity in specific dimensions that are primarily important for the particular problem at hand. Finally, we demonstrate that our proposed model achieves state-of-the-art performance superior to previous methods by a significant margin. In fact, MPMC points are empirically shown to be either optimal or near-optimal with respect to the discrepancy for every dimension and the number of points for which the optimal discrepancy can be determined.

How does over-squashing affect the power of GNNs?

Graph Neural Networks (GNNs) are the state-of-the-art model for machine learning on graph-structured data. The most popular class of GNNs operate by exchanging information between adjacent nodes, and are known as Message Passing Neural Networks (MPNNs). Given their widespread use, understanding the expressive power of MPNNs is a key question. However, existing results typically consider settings with uninformative node features. In this paper, we provide a rigorous analysis to determine which function classes of node features can be learned by an MPNN of a given capacity. We do so by measuring the level of pairwise interactions between nodes that MPNNs allow for. This measure provides a novel quantitative characterization of the so-called over-squashing effect, which is observed to occur when a large volume of messages is aggregated into fixed-size vectors. Using our measure, we prove that, to guarantee sufficient communication between pairs of nodes, the capacity of the MPNN must be large enough, depending on properties of the input graph structure, such as commute times. For many relevant scenarios, our analysis results in impossibility statements in practice, showing that over-squashing hinders the expressive power of MPNNs. We validate our theoretical findings through extensive controlled experiments and ablation studies.

Neural Oscillators are Universal

Coupled oscillators are being increasingly used as the basis of machine learning (ML) architectures, for instance in sequence modeling, graph representation learning and in physical neural networks that are used in analog ML devices. We introduce an abstract class of neural oscillators that encompasses these architectures and prove that neural oscillators are universal, i.e, they can approximate any continuous and casual operator mapping between time-varying functions, to desired accuracy. This universality result provides theoretical justification for the use of oscillator based ML systems. The proof builds on a fundamental result of independent interest, which shows that a combination of forced harmonic oscillators with a nonlinear read-out suffices to approximate the underlying operators.

A Survey on Oversmoothing in Graph Neural Networks

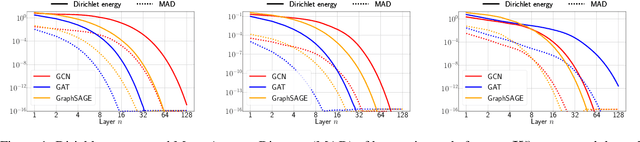
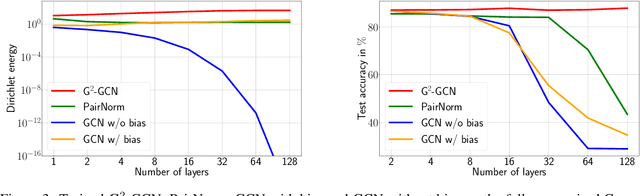
Node features of graph neural networks (GNNs) tend to become more similar with the increase of the network depth. This effect is known as over-smoothing, which we axiomatically define as the exponential convergence of suitable similarity measures on the node features. Our definition unifies previous approaches and gives rise to new quantitative measures of over-smoothing. Moreover, we empirically demonstrate this behavior for several over-smoothing measures on different graphs (small-, medium-, and large-scale). We also review several approaches for mitigating over-smoothing and empirically test their effectiveness on real-world graph datasets. Through illustrative examples, we demonstrate that mitigating over-smoothing is a necessary but not sufficient condition for building deep GNNs that are expressive on a wide range of graph learning tasks. Finally, we extend our definition of over-smoothing to the rapidly emerging field of continuous-time GNNs.

Multi-Scale Message Passing Neural PDE Solvers

We propose a novel multi-scale message passing neural network algorithm for learning the solutions of time-dependent PDEs. Our algorithm possesses both temporal and spatial multi-scale resolution features by incorporating multi-scale sequence models and graph gating modules in the encoder and processor, respectively. Benchmark numerical experiments are presented to demonstrate that the proposed algorithm outperforms baselines, particularly on a PDE with a range of spatial and temporal scales.

Gradient Gating for Deep Multi-Rate Learning on Graphs

We present Gradient Gating (G$^2$), a novel framework for improving the performance of Graph Neural Networks (GNNs). Our framework is based on gating the output of GNN layers with a mechanism for multi-rate flow of message passing information across nodes of the underlying graph. Local gradients are harnessed to further modulate message passing updates. Our framework flexibly allows one to use any basic GNN layer as a wrapper around which the multi-rate gradient gating mechanism is built. We rigorously prove that G$^2$ alleviates the oversmoothing problem and allows the design of deep GNNs. Empirical results are presented to demonstrate that the proposed framework achieves state-of-the-art performance on a variety of graph learning tasks, including on large-scale heterophilic graphs.

Graph-Coupled Oscillator Networks

We propose Graph-Coupled Oscillator Networks (GraphCON), a novel framework for deep learning on graphs. It is based on discretizations of a second-order system of ordinary differential equations (ODEs), which model a network of nonlinear forced and damped oscillators, coupled via the adjacency structure of the underlying graph. The flexibility of our framework permits any basic GNN layer (e.g. convolutional or attentional) as the coupling function, from which a multi-layer deep neural network is built up via the dynamics of the proposed ODEs. We relate the oversmoothing problem, commonly encountered in GNNs, to the stability of steady states of the underlying ODE and show that zero-Dirichlet energy steady states are not stable for our proposed ODEs. This demonstrates that the proposed framework mitigates the oversmoothing problem. Finally, we show that our approach offers competitive performance with respect to the state-of-the-art on a variety of graph-based learning tasks.