What makes a good feedforward computational graph?

As implied by the plethora of literature on graph rewiring, the choice of computational graph employed by a neural network can make a significant impact on its downstream performance. Certain effects related to the computational graph, such as under-reaching and over-squashing, may even render the model incapable of learning certain functions. Most of these effects have only been thoroughly studied in the domain of undirected graphs; however, recent years have seen a significant rise in interest in feedforward computational graphs: directed graphs without any back edges. In this paper, we study the desirable properties of a feedforward computational graph, discovering two important complementary measures: fidelity and mixing time, and evaluating a few popular choices of graphs through the lens of these measures. Our study is backed by both theoretical analyses of the metrics' asymptotic behaviour for various graphs, as well as correlating these metrics to the performance of trained neural network models using the corresponding graphs.

The unknotting number, hard unknot diagrams, and reinforcement learning

We have developed a reinforcement learning agent that often finds a minimal sequence of unknotting crossing changes for a knot diagram with up to 200 crossings, hence giving an upper bound on the unknotting number. We have used this to determine the unknotting number of 57k knots. We took diagrams of connected sums of such knots with oppositely signed signatures, where the summands were overlaid. The agent has found examples where several of the crossing changes in an unknotting collection of crossings result in hyperbolic knots. Based on this, we have shown that, given knots $K$ and $K'$ that satisfy some mild assumptions, there is a diagram of their connected sum and $u(K) + u(K')$ unknotting crossings such that changing any one of them results in a prime knot. As a by-product, we have obtained a dataset of 2.6 million distinct hard unknot diagrams; most of them under 35 crossings. Assuming the additivity of the unknotting number, we have determined the unknotting number of 43 at most 12-crossing knots for which the unknotting number is unknown.

How does over-squashing affect the power of GNNs?

Graph Neural Networks (GNNs) are the state-of-the-art model for machine learning on graph-structured data. The most popular class of GNNs operate by exchanging information between adjacent nodes, and are known as Message Passing Neural Networks (MPNNs). Given their widespread use, understanding the expressive power of MPNNs is a key question. However, existing results typically consider settings with uninformative node features. In this paper, we provide a rigorous analysis to determine which function classes of node features can be learned by an MPNN of a given capacity. We do so by measuring the level of pairwise interactions between nodes that MPNNs allow for. This measure provides a novel quantitative characterization of the so-called over-squashing effect, which is observed to occur when a large volume of messages is aggregated into fixed-size vectors. Using our measure, we prove that, to guarantee sufficient communication between pairs of nodes, the capacity of the MPNN must be large enough, depending on properties of the input graph structure, such as commute times. For many relevant scenarios, our analysis results in impossibility statements in practice, showing that over-squashing hinders the expressive power of MPNNs. We validate our theoretical findings through extensive controlled experiments and ablation studies.

Expander Graph Propagation

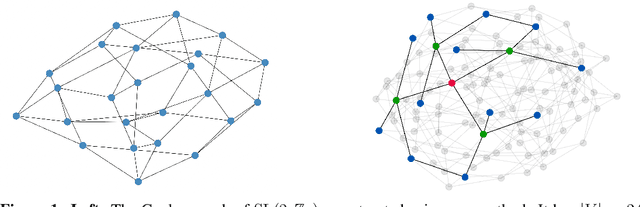
Deploying graph neural networks (GNNs) on whole-graph classification or regression tasks is known to be challenging: it often requires computing node features that are mindful of both local interactions in their neighbourhood and the global context of the graph structure. GNN architectures that navigate this space need to avoid pathological behaviours, such as bottlenecks and oversquashing, while ideally having linear time and space complexity requirements. In this work, we propose an elegant approach based on propagating information over expander graphs. We provide an efficient method for constructing expander graphs of a given size, and use this insight to propose the EGP model. We show that EGP is able to address all of the above concerns, while requiring minimal effort to set up, and provide evidence of its empirical utility on relevant datasets and baselines in the Open Graph Benchmark. Importantly, using expander graphs as a template for message passing necessarily gives rise to negative curvature. While this appears to be counterintuitive in light of recent related work on oversquashing, we theoretically demonstrate that negatively curved edges are likely to be required to obtain scalable message passing without bottlenecks. To the best of our knowledge, this is a previously unstudied result in the context of graph representation learning, and we believe our analysis paves the way to a novel class of scalable methods to counter oversquashing in GNNs.

The signature and cusp geometry of hyperbolic knots

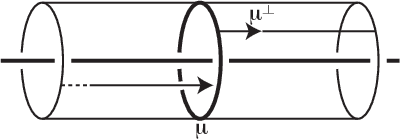
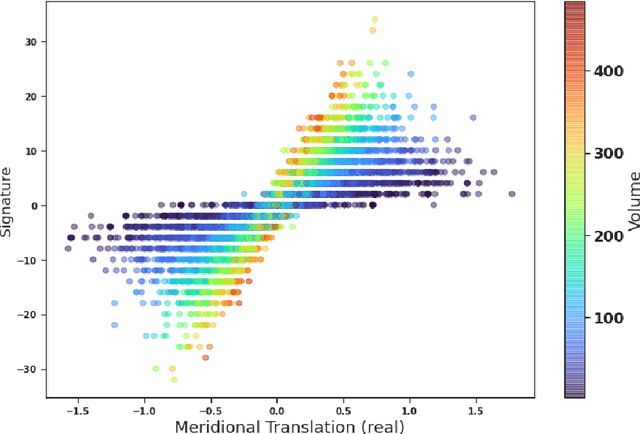
We introduce a new real-valued invariant called the natural slope of a hyperbolic knot in the 3-sphere, which is defined in terms of its cusp geometry. We show that twice the knot signature and the natural slope differ by at most a constant times the hyperbolic volume divided by the cube of the injectivity radius. This inequality was discovered using machine learning to detect relationships between various knot invariants. It has applications to Dehn surgery and to 4-ball genus. We also show a refined version of the inequality where the upper bound is a linear function of the volume, and the slope is corrected by terms corresponding to short geodesics that link the knot an odd number of times.