AlphaEvolve: A coding agent for scientific and algorithmic discovery

In this white paper, we present AlphaEvolve, an evolutionary coding agent that substantially enhances capabilities of state-of-the-art LLMs on highly challenging tasks such as tackling open scientific problems or optimizing critical pieces of computational infrastructure. AlphaEvolve orchestrates an autonomous pipeline of LLMs, whose task is to improve an algorithm by making direct changes to the code. Using an evolutionary approach, continuously receiving feedback from one or more evaluators, AlphaEvolve iteratively improves the algorithm, potentially leading to new scientific and practical discoveries. We demonstrate the broad applicability of this approach by applying it to a number of important computational problems. When applied to optimizing critical components of large-scale computational stacks at Google, AlphaEvolve developed a more efficient scheduling algorithm for data centers, found a functionally equivalent simplification in the circuit design of hardware accelerators, and accelerated the training of the LLM underpinning AlphaEvolve itself. Furthermore, AlphaEvolve discovered novel, provably correct algorithms that surpass state-of-the-art solutions on a spectrum of problems in mathematics and computer science, significantly expanding the scope of prior automated discovery methods (Romera-Paredes et al., 2023). Notably, AlphaEvolve developed a search algorithm that found a procedure to multiply two $4 \times 4$ complex-valued matrices using $48$ scalar multiplications; offering the first improvement, after 56 years, over Strassen's algorithm in this setting. We believe AlphaEvolve and coding agents like it can have a significant impact in improving solutions of problems across many areas of science and computation.

The unknotting number, hard unknot diagrams, and reinforcement learning

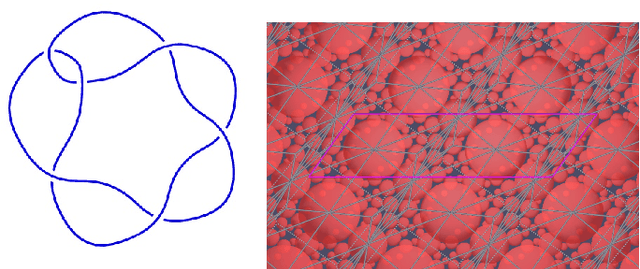
We have developed a reinforcement learning agent that often finds a minimal sequence of unknotting crossing changes for a knot diagram with up to 200 crossings, hence giving an upper bound on the unknotting number. We have used this to determine the unknotting number of 57k knots. We took diagrams of connected sums of such knots with oppositely signed signatures, where the summands were overlaid. The agent has found examples where several of the crossing changes in an unknotting collection of crossings result in hyperbolic knots. Based on this, we have shown that, given knots $K$ and $K'$ that satisfy some mild assumptions, there is a diagram of their connected sum and $u(K) + u(K')$ unknotting crossings such that changing any one of them results in a prime knot. As a by-product, we have obtained a dataset of 2.6 million distinct hard unknot diagrams; most of them under 35 crossings. Assuming the additivity of the unknotting number, we have determined the unknotting number of 43 at most 12-crossing knots for which the unknotting number is unknown.

Learning to Decode the Surface Code with a Recurrent, Transformer-Based Neural Network

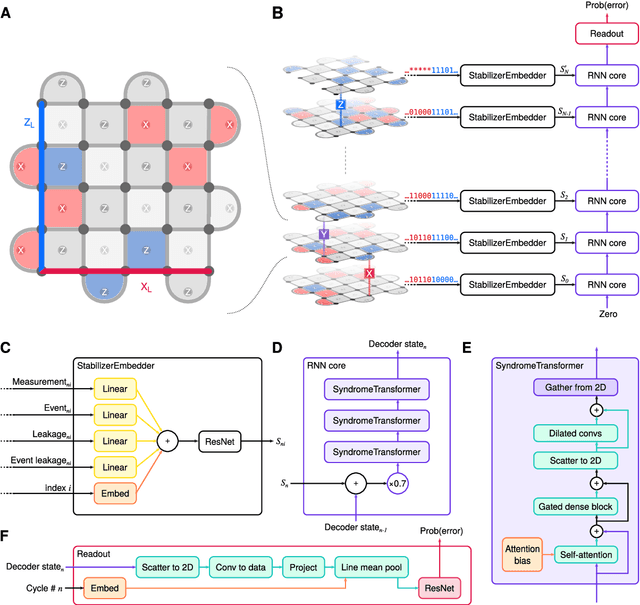
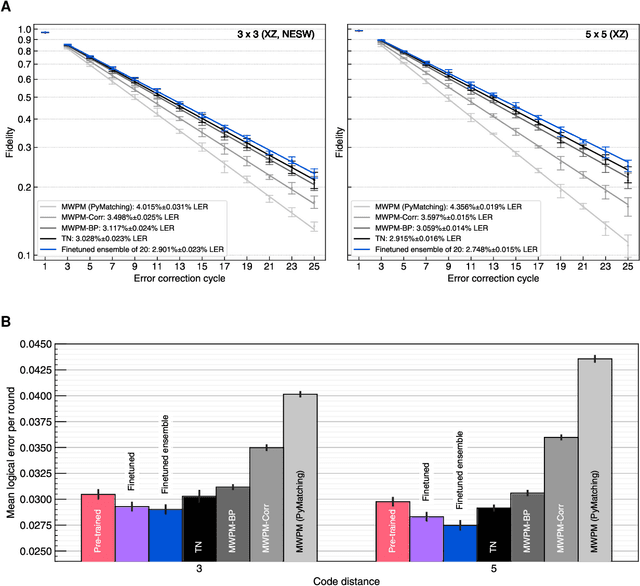
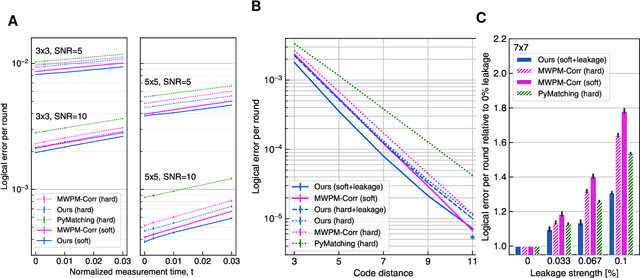
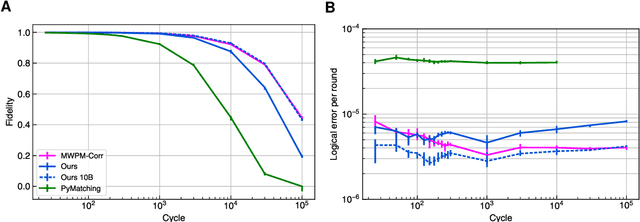
Quantum error-correction is a prerequisite for reliable quantum computation. Towards this goal, we present a recurrent, transformer-based neural network which learns to decode the surface code, the leading quantum error-correction code. Our decoder outperforms state-of-the-art algorithmic decoders on real-world data from Google's Sycamore quantum processor for distance 3 and 5 surface codes. On distances up to 11, the decoder maintains its advantage on simulated data with realistic noise including cross-talk, leakage, and analog readout signals, and sustains its accuracy far beyond the 25 cycles it was trained on. Our work illustrates the ability of machine learning to go beyond human-designed algorithms by learning from data directly, highlighting machine learning as a strong contender for decoding in quantum computers.

Realistic Synthetic Social Networks with Graph Neural Networks

Social network analysis faces profound difficulties in sharing data between researchers due to privacy and security concerns. A potential remedy to this issue are synthetic networks, that closely resemble their real counterparts, but can be freely distributed. generating synthetic networks requires the creation of network topologies that, in application, function as realistically as possible. Widely applied models are currently rule-based and can struggle to reproduce structural dynamics. Lead by recent developments in Graph Neural Network (GNN) models for network generation we evaluate the potential of GNNs for synthetic social networks. Our GNN use is specifically within a reasonable use-case and includes empirical evaluation using Maximum Mean Discrepancy (MMD). We include social network specific measurements which allow evaluation of how realistically synthetic networks behave in typical social network analysis applications. We find that the Gated Recurrent Attention Network (GRAN) extends well to social networks, and in comparison to a benchmark popular rule-based generation Recursive-MATrix (R-MAT) method, is better able to replicate realistic structural dynamics. We find that GRAN is more computationally costly than R-MAT, but is not excessively costly to employ, so would be effective for researchers seeking to create datasets of synthetic social networks.

The signature and cusp geometry of hyperbolic knots

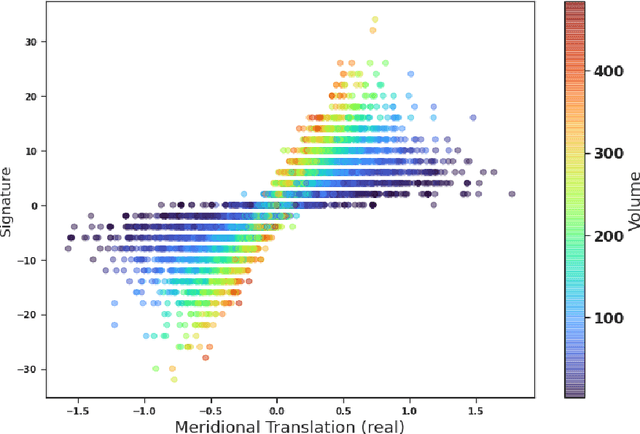
We introduce a new real-valued invariant called the natural slope of a hyperbolic knot in the 3-sphere, which is defined in terms of its cusp geometry. We show that twice the knot signature and the natural slope differ by at most a constant times the hyperbolic volume divided by the cube of the injectivity radius. This inequality was discovered using machine learning to detect relationships between various knot invariants. It has applications to Dehn surgery and to 4-ball genus. We also show a refined version of the inequality where the upper bound is a linear function of the volume, and the slope is corrected by terms corresponding to short geodesics that link the knot an odd number of times.

The Random Forest Kernel and other kernels for big data from random partitions

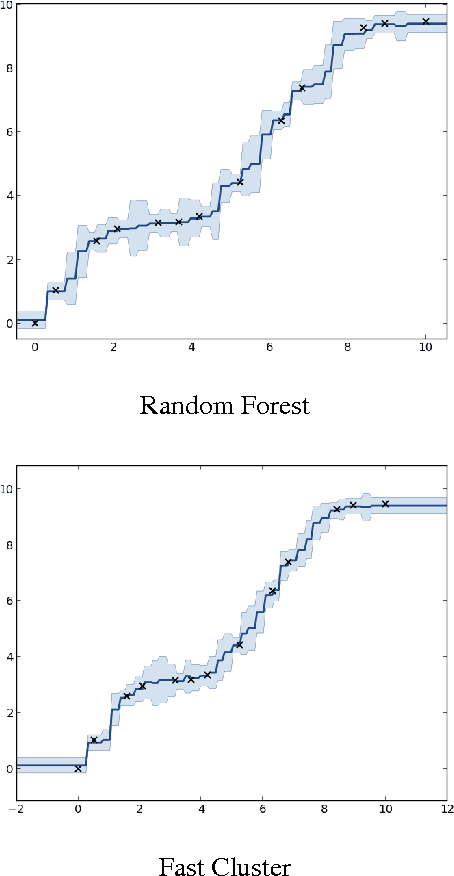
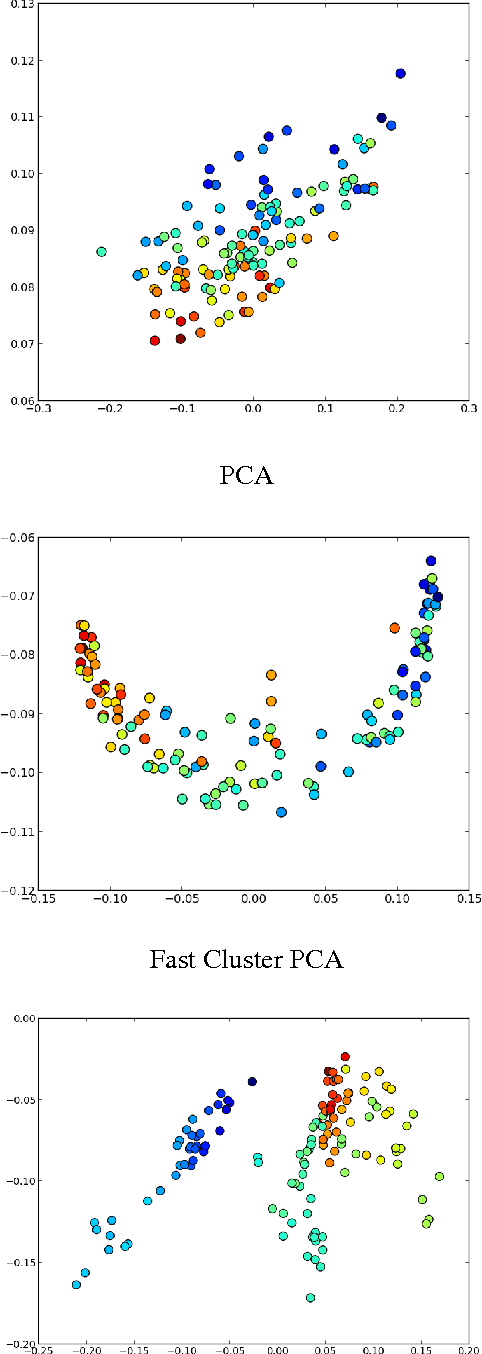
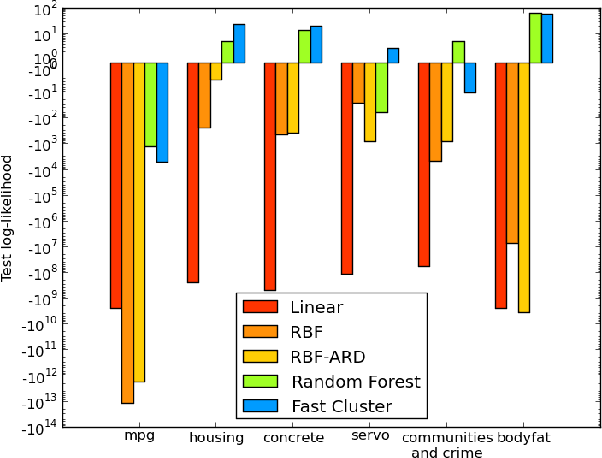
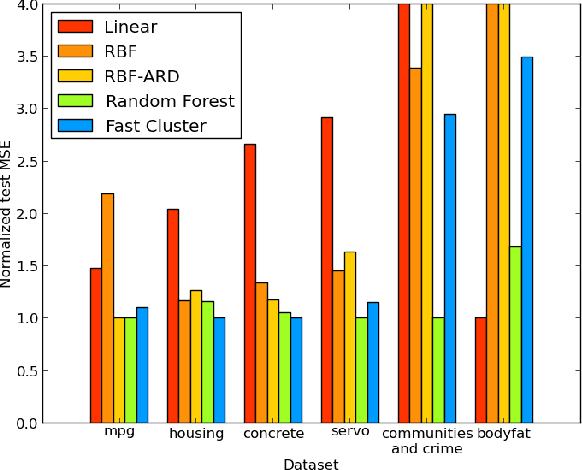
We present Random Partition Kernels, a new class of kernels derived by demonstrating a natural connection between random partitions of objects and kernels between those objects. We show how the construction can be used to create kernels from methods that would not normally be viewed as random partitions, such as Random Forest. To demonstrate the potential of this method, we propose two new kernels, the Random Forest Kernel and the Fast Cluster Kernel, and show that these kernels consistently outperform standard kernels on problems involving real-world datasets. Finally, we show how the form of these kernels lend themselves to a natural approximation that is appropriate for certain big data problems, allowing $O(N)$ inference in methods such as Gaussian Processes, Support Vector Machines and Kernel PCA.

SiGMa: Simple Greedy Matching for Aligning Large Knowledge Bases

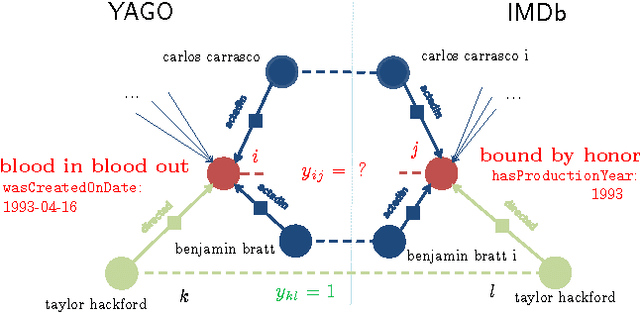
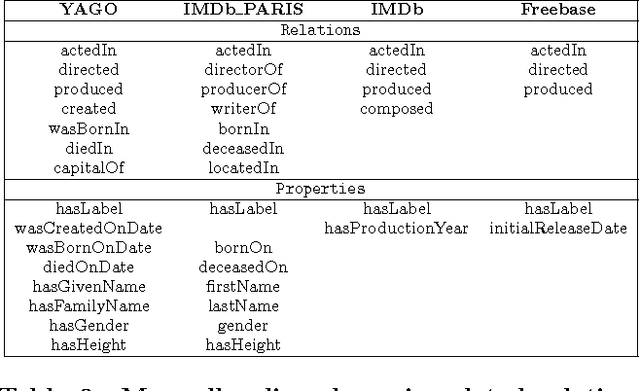
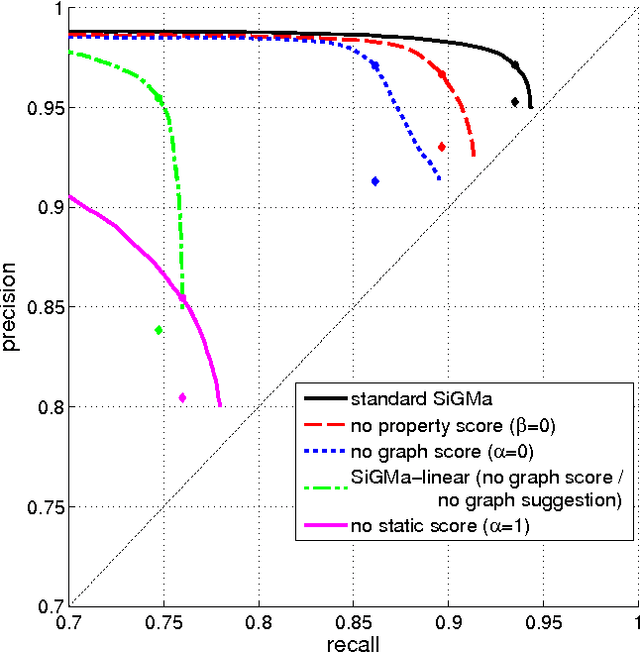
The Internet has enabled the creation of a growing number of large-scale knowledge bases in a variety of domains containing complementary information. Tools for automatically aligning these knowledge bases would make it possible to unify many sources of structured knowledge and answer complex queries. However, the efficient alignment of large-scale knowledge bases still poses a considerable challenge. Here, we present Simple Greedy Matching (SiGMa), a simple algorithm for aligning knowledge bases with millions of entities and facts. SiGMa is an iterative propagation algorithm which leverages both the structural information from the relationship graph as well as flexible similarity measures between entity properties in a greedy local search, thus making it scalable. Despite its greedy nature, our experiments indicate that SiGMa can efficiently match some of the world's largest knowledge bases with high precision. We provide additional experiments on benchmark datasets which demonstrate that SiGMa can outperform state-of-the-art approaches both in accuracy and efficiency.