AlphaEvolve: A coding agent for scientific and algorithmic discovery

In this white paper, we present AlphaEvolve, an evolutionary coding agent that substantially enhances capabilities of state-of-the-art LLMs on highly challenging tasks such as tackling open scientific problems or optimizing critical pieces of computational infrastructure. AlphaEvolve orchestrates an autonomous pipeline of LLMs, whose task is to improve an algorithm by making direct changes to the code. Using an evolutionary approach, continuously receiving feedback from one or more evaluators, AlphaEvolve iteratively improves the algorithm, potentially leading to new scientific and practical discoveries. We demonstrate the broad applicability of this approach by applying it to a number of important computational problems. When applied to optimizing critical components of large-scale computational stacks at Google, AlphaEvolve developed a more efficient scheduling algorithm for data centers, found a functionally equivalent simplification in the circuit design of hardware accelerators, and accelerated the training of the LLM underpinning AlphaEvolve itself. Furthermore, AlphaEvolve discovered novel, provably correct algorithms that surpass state-of-the-art solutions on a spectrum of problems in mathematics and computer science, significantly expanding the scope of prior automated discovery methods (Romera-Paredes et al., 2023). Notably, AlphaEvolve developed a search algorithm that found a procedure to multiply two $4 \times 4$ complex-valued matrices using $48$ scalar multiplications; offering the first improvement, after 56 years, over Strassen's algorithm in this setting. We believe AlphaEvolve and coding agents like it can have a significant impact in improving solutions of problems across many areas of science and computation.

A Note on Small Percolating Sets on Hypercubes via Generative AI

We apply a generative AI pattern-recognition technique called PatternBoost to study bootstrap percolation on hypercubes. With this, we slightly improve the best existing upper bound for the size of percolating subsets of the hypercube.

PatternBoost: Constructions in Mathematics with a Little Help from AI

We introduce PatternBoost, a flexible method for finding interesting constructions in mathematics. Our algorithm alternates between two phases. In the first ``local'' phase, a classical search algorithm is used to produce many desirable constructions. In the second ``global'' phase, a transformer neural network is trained on the best such constructions. Samples from the trained transformer are then used as seeds for the first phase, and the process is repeated. We give a detailed introduction to this technique, and discuss the results of its application to several problems in extremal combinatorics. The performance of PatternBoost varies across different problems, but there are many situations where its performance is quite impressive. Using our technique, we find the best known solutions to several long-standing problems, including the construction of a counterexample to a conjecture that had remained open for 30 years.

Finding Increasingly Large Extremal Graphs with AlphaZero and Tabu Search

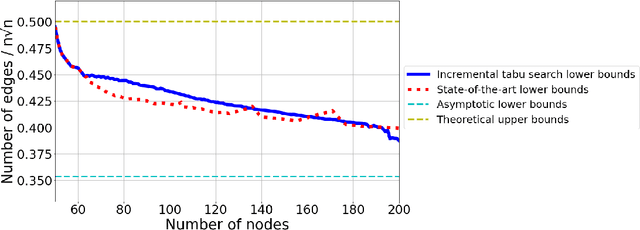
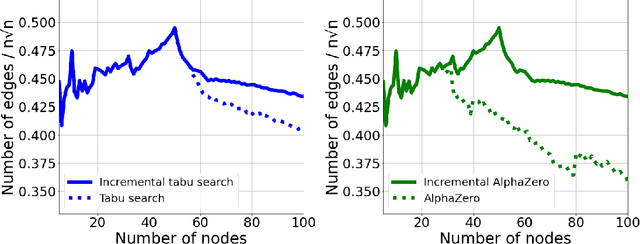
This work studies a central extremal graph theory problem inspired by a 1975 conjecture of Erd\H{o}s, which aims to find graphs with a given size (number of nodes) that maximize the number of edges without having 3- or 4-cycles. We formulate this problem as a sequential decision-making problem and compare AlphaZero, a neural network-guided tree search, with tabu search, a heuristic local search method. Using either method, by introducing a curriculum -- jump-starting the search for larger graphs using good graphs found at smaller sizes -- we improve the state-of-the-art lower bounds for several sizes. We also propose a flexible graph-generation environment and a permutation-invariant network architecture for learning to search in the space of graphs.

Constructions in combinatorics via neural networks

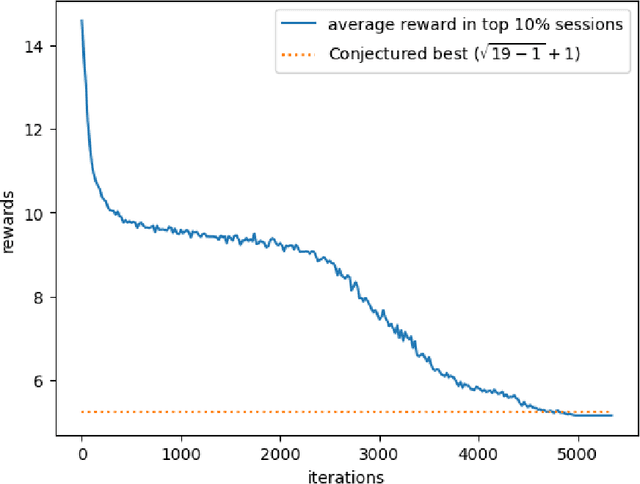
We demonstrate how by using a reinforcement learning algorithm, the deep cross-entropy method, one can find explicit constructions and counterexamples to several open conjectures in extremal combinatorics and graph theory. Amongst the conjectures we refute are a question of Brualdi and Cao about maximizing permanents of pattern avoiding matrices, and several problems related to the adjacency and distance eigenvalues of graphs.