Finding Increasingly Large Extremal Graphs with AlphaZero and Tabu Search

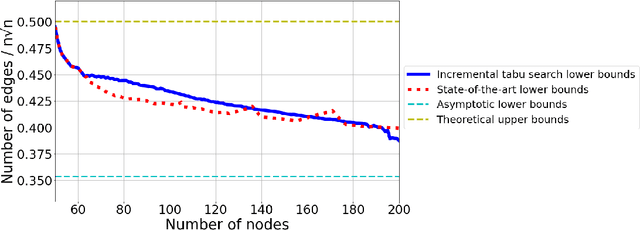
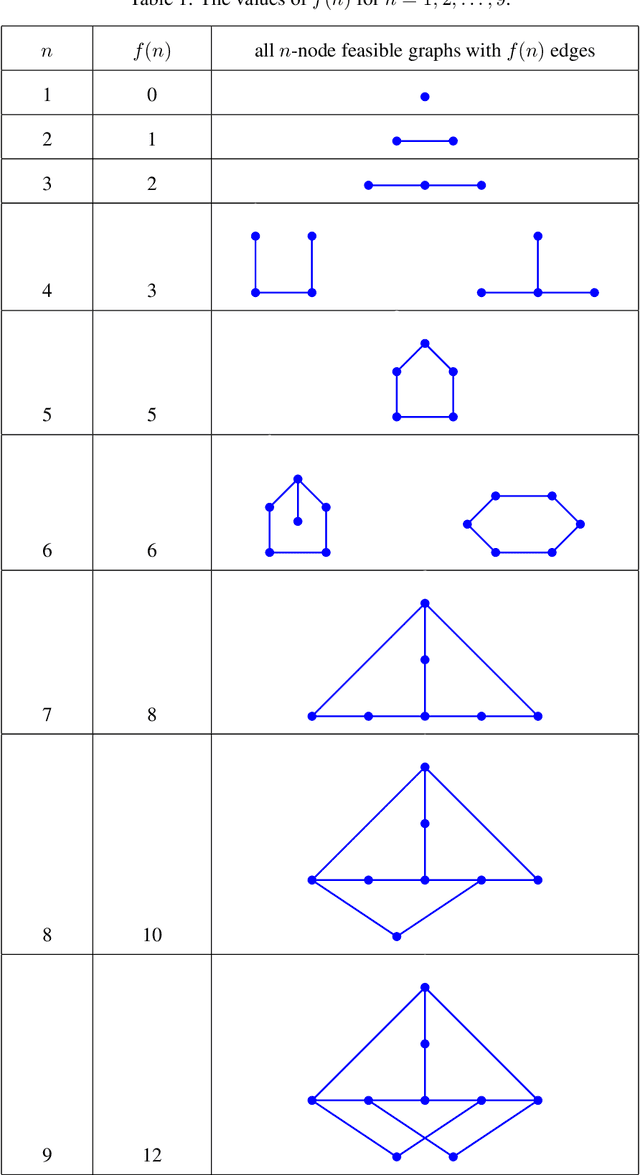
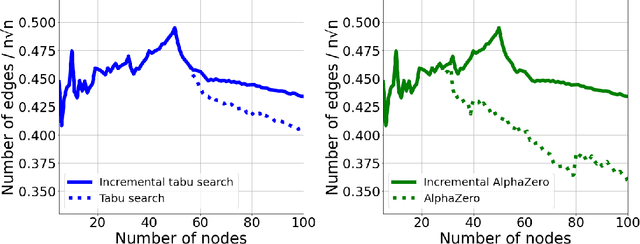
This work studies a central extremal graph theory problem inspired by a 1975 conjecture of Erd\H{o}s, which aims to find graphs with a given size (number of nodes) that maximize the number of edges without having 3- or 4-cycles. We formulate this problem as a sequential decision-making problem and compare AlphaZero, a neural network-guided tree search, with tabu search, a heuristic local search method. Using either method, by introducing a curriculum -- jump-starting the search for larger graphs using good graphs found at smaller sizes -- we improve the state-of-the-art lower bounds for several sizes. We also propose a flexible graph-generation environment and a permutation-invariant network architecture for learning to search in the space of graphs.

Batched Multi-Armed Bandits with Optimal Regret

We present a simple and efficient algorithm for the batched stochastic multi-armed bandit problem. We prove a bound for its expected regret that improves over the best-known regret bound, for any number of batches. In particular, our algorithm achieves the optimal expected regret by using only a logarithmic number of batches.

Old Dog Learns New Tricks: Randomized UCB for Bandit Problems

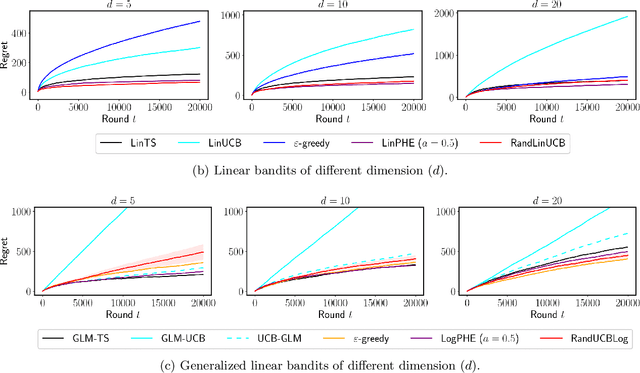
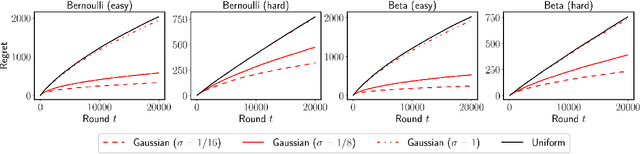
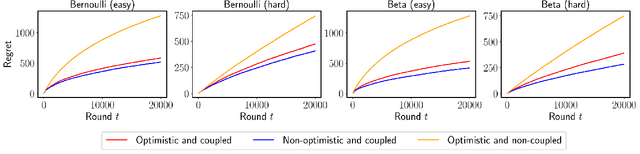
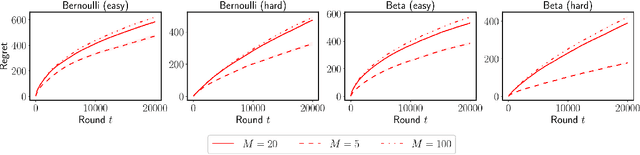
We propose $\tt RandUCB$, a bandit strategy that uses theoretically derived confidence intervals similar to upper confidence bound (UCB) algorithms, but akin to Thompson sampling (TS), uses randomization to trade off exploration and exploitation. In the $K$-armed bandit setting, we show that there are infinitely many variants of $\tt RandUCB$, all of which achieve the minimax-optimal $\widetilde{O}(\sqrt{K T})$ regret after $T$ rounds. Moreover, in a specific multi-armed bandit setting, we show that both UCB and TS can be recovered as special cases of $\tt RandUCB.$ For structured bandits, where each arm is associated with a $d$-dimensional feature vector and rewards are distributed according to a linear or generalized linear model, we prove that $\tt RandUCB$ achieves the minimax-optimal $\widetilde{O}(d \sqrt{T})$ regret even in the case of infinite arms. We demonstrate the practical effectiveness of $\tt RandUCB$ with experiments in both the multi-armed and structured bandit settings. Our results illustrate that $\tt RandUCB$ matches the empirical performance of TS while obtaining the theoretically optimal regret bounds of UCB algorithms, thus achieving the best of both worlds.

New Algorithms for Multiplayer Bandits when Arm Means Vary Among Players

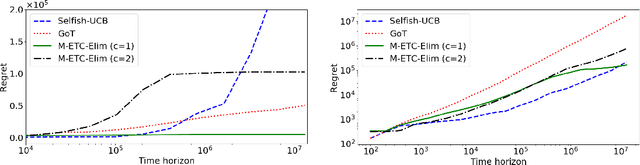
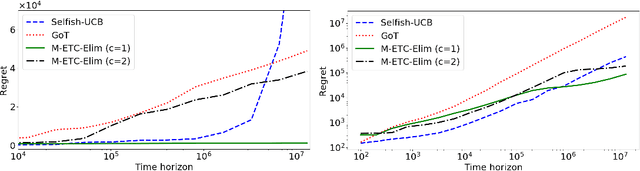
We study multiplayer stochastic multi-armed bandit problems in which the players cannot communicate,and if two or more players pull the same arm, a collision occurs and the involved players receive zero reward.Moreover, we assume each arm has a different mean for each player. Let $T$ denote the number of rounds.An algorithm with regret $O((\log T)^{2+\kappa})$ for any constant $\kappa$ was recently presented by Bistritz and Leshem (NeurIPS 2018), who left the existence of an algorithm with $O(\log T)$ regret as an open question. In this paper, we provide an affirmative answer to this question in the case when there is a unique optimal assignment of players to arms. For the general case we present an algorithm with expected regret $O((\log T)^{1+\kappa})$, for any $\kappa>0$.

Multiplayer bandits without observing collision information

We study multiplayer stochastic multi-armed bandit problems in which the players cannot communicate, and if two or more players pull the same arm, a collision occurs and the involved players receive zero reward. We consider two feedback models: a model in which the players can observe whether a collision has occurred, and a more difficult setup when no collision information is available. We give the first theoretical guarantees for the second model: an algorithm with a logarithmic regret, and an algorithm with a square-root regret type that does not depend on the gaps between the means. For the first model, we give the first square-root regret bounds that do not depend on the gaps. Building on these ideas, we also give an algorithm for reaching approximate Nash equilibria quickly in stochastic anti-coordination games.

The Minimax Learning Rate of Normal and Ising Undirected Graphical Models

Let $G$ be an undirected graph with $m$ edges and $d$ vertices. We show that $d$-dimensional Ising models on $G$ can be learned from $n$ i.i.d. samples within expected total variation distance some constant factor of $\min\{1, \sqrt{(m + d)/n}\}$, and that this rate is optimal. We show that the same rate holds for the class of $d$-dimensional multivariate normal undirected graphical models with respect to $G$. We also identify the optimal rate of $\min\{1, \sqrt{m/n}\}$ for Ising models with no external magnetic field.

Sample-Efficient Learning of Mixtures

We consider PAC learning of probability distributions (a.k.a. density estimation), where we are given an i.i.d. sample generated from an unknown target distribution, and want to output a distribution that is close to the target in total variation distance. Let $\mathcal F$ be an arbitrary class of probability distributions, and let $\mathcal{F}^k$ denote the class of $k$-mixtures of elements of $\mathcal F$. Assuming the existence of a method for learning $\mathcal F$ with sample complexity $m_{\mathcal{F}}(\epsilon)$, we provide a method for learning $\mathcal F^k$ with sample complexity $O({k\log k \cdot m_{\mathcal F}(\epsilon) }/{\epsilon^{2}})$. Our mixture learning algorithm has the property that, if the $\mathcal F$-learner is proper/agnostic, then the $\mathcal F^k$-learner would be proper/agnostic as well. This general result enables us to improve the best known sample complexity upper bounds for a variety of important mixture classes. First, we show that the class of mixtures of $k$ axis-aligned Gaussians in $\mathbb{R}^d$ is PAC-learnable in the agnostic setting with $\widetilde{O}({kd}/{\epsilon ^ 4})$ samples, which is tight in $k$ and $d$ up to logarithmic factors. Second, we show that the class of mixtures of $k$ Gaussians in $\mathbb{R}^d$ is PAC-learnable in the agnostic setting with sample complexity $\widetilde{O}({kd^2}/{\epsilon ^ 4})$, which improves the previous known bounds of $\widetilde{O}({k^3d^2}/{\epsilon ^ 4})$ and $\widetilde{O}(k^4d^4/\epsilon ^ 2)$ in its dependence on $k$ and $d$. Finally, we show that the class of mixtures of $k$ log-concave distributions over $\mathbb{R}^d$ is PAC-learnable using $\widetilde{O}(d^{(d+5)/2}\epsilon^{-(d+9)/2}k)$ samples.

Some techniques in density estimation

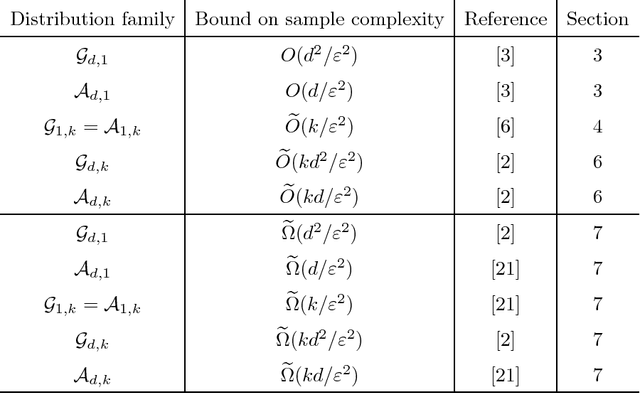
Density estimation is an interdisciplinary topic at the intersection of statistics, theoretical computer science and machine learning. We review some old and new techniques for bounding the sample complexity of estimating densities of continuous distributions, focusing on the class of mixtures of Gaussians and its subclasses. In particular, we review the main techniques used to prove the new sample complexity bounds for mixtures of Gaussians by Ashtiani, Ben-David, Harvey, Liaw, Mehrabian, and Plan arXiv:1710.05209.

Settling the Sample Complexity for Learning Mixtures of Gaussians

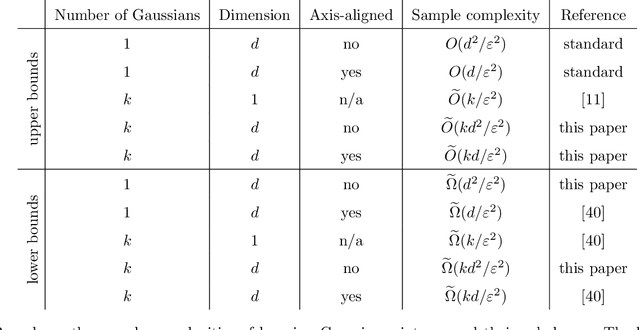
We prove that $\widetilde{\Theta}(k d^2 / \varepsilon^2)$ samples are necessary and sufficient for learning a mixture of $k$ Gaussians in $\mathbf{R}^d$, up to error $\varepsilon$ in total variation distance. This improves both the known upper bound and lower bound for this problem. For mixtures of axis-aligned Gaussians, we show that $\widetilde{O}(k d / \varepsilon^2)$ samples suffice, matching a known lower bound. Moreover, these results hold in an agnostic learning setting as well. The upper bound is based on a novel technique for distribution learning based on a notion of sample compression. Any class of distributions that allows such a sample compression scheme can also be learned with few samples. Moreover, if a class of distributions has such a compression scheme, then so do the classes of products and mixtures of those distributions. The core of our main result is showing that the class of Gaussians in $\mathbf{R}^d$ has an efficient sample compression.

Nearly-tight VC-dimension and pseudodimension bounds for piecewise linear neural networks

We prove new upper and lower bounds on the VC-dimension of deep neural networks with the ReLU activation function. These bounds are tight for almost the entire range of parameters. Letting $W$ be the number of weights and $L$ be the number of layers, we prove that the VC-dimension is $O(W L \log(W))$, and provide examples with VC-dimension $\Omega( W L \log(W/L) )$. This improves both the previously known upper bounds and lower bounds. In terms of the number $U$ of non-linear units, we prove a tight bound $\Theta(W U)$ on the VC-dimension. All of these bounds generalize to arbitrary piecewise linear activation functions, and also hold for the pseudodimensions of these function classes. Combined with previous results, this gives an intriguing range of dependencies of the VC-dimension on depth for networks with different non-linearities: there is no dependence for piecewise-constant, linear dependence for piecewise-linear, and no more than quadratic dependence for general piecewise-polynomial.