Old Dog Learns New Tricks: Randomized UCB for Bandit Problems
Paper and Code
Oct 11, 2019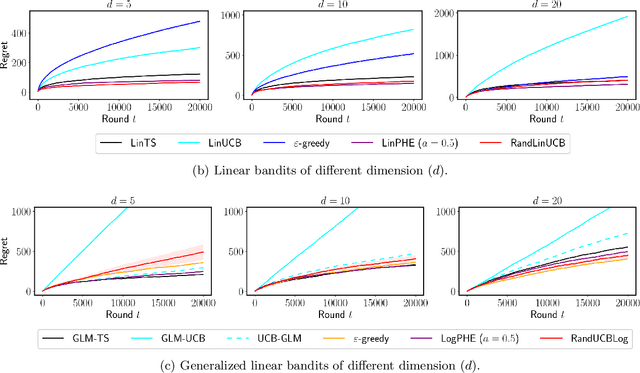
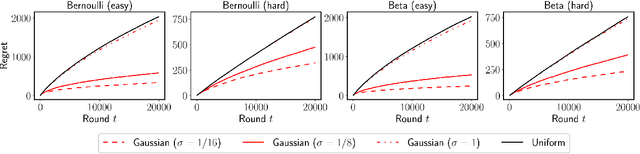
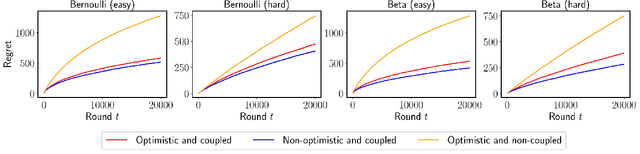
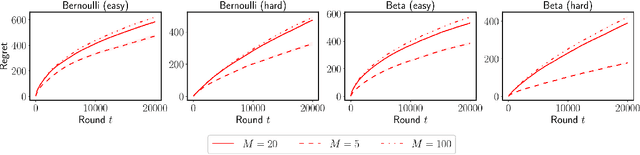
We propose $\tt RandUCB$, a bandit strategy that uses theoretically derived confidence intervals similar to upper confidence bound (UCB) algorithms, but akin to Thompson sampling (TS), uses randomization to trade off exploration and exploitation. In the $K$-armed bandit setting, we show that there are infinitely many variants of $\tt RandUCB$, all of which achieve the minimax-optimal $\widetilde{O}(\sqrt{K T})$ regret after $T$ rounds. Moreover, in a specific multi-armed bandit setting, we show that both UCB and TS can be recovered as special cases of $\tt RandUCB.$ For structured bandits, where each arm is associated with a $d$-dimensional feature vector and rewards are distributed according to a linear or generalized linear model, we prove that $\tt RandUCB$ achieves the minimax-optimal $\widetilde{O}(d \sqrt{T})$ regret even in the case of infinite arms. We demonstrate the practical effectiveness of $\tt RandUCB$ with experiments in both the multi-armed and structured bandit settings. Our results illustrate that $\tt RandUCB$ matches the empirical performance of TS while obtaining the theoretically optimal regret bounds of UCB algorithms, thus achieving the best of both worlds.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge