Sample Complexity Bounds for Linear Constrained MDPs with a Generative Model

We consider infinite-horizon $\gamma$-discounted (linear) constrained Markov decision processes (CMDPs) where the objective is to find a policy that maximizes the expected cumulative reward subject to expected cumulative constraints. Given access to a generative model, we propose to solve CMDPs with a primal-dual framework that can leverage any black-box unconstrained MDP solver. For linear CMDPs with feature dimension $d$, we instantiate the framework by using mirror descent value iteration (\texttt{MDVI})~\citep{kitamura2023regularization} an example MDP solver. We provide sample complexity bounds for the resulting CMDP algorithm in two cases: (i) relaxed feasibility, where small constraint violations are allowed, and (ii) strict feasibility, where the output policy is required to exactly satisfy the constraint. For (i), we prove that the algorithm can return an $\epsilon$-optimal policy with high probability by using $\tilde{O}\left(\frac{d^2}{(1-\gamma)^4\epsilon^2}\right)$ samples. We note that these results exhibit a near-optimal dependence on both $d$ and $\epsilon$. For (ii), we show that the algorithm requires $\tilde{O}\left(\frac{d^2}{(1-\gamma)^6\epsilon^2\zeta^2}\right)$ samples, where $\zeta$ is the problem-dependent Slater constant that characterizes the size of the feasible region. Finally, we instantiate our framework for tabular CMDPs and show that it can be used to recover near-optimal sample complexities in this setting.

Glocal Smoothness: Line Search can really help!

Iteration complexities for first-order optimization algorithms are typically stated in terms of a global Lipschitz constant of the gradient, and near-optimal results are achieved using fixed step sizes. But many objective functions that arise in practice have regions with small Lipschitz constants where larger step sizes can be used. Many local Lipschitz assumptions have been proposed, which have lead to results showing that adaptive step sizes and/or line searches yield improved convergence rates over fixed step sizes. However, these faster rates tend to depend on the iterates of the algorithm, which makes it difficult to compare the iteration complexities of different methods. We consider a simple characterization of global and local ("glocal") smoothness that only depends on properties of the function. This allows upper bounds on iteration complexities in terms of iterate-independent constants and enables us to compare iteration complexities between algorithms. Under this assumption it is straightforward to show the advantages of line searches over fixed step sizes, and that in some settings, gradient descent with line search has a better iteration complexity than accelerated methods with fixed step sizes. We further show that glocal smoothness can lead to improved complexities for the Polyak and AdGD step sizes, as well other algorithms including coordinate optimization, stochastic gradient methods, accelerated gradient methods, and non-linear conjugate gradient methods.

Preserving Plasticity in Continual Learning with Adaptive Linearity Injection

Loss of plasticity in deep neural networks is the gradual reduction in a model's capacity to incrementally learn and has been identified as a key obstacle to learning in non-stationary problem settings. Recent work has shown that deep linear networks tend to be resilient towards loss of plasticity. Motivated by this observation, we propose Adaptive Linearization (AdaLin), a general approach that dynamically adapts each neuron's activation function to mitigate plasticity loss. Unlike prior methods that rely on regularization or periodic resets, AdaLin equips every neuron with a learnable parameter and a gating mechanism that injects linearity into the activation function based on its gradient flow. This adaptive modulation ensures sufficient gradient signal and sustains continual learning without introducing additional hyperparameters or requiring explicit task boundaries. When used with conventional activation functions like ReLU, Tanh, and GeLU, we demonstrate that AdaLin can significantly improve performance on standard benchmarks, including Random Label and Permuted MNIST, Random Label and Shuffled CIFAR-10, and Class-Split CIFAR-100. Furthermore, its efficacy is shown in more complex scenarios, such as class-incremental learning on CIFAR-100 with a ResNet-18 backbone, and in mitigating plasticity loss in off-policy reinforcement learning agents. We perform a systematic set of ablations that show that neuron-level adaptation is crucial for good performance and analyze a number of metrics in the network that might be correlated to loss of plasticity.

Rethinking the Global Convergence of Softmax Policy Gradient with Linear Function Approximation

Policy gradient (PG) methods have played an essential role in the empirical successes of reinforcement learning. In order to handle large state-action spaces, PG methods are typically used with function approximation. In this setting, the approximation error in modeling problem-dependent quantities is a key notion for characterizing the global convergence of PG methods. We focus on Softmax PG with linear function approximation (referred to as $\texttt{Lin-SPG}$) and demonstrate that the approximation error is irrelevant to the algorithm's global convergence even for the stochastic bandit setting. Consequently, we first identify the necessary and sufficient conditions on the feature representation that can guarantee the asymptotic global convergence of $\texttt{Lin-SPG}$. Under these feature conditions, we prove that $T$ iterations of $\texttt{Lin-SPG}$ with a problem-specific learning rate result in an $O(1/T)$ convergence to the optimal policy. Furthermore, we prove that $\texttt{Lin-SPG}$ with any arbitrary constant learning rate can ensure asymptotic global convergence to the optimal policy.

Small steps no more: Global convergence of stochastic gradient bandits for arbitrary learning rates

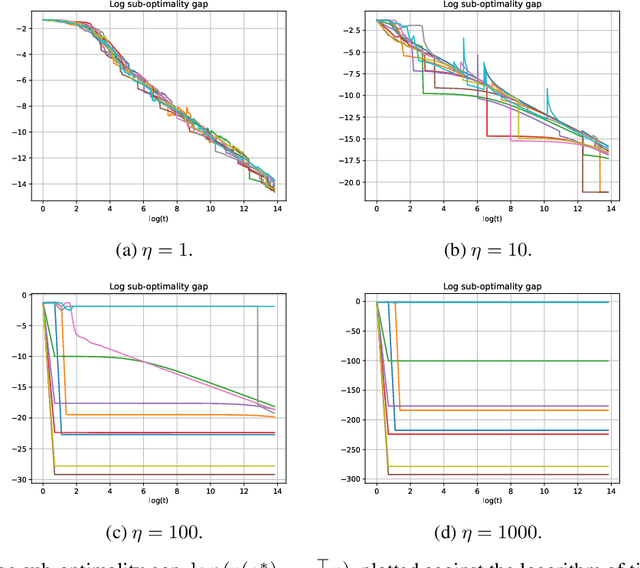
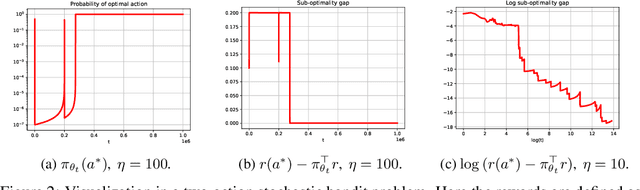
We provide a new understanding of the stochastic gradient bandit algorithm by showing that it converges to a globally optimal policy almost surely using \emph{any} constant learning rate. This result demonstrates that the stochastic gradient algorithm continues to balance exploration and exploitation appropriately even in scenarios where standard smoothness and noise control assumptions break down. The proofs are based on novel findings about action sampling rates and the relationship between cumulative progress and noise, and extend the current understanding of how simple stochastic gradient methods behave in bandit settings.

Improving OOD Generalization of Pre-trained Encoders via Aligned Embedding-Space Ensembles

The quality of self-supervised pre-trained embeddings on out-of-distribution (OOD) data is poor without fine-tuning. A straightforward and simple approach to improving the generalization of pre-trained representation to OOD data is the use of deep ensembles. However, obtaining an effective ensemble in the embedding space with only unlabeled data remains an unsolved problem. We first perform a theoretical analysis that reveals the relationship between individual hyperspherical embedding spaces in an ensemble. We then design a principled method to align these embedding spaces in an unsupervised manner. Experimental results on the MNIST dataset show that our embedding-space ensemble method improves pre-trained embedding quality on in-distribution and OOD data compared to single encoders.

Fast Convergence of Softmax Policy Mirror Ascent

Natural policy gradient (NPG) is a common policy optimization algorithm and can be viewed as mirror ascent in the space of probabilities. Recently, Vaswani et al. [2021] introduced a policy gradient method that corresponds to mirror ascent in the dual space of logits. We refine this algorithm, removing its need for a normalization across actions and analyze the resulting method (referred to as SPMA). For tabular MDPs, we prove that SPMA with a constant step-size matches the linear convergence of NPG and achieves a faster convergence than constant step-size (accelerated) softmax policy gradient. To handle large state-action spaces, we extend SPMA to use a log-linear policy parameterization. Unlike that for NPG, generalizing SPMA to the linear function approximation (FA) setting does not require compatible function approximation. Unlike MDPO, a practical generalization of NPG, SPMA with linear FA only requires solving convex softmax classification problems. We prove that SPMA achieves linear convergence to the neighbourhood of the optimal value function. We extend SPMA to handle non-linear FA and evaluate its empirical performance on the MuJoCo and Atari benchmarks. Our results demonstrate that SPMA consistently achieves similar or better performance compared to MDPO, PPO and TRPO.

Towards Principled, Practical Policy Gradient for Bandits and Tabular MDPs

We consider (stochastic) softmax policy gradient (PG) methods for bandits and tabular Markov decision processes (MDPs). While the PG objective is non-concave, recent research has used the objective's smoothness and gradient domination properties to achieve convergence to an optimal policy. However, these theoretical results require setting the algorithm parameters according to unknown problem-dependent quantities (e.g. the optimal action or the true reward vector in a bandit problem). To address this issue, we borrow ideas from the optimization literature to design practical, principled PG methods in both the exact and stochastic settings. In the exact setting, we employ an Armijo line-search to set the step-size for softmax PG and empirically demonstrate a linear convergence rate. In the stochastic setting, we utilize exponentially decreasing step-sizes, and characterize the convergence rate of the resulting algorithm. We show that the proposed algorithm offers similar theoretical guarantees as the state-of-the art results, but does not require the knowledge of oracle-like quantities. For the multi-armed bandit setting, our techniques result in a theoretically-principled PG algorithm that does not require explicit exploration, the knowledge of the reward gap, the reward distributions, or the noise. Finally, we empirically compare the proposed methods to PG approaches that require oracle knowledge, and demonstrate competitive performance.

From Inverse Optimization to Feasibility to ERM

Inverse optimization involves inferring unknown parameters of an optimization problem from known solutions, and is widely used in fields such as transportation, power systems and healthcare. We study the contextual inverse optimization setting that utilizes additional contextual information to better predict the unknown problem parameters. We focus on contextual inverse linear programming (CILP), addressing the challenges posed by the non-differentiable nature of LPs. For a linear prediction model, we reduce CILP to a convex feasibility problem allowing the use of standard algorithms such as alternating projections. The resulting algorithm for CILP is equipped with a linear convergence guarantee without additional assumptions such as degeneracy or interpolation. Next, we reduce CILP to empirical risk minimization (ERM) on a smooth, convex loss that satisfies the Polyak-Lojasiewicz condition. This reduction enables the use of scalable first-order optimization methods to solve large non-convex problems, while maintaining theoretical guarantees in the convex setting. Finally, we experimentally validate our approach on both synthetic and real-world problems, and demonstrate improved performance compared to existing methods.

Noise-adaptive (Accelerated) Stochastic Heavy-Ball Momentum

We analyze the convergence of stochastic heavy ball (SHB) momentum in the smooth, strongly-convex setting. Kidambi et al. (2018) show that SHB (with small mini-batches) cannot attain an accelerated rate of convergence even for quadratics, and conjecture that the practical gain of SHB is a by-product of mini-batching. We substantiate this claim by showing that SHB can obtain an accelerated rate when the mini-batch size is larger than some threshold. In particular, for strongly-convex quadratics with condition number $\kappa$, we prove that SHB with the standard step-size and momentum parameters results in an $O\left(\exp(-\frac{T}{\sqrt{\kappa}}) + \sigma \right)$ convergence rate, where $T$ is the number of iterations and $\sigma^2$ is the variance in the stochastic gradients. To ensure convergence to the minimizer, we propose a multi-stage approach that results in a noise-adaptive $O\left(\exp\left(-\frac{T}{\sqrt{\kappa}} \right) + \frac{\sigma}{T}\right)$ rate. For general strongly-convex functions, we use the averaging interpretation of SHB along with exponential step-sizes to prove an $O\left(\exp\left(-\frac{T}{\kappa} \right) + \frac{\sigma^2}{T} \right)$ convergence to the minimizer in a noise-adaptive manner. Finally, we empirically demonstrate the effectiveness of the proposed algorithms.