Mark Schmidt
SIERRA, LIENS
Glocal Smoothness: Line Search can really help!
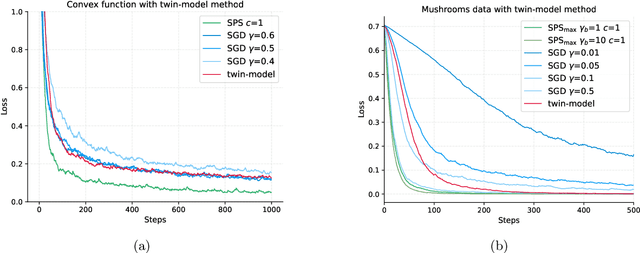
Jun 14, 2025Abstract:Iteration complexities for first-order optimization algorithms are typically stated in terms of a global Lipschitz constant of the gradient, and near-optimal results are achieved using fixed step sizes. But many objective functions that arise in practice have regions with small Lipschitz constants where larger step sizes can be used. Many local Lipschitz assumptions have been proposed, which have lead to results showing that adaptive step sizes and/or line searches yield improved convergence rates over fixed step sizes. However, these faster rates tend to depend on the iterates of the algorithm, which makes it difficult to compare the iteration complexities of different methods. We consider a simple characterization of global and local ("glocal") smoothness that only depends on properties of the function. This allows upper bounds on iteration complexities in terms of iterate-independent constants and enables us to compare iteration complexities between algorithms. Under this assumption it is straightforward to show the advantages of line searches over fixed step sizes, and that in some settings, gradient descent with line search has a better iteration complexity than accelerated methods with fixed step sizes. We further show that glocal smoothness can lead to improved complexities for the Polyak and AdGD step sizes, as well other algorithms including coordinate optimization, stochastic gradient methods, accelerated gradient methods, and non-linear conjugate gradient methods.
ReMA: Learning to Meta-think for LLMs with Multi-Agent Reinforcement Learning
Mar 12, 2025Abstract:Recent research on Reasoning of Large Language Models (LLMs) has sought to further enhance their performance by integrating meta-thinking -- enabling models to monitor, evaluate, and control their reasoning processes for more adaptive and effective problem-solving. However, current single-agent work lacks a specialized design for acquiring meta-thinking, resulting in low efficacy. To address this challenge, we introduce Reinforced Meta-thinking Agents (ReMA), a novel framework that leverages Multi-Agent Reinforcement Learning (MARL) to elicit meta-thinking behaviors, encouraging LLMs to think about thinking. ReMA decouples the reasoning process into two hierarchical agents: a high-level meta-thinking agent responsible for generating strategic oversight and plans, and a low-level reasoning agent for detailed executions. Through iterative reinforcement learning with aligned objectives, these agents explore and learn collaboration, leading to improved generalization and robustness. Experimental results demonstrate that ReMA outperforms single-agent RL baselines on complex reasoning tasks, including competitive-level mathematical benchmarks and LLM-as-a-Judge benchmarks. Comprehensive ablation studies further illustrate the evolving dynamics of each distinct agent, providing valuable insights into how the meta-thinking reasoning process enhances the reasoning capabilities of LLMs.
Implicit Bias of SignGD and Adam on Multiclass Separable Data
Feb 07, 2025
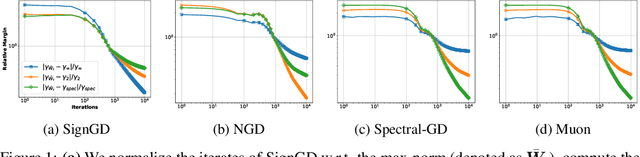
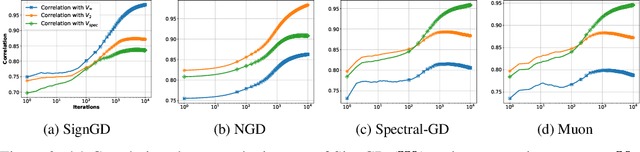
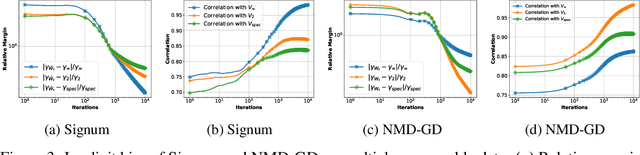
Abstract:In the optimization of overparameterized models, different gradient-based methods can achieve zero training error yet converge to distinctly different solutions inducing different generalization properties. While a decade of research on implicit optimization bias has illuminated this phenomenon in various settings, even the foundational case of linear classification with separable data still has important open questions. We resolve a fundamental gap by characterizing the implicit bias of both Adam and Sign Gradient Descent in multi-class cross-entropy minimization: we prove that their iterates converge to solutions that maximize the margin with respect to the classifier matrix's max-norm and characterize the rate of convergence. We extend our results to general p-norm normalized steepest descent algorithms and to other multi-class losses.
Don't Be So Positive: Negative Step Sizes in Second-Order Methods
Nov 18, 2024



Abstract:The value of second-order methods lies in the use of curvature information. Yet, this information is costly to extract and once obtained, valuable negative curvature information is often discarded so that the method is globally convergent. This limits the effectiveness of second-order methods in modern machine learning. In this paper, we show that second-order and second-order-like methods are promising optimizers for neural networks provided that we add one ingredient: negative step sizes. We show that under very general conditions, methods that produce ascent directions are globally convergent when combined with a Wolfe line search that allows both positive and negative step sizes. We experimentally demonstrate that using negative step sizes is often more effective than common Hessian modification methods.
BlockLLM: Memory-Efficient Adaptation of LLMs by Selecting and Optimizing the Right Coordinate Blocks
Jun 25, 2024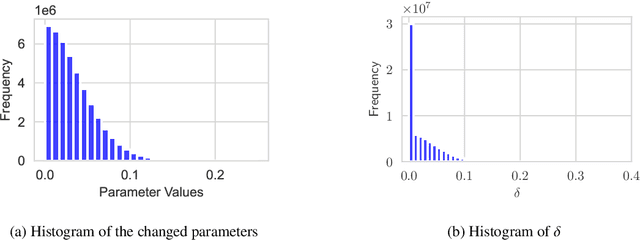
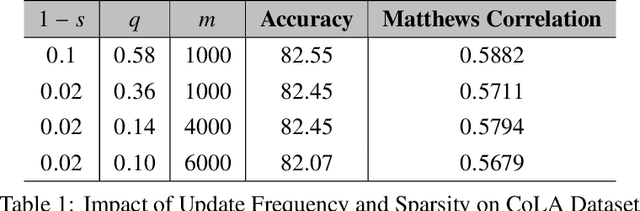

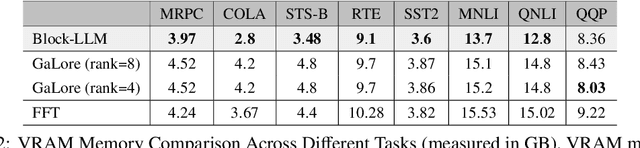
Abstract:Training large language models (LLMs) for pretraining or adapting to new tasks and domains has become increasingly critical as their applications expand. However, as the model and the data sizes grow, the training process presents significant memory challenges, often requiring a prohibitive amount of GPU memory that may not be readily available. Existing methods such as low-rank adaptation (LoRA) add trainable low-rank matrix factorizations, altering the training dynamics and limiting the model's parameter search to a low-rank subspace. GaLore, a more recent method, employs Gradient Low-Rank Projection to reduce the memory footprint, in the full parameter training setting. However GaLore can only be applied to a subset of the LLM layers that satisfy the "reversibility" property, thus limiting their applicability. In response to these challenges, we introduce BlockLLM, an approach inspired by block coordinate descent. Our method carefully selects and updates a very small subset of the trainable parameters without altering any part of its architecture and training procedure. BlockLLM achieves state-of-the-art performance in both finetuning and pretraining tasks, while reducing the memory footprint of the underlying optimization process. Our experiments demonstrate that fine-tuning with only less than 5% of the parameters, BlockLLM achieves state-of-the-art perplexity scores on the GLUE benchmarks. On Llama model pretrained on C4 dataset, BlockLLM is able to train with significantly less memory than the state-of-the-art, while still maintaining competitive performance.
Why Line Search when you can Plane Search? SO-Friendly Neural Networks allow Per-Iteration Optimization of Learning and Momentum Rates for Every Layer
Jun 25, 2024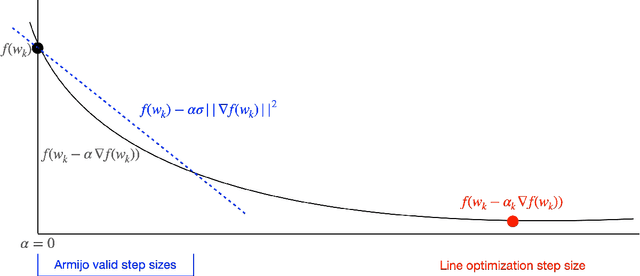
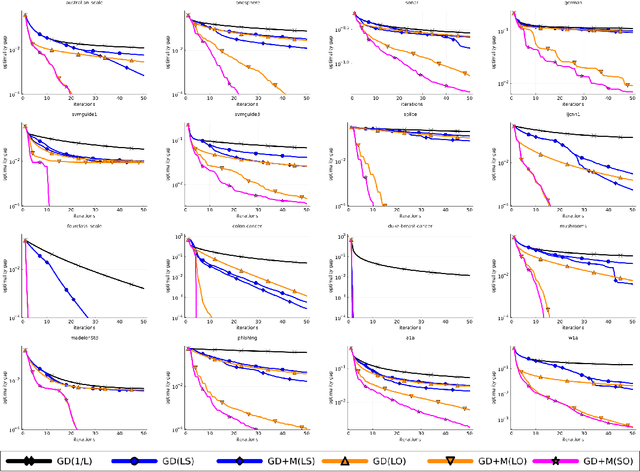
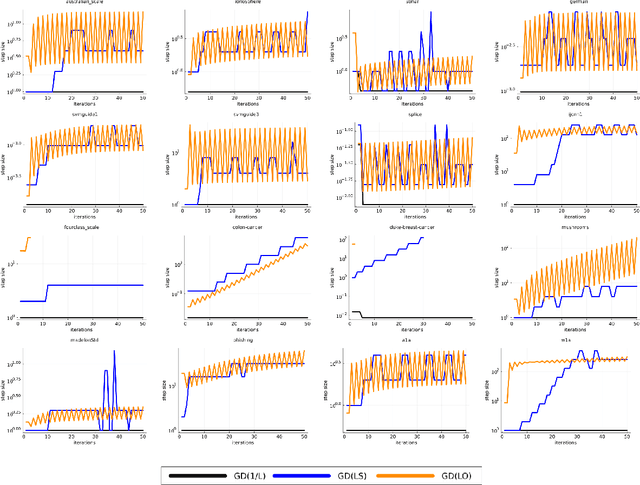
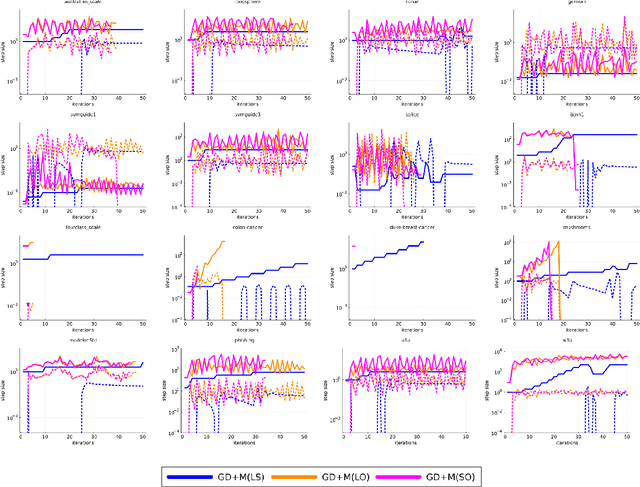
Abstract:We introduce the class of SO-friendly neural networks, which include several models used in practice including networks with 2 layers of hidden weights where the number of inputs is larger than the number of outputs. SO-friendly networks have the property that performing a precise line search to set the step size on each iteration has the same asymptotic cost during full-batch training as using a fixed learning. Further, for the same cost a planesearch can be used to set both the learning and momentum rate on each step. Even further, SO-friendly networks also allow us to use subspace optimization to set a learning rate and momentum rate for each layer on each iteration. We explore augmenting gradient descent as well as quasi-Newton methods and Adam with line optimization and subspace optimization, and our experiments indicate that this gives fast and reliable ways to train these networks that are insensitive to hyper-parameters.
Enhancing Policy Gradient with the Polyak Step-Size Adaption
Apr 11, 2024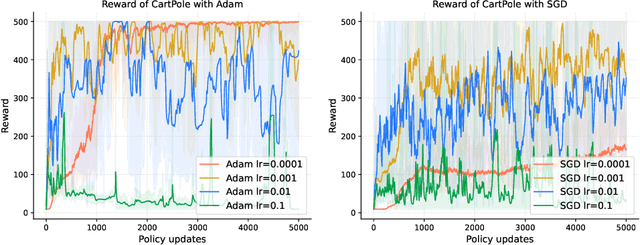
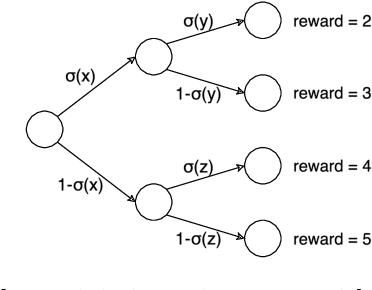
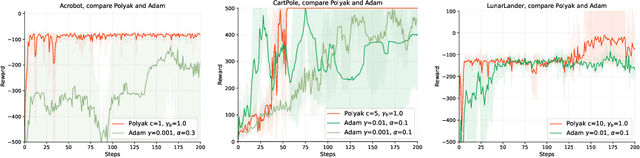
Abstract:Policy gradient is a widely utilized and foundational algorithm in the field of reinforcement learning (RL). Renowned for its convergence guarantees and stability compared to other RL algorithms, its practical application is often hindered by sensitivity to hyper-parameters, particularly the step-size. In this paper, we introduce the integration of the Polyak step-size in RL, which automatically adjusts the step-size without prior knowledge. To adapt this method to RL settings, we address several issues, including unknown f* in the Polyak step-size. Additionally, we showcase the performance of the Polyak step-size in RL through experiments, demonstrating faster convergence and the attainment of more stable policies.
Faster Convergence of Stochastic Accelerated Gradient Descent under Interpolation
Apr 03, 2024
Abstract:We prove new convergence rates for a generalized version of stochastic Nesterov acceleration under interpolation conditions. Unlike previous analyses, our approach accelerates any stochastic gradient method which makes sufficient progress in expectation. The proof, which proceeds using the estimating sequences framework, applies to both convex and strongly convex functions and is easily specialized to accelerated SGD under the strong growth condition. In this special case, our analysis reduces the dependence on the strong growth constant from $\rho$ to $\sqrt{\rho}$ as compared to prior work. This improvement is comparable to a square-root of the condition number in the worst case and address criticism that guarantees for stochastic acceleration could be worse than those for SGD.
Heavy-Tailed Class Imbalance and Why Adam Outperforms Gradient Descent on Language Models
Feb 29, 2024



Abstract:Adam has been shown to outperform gradient descent in optimizing large language transformers empirically, and by a larger margin than on other tasks, but it is unclear why this happens. We show that the heavy-tailed class imbalance found in language modeling tasks leads to difficulties in the optimization dynamics. When training with gradient descent, the loss associated with infrequent words decreases slower than the loss associated with frequent ones. As most samples come from relatively infrequent words, the average loss decreases slowly with gradient descent. On the other hand, Adam and sign-based methods do not suffer from this problem and improve predictions on all classes. To establish that this behavior is indeed caused by class imbalance, we show empirically that it persist through different architectures and data types, on language transformers, vision CNNs, and linear models. We further study this phenomenon on a linear classification with cross-entropy loss, showing that heavy-tailed class imbalance leads to ill-conditioning, and that the normalization used by Adam can counteract it.
Analyzing and Improving Greedy 2-Coordinate Updates for Equality-Constrained Optimization via Steepest Descent in the 1-Norm
Jul 03, 2023



Abstract:We consider minimizing a smooth function subject to a summation constraint over its variables. By exploiting a connection between the greedy 2-coordinate update for this problem and equality-constrained steepest descent in the 1-norm, we give a convergence rate for greedy selection under a proximal Polyak-Lojasiewicz assumption that is faster than random selection and independent of the problem dimension $n$. We then consider minimizing with both a summation constraint and bound constraints, as arises in the support vector machine dual problem. Existing greedy rules for this setting either guarantee trivial progress only or require $O(n^2)$ time to compute. We show that bound- and summation-constrained steepest descent in the L1-norm guarantees more progress per iteration than previous rules and can be computed in only $O(n \log n)$ time.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge