Chen Fan
Implicit Bias of SignGD and Adam on Multiclass Separable Data
Feb 07, 2025
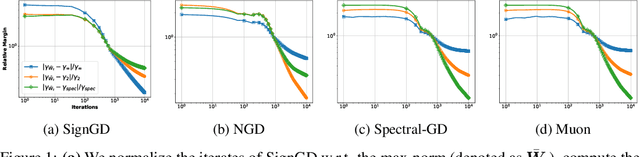
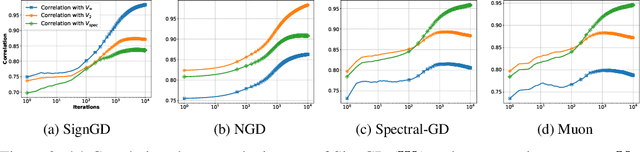
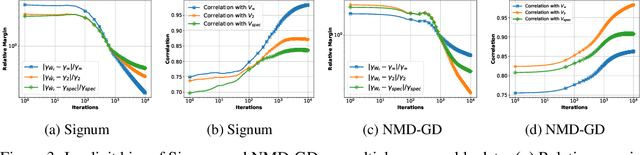
Abstract:In the optimization of overparameterized models, different gradient-based methods can achieve zero training error yet converge to distinctly different solutions inducing different generalization properties. While a decade of research on implicit optimization bias has illuminated this phenomenon in various settings, even the foundational case of linear classification with separable data still has important open questions. We resolve a fundamental gap by characterizing the implicit bias of both Adam and Sign Gradient Descent in multi-class cross-entropy minimization: we prove that their iterates converge to solutions that maximize the margin with respect to the classifier matrix's max-norm and characterize the rate of convergence. We extend our results to general p-norm normalized steepest descent algorithms and to other multi-class losses.
Enhancing Policy Gradient with the Polyak Step-Size Adaption
Apr 11, 2024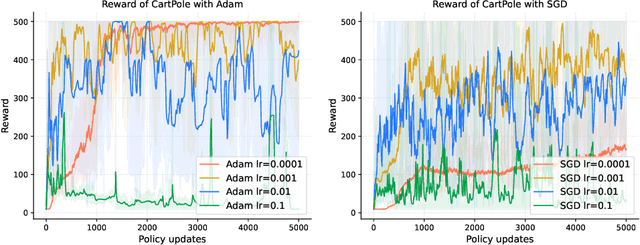
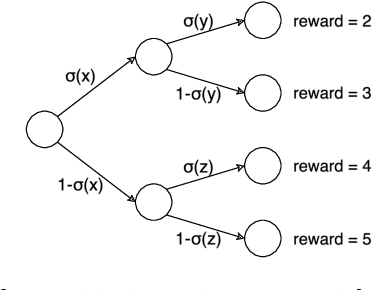
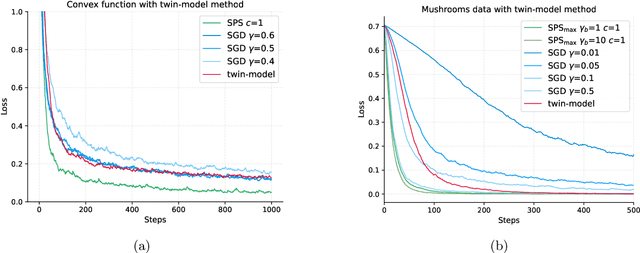
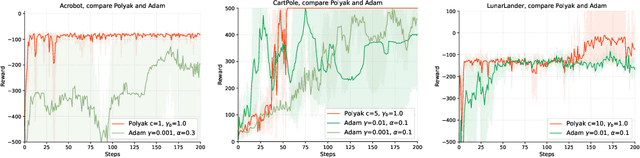
Abstract:Policy gradient is a widely utilized and foundational algorithm in the field of reinforcement learning (RL). Renowned for its convergence guarantees and stability compared to other RL algorithms, its practical application is often hindered by sensitivity to hyper-parameters, particularly the step-size. In this paper, we introduce the integration of the Polyak step-size in RL, which automatically adjusts the step-size without prior knowledge. To adapt this method to RL settings, we address several issues, including unknown f* in the Polyak step-size. Additionally, we showcase the performance of the Polyak step-size in RL through experiments, demonstrating faster convergence and the attainment of more stable policies.
BiSLS/SPS: Auto-tune Step Sizes for Stable Bi-level Optimization
May 30, 2023Abstract:The popularity of bi-level optimization (BO) in deep learning has spurred a growing interest in studying gradient-based BO algorithms. However, existing algorithms involve two coupled learning rates that can be affected by approximation errors when computing hypergradients, making careful fine-tuning necessary to ensure fast convergence. To alleviate this issue, we investigate the use of recently proposed adaptive step-size methods, namely stochastic line search (SLS) and stochastic Polyak step size (SPS), for computing both the upper and lower-level learning rates. First, we revisit the use of SLS and SPS in single-level optimization without the additional interpolation condition that is typically assumed in prior works. For such settings, we investigate new variants of SLS and SPS that improve upon existing suggestions in the literature and are simpler to implement. Importantly, these two variants can be seen as special instances of general family of methods with an envelope-type step-size. This unified envelope strategy allows for the extension of the algorithms and their convergence guarantees to BO settings. Finally, our extensive experiments demonstrate that the new algorithms, which are available in both SGD and Adam versions, can find large learning rates with minimal tuning and converge faster than corresponding vanilla SGD or Adam BO algorithms that require fine-tuning.
Fast Convergence of Random Reshuffling under Over-Parameterization and the Polyak-Łojasiewicz Condition
Apr 02, 2023Abstract:Modern machine learning models are often over-parameterized and as a result they can interpolate the training data. Under such a scenario, we study the convergence properties of a sampling-without-replacement variant of stochastic gradient descent (SGD) known as random reshuffling (RR). Unlike SGD that samples data with replacement at every iteration, RR chooses a random permutation of data at the beginning of each epoch and each iteration chooses the next sample from the permutation. For under-parameterized models, it has been shown RR can converge faster than SGD under certain assumptions. However, previous works do not show that RR outperforms SGD in over-parameterized settings except in some highly-restrictive scenarios. For the class of Polyak-\L ojasiewicz (PL) functions, we show that RR can outperform SGD in over-parameterized settings when either one of the following holds: (i) the number of samples ($n$) is less than the product of the condition number ($\kappa$) and the parameter ($\alpha$) of a weak growth condition (WGC), or (ii) $n$ is less than the parameter ($\rho$) of a strong growth condition (SGC).
FedBC: Calibrating Global and Local Models via Federated Learning Beyond Consensus
Jun 26, 2022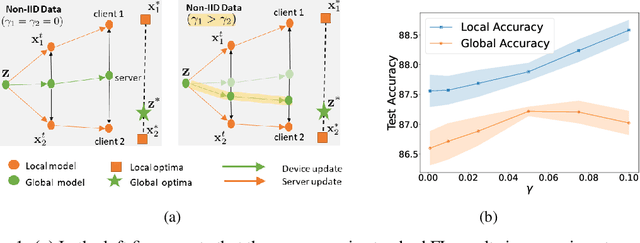
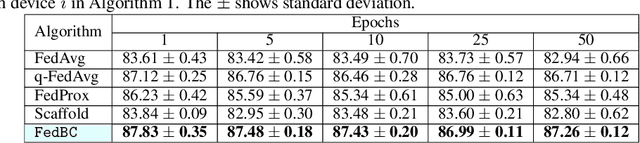
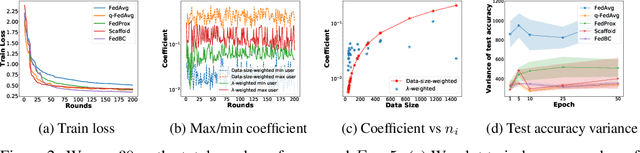
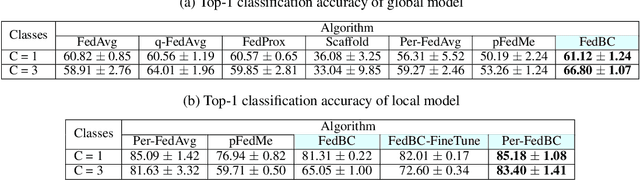
Abstract:In federated learning (FL), the objective of collaboratively learning a global model through aggregation of model updates across devices tends to oppose the goal of personalization via local information. In this work, we calibrate this tradeoff in a quantitative manner through a multi-criterion optimization-based framework, which we cast as a constrained program: the objective for a device is its local objective, which it seeks to minimize while satisfying nonlinear constraints that quantify the proximity between the local and the global model. By considering the Lagrangian relaxation of this problem, we develop an algorithm that allows each node to minimize its local component of Lagrangian through queries to a first-order gradient oracle. Then, the server executes Lagrange multiplier ascent steps followed by a Lagrange multiplier-weighted averaging step. We call this instantiation of the primal-dual method Federated Learning Beyond Consensus ($\texttt{FedBC}$). Theoretically, we establish that $\texttt{FedBC}$ converges to a first-order stationary point at rates that matches the state of the art, up to an additional error term that depends on the tolerance parameter that arises due to the proximity constraints. Overall, the analysis is a novel characterization of primal-dual methods applied to non-convex saddle point problems with nonlinear constraints. Finally, we demonstrate that $\texttt{FedBC}$ balances the global and local model test accuracy metrics across a suite of datasets (Synthetic, MNIST, CIFAR-10, Shakespeare), achieving competitive performance with the state of the art.
Sign-MAML: Efficient Model-Agnostic Meta-Learning by SignSGD
Sep 15, 2021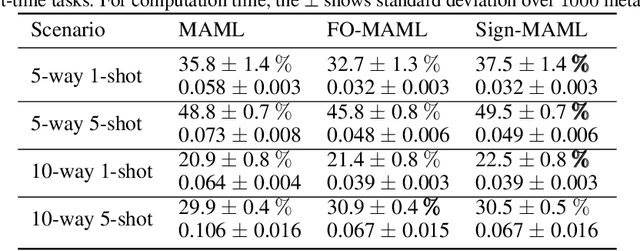
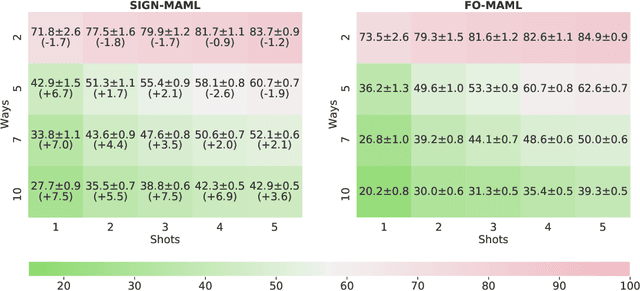
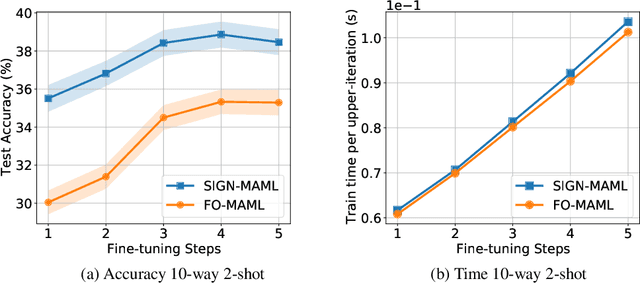
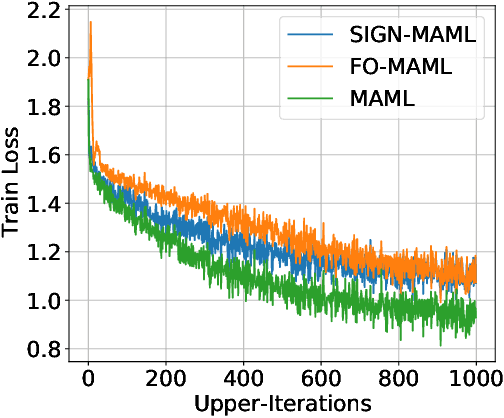
Abstract:We propose a new computationally-efficient first-order algorithm for Model-Agnostic Meta-Learning (MAML). The key enabling technique is to interpret MAML as a bilevel optimization (BLO) problem and leverage the sign-based SGD(signSGD) as a lower-level optimizer of BLO. We show that MAML, through the lens of signSGD-oriented BLO, naturally yields an alternating optimization scheme that just requires first-order gradients of a learned meta-model. We term the resulting MAML algorithm Sign-MAML. Compared to the conventional first-order MAML (FO-MAML) algorithm, Sign-MAML is theoretically-grounded as it does not impose any assumption on the absence of second-order derivatives during meta training. In practice, we show that Sign-MAML outperforms FO-MAML in various few-shot image classification tasks, and compared to MAML, it achieves a much more graceful tradeoff between classification accuracy and computation efficiency.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge