Rui Yuan
AlignTune: Modular Toolkit for Post-Training Alignment of Large Language Models
Feb 11, 2026Abstract:Post-training alignment is central to deploying large language models (LLMs), yet practical workflows remain split across backend-specific tools and ad-hoc glue code, making experiments hard to reproduce. We identify backend interference, reward fragmentation, and irreproducible pipelines as key obstacles in alignment research. We introduce AlignTune, a modular toolkit exposing a unified interface for supervised fine-tuning (SFT) and RLHF-style optimization with interchangeable TRL and Unsloth backends. AlignTune standardizes configuration, provides an extensible reward layer (rule-based and learned), and integrates evaluation over standard benchmarks and custom tasks. By isolating backend-specific logic behind a single factory boundary, AlignTune enables controlled comparisons and reproducible alignment experiments.
Beyond Uniform Credit: Causal Credit Assignment for Policy Optimization
Feb 10, 2026Abstract:Policy gradient methods for language model reasoning, such as GRPO and DAPO, assign uniform credit to all generated tokens - the filler phrase "Let me think" receives the same gradient update as the critical calculation "23 + 45 = 68." We propose counterfactual importance weighting: mask reasoning spans, measure the drop in answer probability, and upweight tokens accordingly during policy gradient updates. Our method requires no auxiliary models or external annotation, instead importance is estimated directly from the policy model's own probability shifts. Experiments on GSM8K across three models spanning the Qwen and Llama families demonstrate consistent improvements over uniform baselines and faster convergence to equivalent accuracy. Inverting the importance signal hurts performance, confirming we capture genuine causal structure rather than noise. Analysis shows the method correctly prioritizes calculation steps over scaffolding text. We view these findings as establishing counterfactual importance weighting as a foundation for further research rather than a complete solution.
Beyond KL Divergence: Policy Optimization with Flexible Bregman Divergences for LLM Reasoning
Feb 04, 2026Abstract:Policy optimization methods like Group Relative Policy Optimization (GRPO) and its variants have achieved strong results on mathematical reasoning and code generation tasks. Despite extensive exploration of reward processing strategies and training dynamics, all existing group-based methods exclusively use KL divergence for policy regularization, leaving the choice of divergence function unexplored. We introduce Group-Based Mirror Policy Optimization (GBMPO), a framework that extends group-based policy optimization to flexible Bregman divergences, including hand-designed alternatives (L2 in probability space) and learned neural mirror maps. On GSM8K mathematical reasoning, hand-designed ProbL2-GRPO achieves 86.7% accuracy, improving +5.5 points over the Dr. GRPO baseline. On MBPP code generation, neural mirror maps reach 60.1-60.8% pass@1, with random initialization already capturing most of the benefit. While evolutionary strategies meta-learning provides marginal accuracy improvements, its primary value lies in variance reduction ($\pm$0.2 versus $\pm$0.6) and efficiency gains (15% shorter responses on MBPP), suggesting that random initialization of neural mirror maps is sufficient for most practical applications. These results establish divergence choice as a critical, previously unexplored design dimension in group-based policy optimization for LLM reasoning.
A digital SRAM-based compute-in-memory macro for weight-stationary dynamic matrix multiplication in Transformer attention score computation
Nov 15, 2025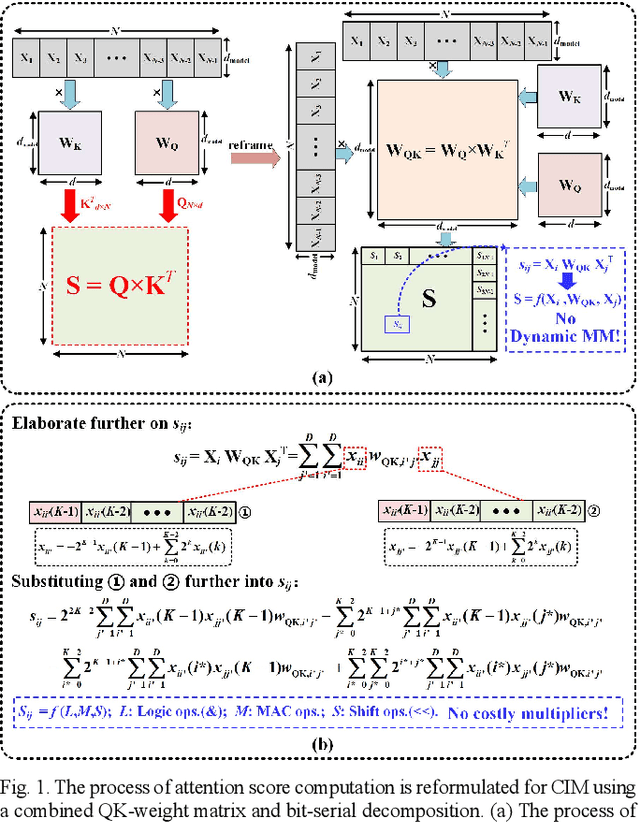
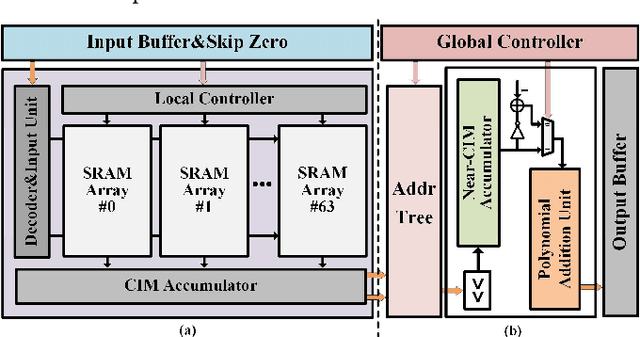


Abstract:Compute-in-memory (CIM) techniques are widely employed in energy-efficient artificial intelligent (AI) processors. They alleviate power and latency bottlenecks caused by extensive data movements between compute and storage units. This work proposes a digital CIM macro to compute Transformer attention. To mitigate dynamic matrix multiplication that is unsuitable for the common weight-stationary CIM paradigm, we reformulate the attention score computation process based on a combined QK-weight matrix, so that inputs can be directly fed to CIM cells to obtain the score results. Moreover, the involved binomial matrix multiplication operation is decomposed into 4 groups of bit-serial shifting and additions, without costly physical multipliers in the CIM. We maximize the energy efficiency of the CIM circuit through zero-value bit-skipping, data-driven word line activation, read-write separate 6T cells and bit-alternating 14T/28T adders. The proposed CIM macro was implemented using a 65-nm process. It occupied only 0.35 mm2 area, and delivered a 42.27 GOPS peak performance with 1.24 mW power consumption at a 1.0 V power supply and a 100 MHz clock frequency, resulting in 34.1 TOPS/W energy efficiency and 120.77 GOPS/mm2 area efficiency. When compared to the CPU and GPU, our CIM macro is 25x and 13x more energy efficient on practical tasks, respectively. Compared with other Transformer-CIMs, our design exhibits at least 7x energy efficiency and at least 2x area efficiency improvements when scaled to the same technology node, showcasing its potential for edge-side intelligent applications.
From predictions to confidence intervals: an empirical study of conformal prediction methods for in-context learning
Apr 22, 2025Abstract:Transformers have become a standard architecture in machine learning, demonstrating strong in-context learning (ICL) abilities that allow them to learn from the prompt at inference time. However, uncertainty quantification for ICL remains an open challenge, particularly in noisy regression tasks. This paper investigates whether ICL can be leveraged for distribution-free uncertainty estimation, proposing a method based on conformal prediction to construct prediction intervals with guaranteed coverage. While traditional conformal methods are computationally expensive due to repeated model fitting, we exploit ICL to efficiently generate confidence intervals in a single forward pass. Our empirical analysis compares this approach against ridge regression-based conformal methods, showing that conformal prediction with in-context learning (CP with ICL) achieves robust and scalable uncertainty estimates. Additionally, we evaluate its performance under distribution shifts and establish scaling laws to guide model training. These findings bridge ICL and conformal prediction, providing a theoretically grounded and new framework for uncertainty quantification in transformer-based models.
Rethinking Pseudo-Label Guided Learning for Weakly Supervised Temporal Action Localization from the Perspective of Noise Correction
Jan 19, 2025



Abstract:Pseudo-label learning methods have been widely applied in weakly-supervised temporal action localization. Existing works directly utilize weakly-supervised base model to generate instance-level pseudo-labels for training the fully-supervised detection head. We argue that the noise in pseudo-labels would interfere with the learning of fully-supervised detection head, leading to significant performance leakage. Issues with noisy labels include:(1) inaccurate boundary localization; (2) undetected short action clips; (3) multiple adjacent segments incorrectly detected as one segment. To target these issues, we introduce a two-stage noisy label learning strategy to harness every potential useful signal in noisy labels. First, we propose a frame-level pseudo-label generation model with a context-aware denoising algorithm to refine the boundaries. Second, we introduce an online-revised teacher-student framework with a missing instance compensation module and an ambiguous instance correction module to solve the short-action-missing and many-to-one problems. Besides, we apply a high-quality pseudo-label mining loss in our online-revised teacher-student framework to add different weights to the noisy labels to train more effectively. Our model outperforms the previous state-of-the-art method in detection accuracy and inference speed greatly upon the THUMOS14 and ActivityNet v1.2 benchmarks.
Hunyuan-Large: An Open-Source MoE Model with 52 Billion Activated Parameters by Tencent
Nov 05, 2024
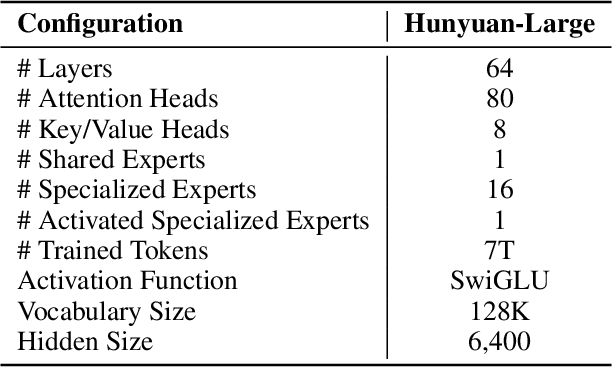
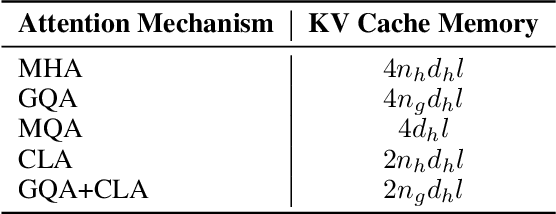
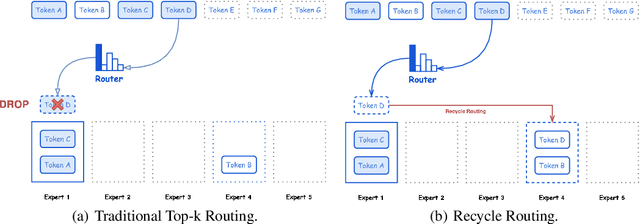
Abstract:In this paper, we introduce Hunyuan-Large, which is currently the largest open-source Transformer-based mixture of experts model, with a total of 389 billion parameters and 52 billion activation parameters, capable of handling up to 256K tokens. We conduct a thorough evaluation of Hunyuan-Large's superior performance across various benchmarks including language understanding and generation, logical reasoning, mathematical problem-solving, coding, long-context, and aggregated tasks, where it outperforms LLama3.1-70B and exhibits comparable performance when compared to the significantly larger LLama3.1-405B model. Key practice of Hunyuan-Large include large-scale synthetic data that is orders larger than in previous literature, a mixed expert routing strategy, a key-value cache compression technique, and an expert-specific learning rate strategy. Additionally, we also investigate the scaling laws and learning rate schedule of mixture of experts models, providing valuable insights and guidances for future model development and optimization. The code and checkpoints of Hunyuan-Large are released to facilitate future innovations and applications. Codes: https://github.com/Tencent/Hunyuan-Large Models: https://huggingface.co/tencent/Tencent-Hunyuan-Large
Enhancing Policy Gradient with the Polyak Step-Size Adaption
Apr 11, 2024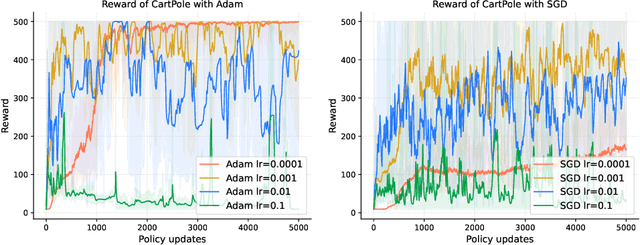
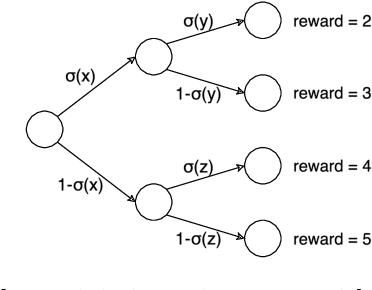
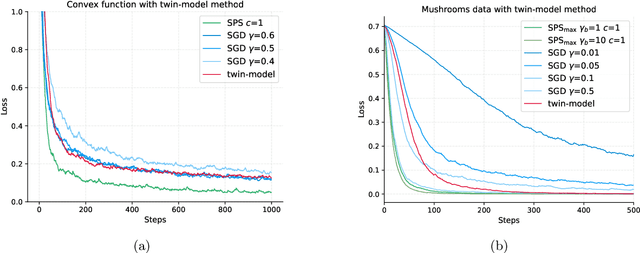
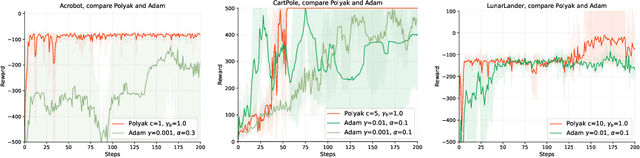
Abstract:Policy gradient is a widely utilized and foundational algorithm in the field of reinforcement learning (RL). Renowned for its convergence guarantees and stability compared to other RL algorithms, its practical application is often hindered by sensitivity to hyper-parameters, particularly the step-size. In this paper, we introduce the integration of the Polyak step-size in RL, which automatically adjusts the step-size without prior knowledge. To adapt this method to RL settings, we address several issues, including unknown f* in the Polyak step-size. Additionally, we showcase the performance of the Polyak step-size in RL through experiments, demonstrating faster convergence and the attainment of more stable policies.
A New Time Series Similarity Measure and Its Smart Grid Applications
Oct 19, 2023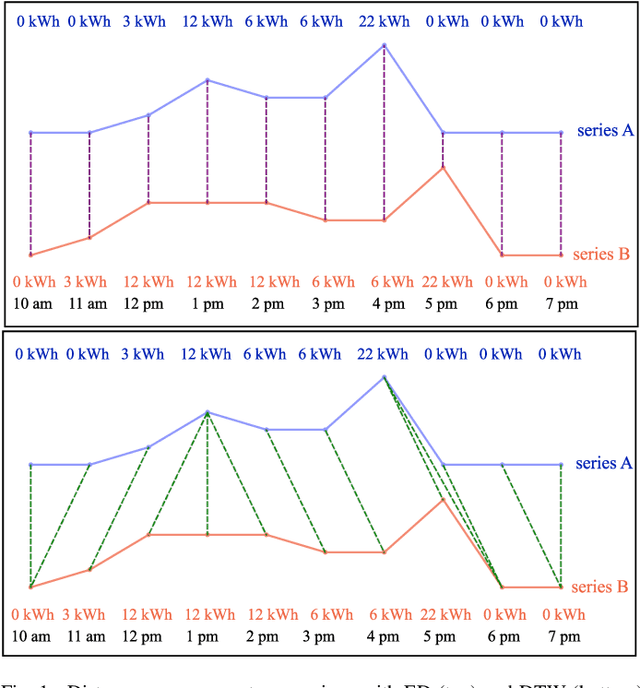
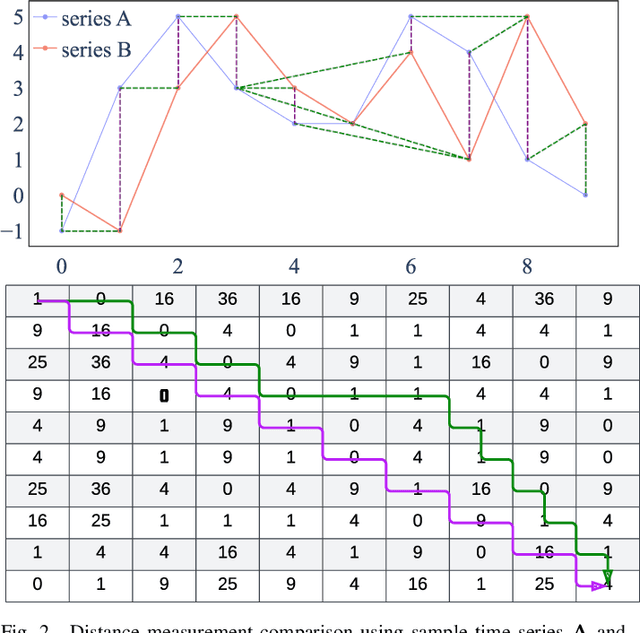
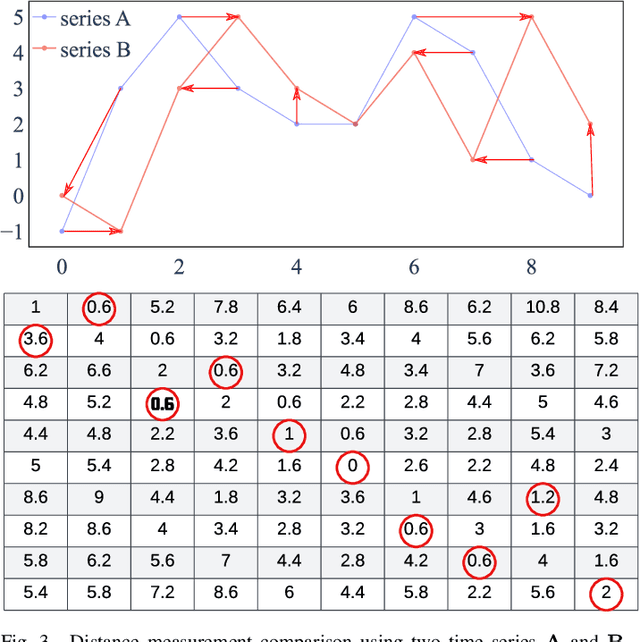
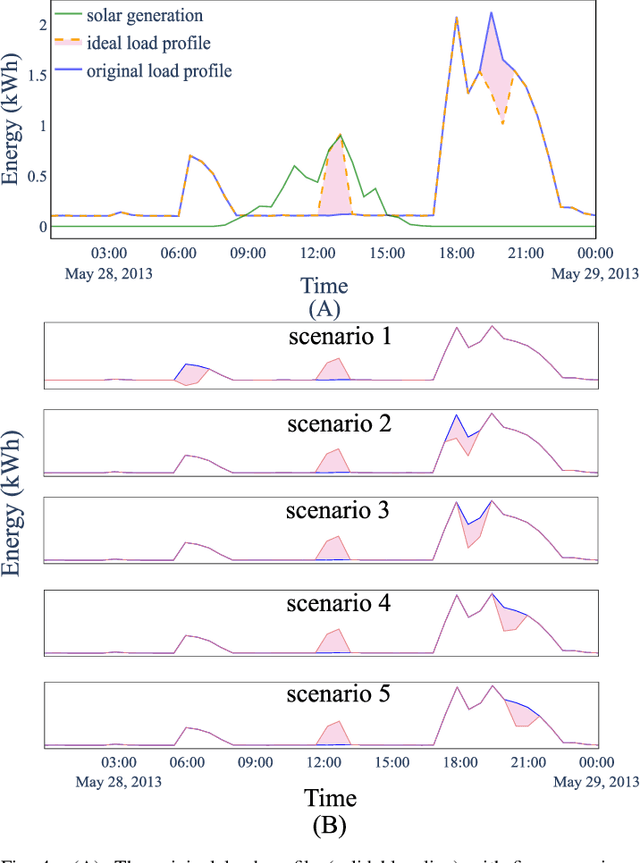
Abstract:Many smart grid applications involve data mining, clustering, classification, identification, and anomaly detection, among others. These applications primarily depend on the measurement of similarity, which is the distance between different time series or subsequences of a time series. The commonly used time series distance measures, namely Euclidean Distance (ED) and Dynamic Time Warping (DTW), do not quantify the flexible nature of electricity usage data in terms of temporal dynamics. As a result, there is a need for a new distance measure that can quantify both the amplitude and temporal changes of electricity time series for smart grid applications, e.g., demand response and load profiling. This paper introduces a novel distance measure to compare electricity usage patterns. The method consists of two phases that quantify the effort required to reshape one time series into another, considering both amplitude and temporal changes. The proposed method is evaluated against ED and DTW using real-world data in three smart grid applications. Overall, the proposed measure outperforms ED and DTW in accurately identifying the best load scheduling strategy, anomalous days with irregular electricity usage, and determining electricity users' behind-the-meter (BTM) equipment.
A Novel Framework for Policy Mirror Descent with General Parametrization and Linear Convergence
Jan 30, 2023

Abstract:Modern policy optimization methods in applied reinforcement learning are often inspired by the trust region policy optimization algorithm, which can be interpreted as a particular instance of policy mirror descent. While theoretical guarantees have been established for this framework, particularly in the tabular setting, the use of a general parametrization scheme remains mostly unjustified. In this work, we introduce a novel framework for policy optimization based on mirror descent that naturally accommodates general parametrizations. The policy class induced by our scheme recovers known classes, e.g. tabular softmax, log-linear, and neural policies. It also generates new ones, depending on the choice of the mirror map. For a general mirror map and parametrization function, we establish the quasi-monotonicity of the updates in value function, global linear convergence rates, and we bound the total variation of the algorithm along its path. To showcase the ability of our framework to accommodate general parametrization schemes, we present a case study involving shallow neural networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge