Linear Convergence of Natural Policy Gradient Methods with Log-Linear Policies
Paper and Code
Oct 04, 2022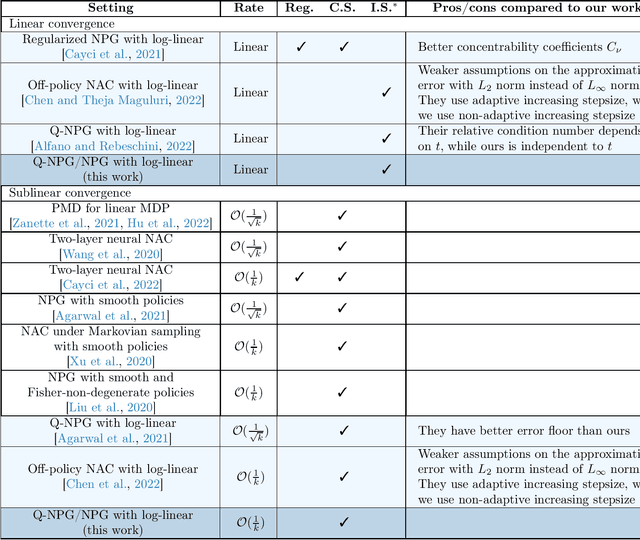
We consider infinite-horizon discounted Markov decision processes and study the convergence rates of the natural policy gradient (NPG) and the Q-NPG methods with the log-linear policy class. Using the compatible function approximation framework, both methods with log-linear policies can be written as approximate versions of the policy mirror descent (PMD) method. We show that both methods attain linear convergence rates and $\mathcal{O}(1/\epsilon^2)$ sample complexities using a simple, non-adaptive geometrically increasing step size, without resorting to entropy or other strongly convex regularization. Lastly, as a byproduct, we obtain sublinear convergence rates for both methods with arbitrary constant step size.
View paper on
 OpenReview
OpenReview
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge