Scaling Laws for Uncertainty in Deep Learning

Deep learning has recently revealed the existence of scaling laws, demonstrating that model performance follows predictable trends based on dataset and model sizes. Inspired by these findings and fascinating phenomena emerging in the over-parameterized regime, we examine a parallel direction: do similar scaling laws govern predictive uncertainties in deep learning? In identifiable parametric models, such scaling laws can be derived in a straightforward manner by treating model parameters in a Bayesian way. In this case, for example, we obtain $O(1/N)$ contraction rates for epistemic uncertainty with respect to the number of data $N$. However, in over-parameterized models, these guarantees do not hold, leading to largely unexplored behaviors. In this work, we empirically show the existence of scaling laws associated with various measures of predictive uncertainty with respect to dataset and model sizes. Through experiments on vision and language tasks, we observe such scaling laws for in- and out-of-distribution predictive uncertainty estimated through popular approximate Bayesian inference and ensemble methods. Besides the elegance of scaling laws and the practical utility of extrapolating uncertainties to larger data or models, this work provides strong evidence to dispel recurring skepticism against Bayesian approaches: "In many applications of deep learning we have so much data available: what do we need Bayes for?". Our findings show that "so much data" is typically not enough to make epistemic uncertainty negligible.

From predictions to confidence intervals: an empirical study of conformal prediction methods for in-context learning

Transformers have become a standard architecture in machine learning, demonstrating strong in-context learning (ICL) abilities that allow them to learn from the prompt at inference time. However, uncertainty quantification for ICL remains an open challenge, particularly in noisy regression tasks. This paper investigates whether ICL can be leveraged for distribution-free uncertainty estimation, proposing a method based on conformal prediction to construct prediction intervals with guaranteed coverage. While traditional conformal methods are computationally expensive due to repeated model fitting, we exploit ICL to efficiently generate confidence intervals in a single forward pass. Our empirical analysis compares this approach against ridge regression-based conformal methods, showing that conformal prediction with in-context learning (CP with ICL) achieves robust and scalable uncertainty estimates. Additionally, we evaluate its performance under distribution shifts and establish scaling laws to guide model training. These findings bridge ICL and conformal prediction, providing a theoretically grounded and new framework for uncertainty quantification in transformer-based models.

Think2SQL: Reinforce LLM Reasoning Capabilities for Text2SQL

Large Language Models (LLMs) have shown impressive capabilities in transforming natural language questions about relational databases into SQL queries. Despite recent improvements, small LLMs struggle to handle questions involving multiple tables and complex SQL patterns under a Zero-Shot Learning (ZSL) setting. Supervised Fine-Tuning (SFT) partially compensate the knowledge deficits in pretrained models but falls short while dealing with queries involving multi-hop reasoning. To bridge this gap, different LLM training strategies to reinforce reasoning capabilities have been proposed, ranging from leveraging a thinking process within ZSL, including reasoning traces in SFT, or adopt Reinforcement Learning (RL) strategies. However, the influence of reasoning on Text2SQL performance is still largely unexplored. This paper investigates to what extent LLM reasoning capabilities influence their Text2SQL performance on four benchmark datasets. To this end, it considers the following LLM settings: (1) ZSL, including general-purpose reasoning or not; (2) SFT, with and without task-specific reasoning traces; (3) RL, leveraging execution accuracy as primary reward function; (4) SFT+RL, i.e, a two-stage approach that combines SFT and RL. The results show that general-purpose reasoning under ZSL proves to be ineffective in tackling complex Text2SQL cases. Small LLMs benefit from SFT with reasoning much more than larger ones, bridging the gap of their (weaker) model pretraining. RL is generally beneficial across all tested models and datasets, particularly when SQL queries involve multi-hop reasoning and multiple tables. Small LLMs with SFT+RL excel on most complex datasets thanks to a strategic balance between generality of the reasoning process and optimization of the execution accuracy. Thanks to RL, the7B Qwen-Coder-2.5 model performs on par with 100+ Billion ones on the Bird dataset.

Optimizing Diffusion Models for Joint Trajectory Prediction and Controllable Generation

Diffusion models are promising for joint trajectory prediction and controllable generation in autonomous driving, but they face challenges of inefficient inference steps and high computational demands. To tackle these challenges, we introduce Optimal Gaussian Diffusion (OGD) and Estimated Clean Manifold (ECM) Guidance. OGD optimizes the prior distribution for a small diffusion time $T$ and starts the reverse diffusion process from it. ECM directly injects guidance gradients to the estimated clean manifold, eliminating extensive gradient backpropagation throughout the network. Our methodology streamlines the generative process, enabling practical applications with reduced computational overhead. Experimental validation on the large-scale Argoverse 2 dataset demonstrates our approach's superior performance, offering a viable solution for computationally efficient, high-quality joint trajectory prediction and controllable generation for autonomous driving. Our project webpage is at https://yixiaowang7.github.io/OptTrajDiff_Page/.

Class Balanced Dynamic Acquisition for Domain Adaptive Semantic Segmentation using Active Learning

Domain adaptive active learning is leading the charge in label-efficient training of neural networks. For semantic segmentation, state-of-the-art models jointly use two criteria of uncertainty and diversity to select training labels, combined with a pixel-wise acquisition strategy. However, we show that such methods currently suffer from a class imbalance issue which degrades their performance for larger active learning budgets. We then introduce Class Balanced Dynamic Acquisition (CBDA), a novel active learning method that mitigates this issue, especially in high-budget regimes. The more balanced labels increase minority class performance, which in turn allows the model to outperform the previous baseline by 0.6, 1.7, and 2.4 mIoU for budgets of 5%, 10%, and 20%, respectively. Additionally, the focus on minority classes leads to improvements of the minimum class performance of 0.5, 2.9, and 4.6 IoU respectively. The top-performing model even exceeds the fully supervised baseline, showing that a more balanced label than the entire ground truth can be beneficial.

On permutation symmetries in Bayesian neural network posteriors: a variational perspective

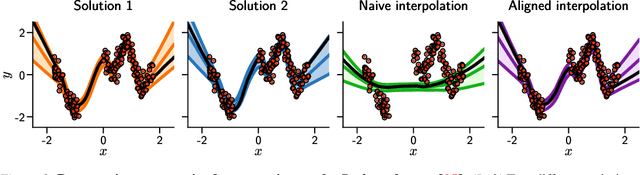
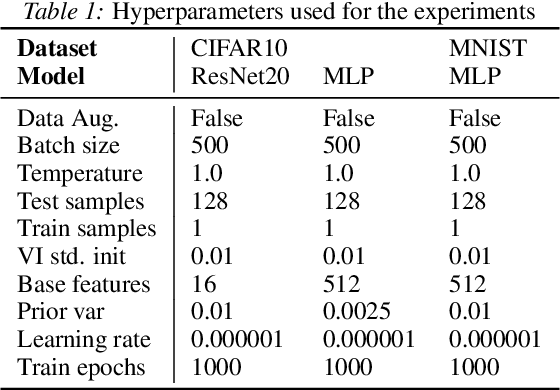
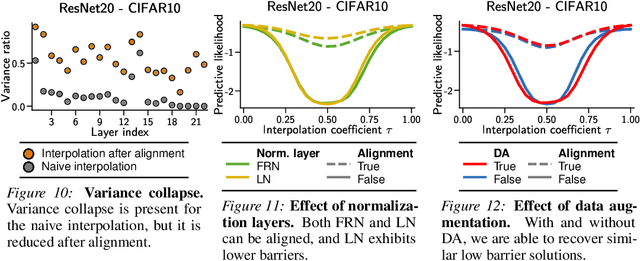
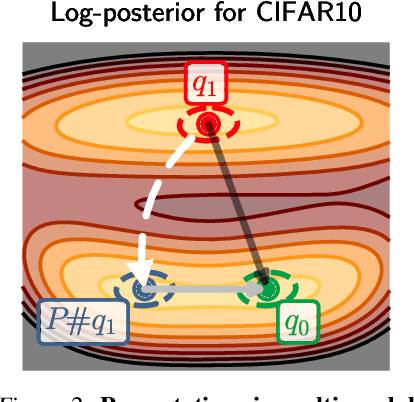
The elusive nature of gradient-based optimization in neural networks is tied to their loss landscape geometry, which is poorly understood. However recent work has brought solid evidence that there is essentially no loss barrier between the local solutions of gradient descent, once accounting for weight-permutations that leave the network's computation unchanged. This raises questions for approximate inference in Bayesian neural networks (BNNs), where we are interested in marginalizing over multiple points in the loss landscape. In this work, we first extend the formalism of marginalized loss barrier and solution interpolation to BNNs, before proposing a matching algorithm to search for linearly connected solutions. This is achieved by aligning the distributions of two independent approximate Bayesian solutions with respect to permutation matrices. We build on the results of Ainsworth et al. (2023), reframing the problem as a combinatorial optimization one, using an approximation to the sum of bilinear assignment problem. We then experiment on a variety of architectures and datasets, finding nearly zero marginalized loss barriers for linearly connected solutions.

Continuous-Time Functional Diffusion Processes

We introduce functional diffusion processes (FDPs), which generalize traditional score-based diffusion models to infinite-dimensional function spaces. FDPs require a new mathematical framework to describe the forward and backward dynamics, and several extensions to derive practical training objectives. These include infinite-dimensional versions of the Girsanov theorem, in order to be able to compute an ELBO, and of the sampling theorem, in order to guarantee that functional evaluations in a countable set of points are equivalent to infinite-dimensional functions. We use FDPs to build a new breed of generative models in function spaces, which do not require specialized network architectures, and that can work with any kind of continuous data. Our results on synthetic and real data illustrate the advantages of FDPs in simplifying the design requirements of diffusion models.

How Much is Enough? A Study on Diffusion Times in Score-based Generative Models

Score-based diffusion models are a class of generative models whose dynamics is described by stochastic differential equations that map noise into data. While recent works have started to lay down a theoretical foundation for these models, an analytical understanding of the role of the diffusion time T is still lacking. Current best practice advocates for a large T to ensure that the forward dynamics brings the diffusion sufficiently close to a known and simple noise distribution; however, a smaller value of T should be preferred for a better approximation of the score-matching objective and higher computational efficiency. Starting from a variational interpretation of diffusion models, in this work we quantify this trade-off, and suggest a new method to improve quality and efficiency of both training and sampling, by adopting smaller diffusion times. Indeed, we show how an auxiliary model can be used to bridge the gap between the ideal and the simulated forward dynamics, followed by a standard reverse diffusion process. Empirical results support our analysis; for image data, our method is competitive w.r.t. the state-of-the-art, according to standard sample quality metrics and log-likelihood.

Model Selection for Bayesian Autoencoders

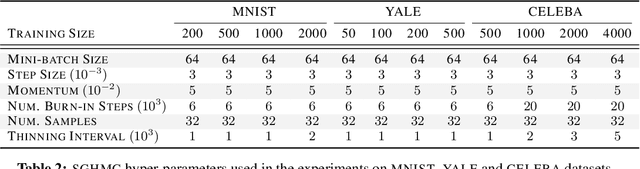
We develop a novel method for carrying out model selection for Bayesian autoencoders (BAEs) by means of prior hyper-parameter optimization. Inspired by the common practice of type-II maximum likelihood optimization and its equivalence to Kullback-Leibler divergence minimization, we propose to optimize the distributional sliced-Wasserstein distance (DSWD) between the output of the autoencoder and the empirical data distribution. The advantages of this formulation are that we can estimate the DSWD based on samples and handle high-dimensional problems. We carry out posterior estimation of the BAE parameters via stochastic gradient Hamiltonian Monte Carlo and turn our BAE into a generative model by fitting a flexible Dirichlet mixture model in the latent space. Consequently, we obtain a powerful alternative to variational autoencoders, which are the preferred choice in modern applications of autoencoders for representation learning with uncertainty. We evaluate our approach qualitatively and quantitatively using a vast experimental campaign on a number of unsupervised learning tasks and show that, in small-data regimes where priors matter, our approach provides state-of-the-art results, outperforming multiple competitive baselines.

Enhancing human bodies with extra robotic arms and fingers: The Neural Resource Allocation Problem

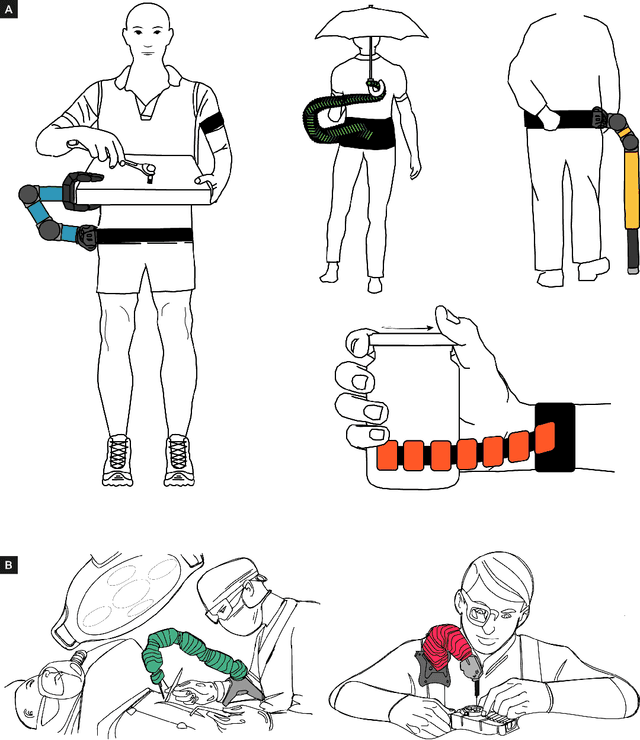
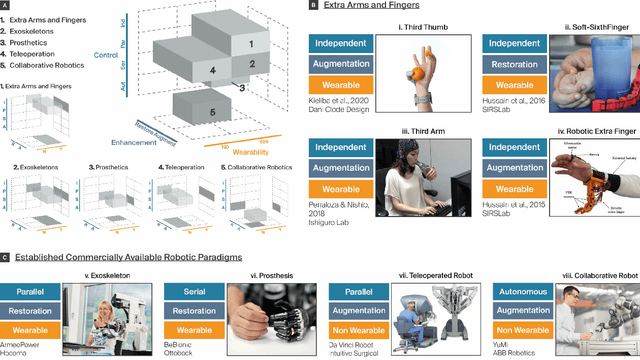
The emergence of robot-based body augmentation promises exciting innovations that will inform robotics, human-machine interaction, and wearable electronics. Even though augmentative devices like extra robotic arms and fingers in many ways build on restorative technologies, they introduce unique challenges for bidirectional human-machine collaboration. Can humans adapt and learn to operate a new limb collaboratively with their biological limbs without sacrificing their physical abilities? To successfully achieve robotic body augmentation, we need to ensure that by giving a person an additional (artificial) limb, we are not in fact trading off an existing (biological) one. In this manuscript, we introduce the "Neural Resource Allocation" problem, which distinguishes body augmentation from existing robotics paradigms such as teleoperation and prosthetics. We discuss how to allow the effective and effortless voluntary control of augmentative devices without compromising the voluntary control of the biological body. In reviewing the relevant literature on extra robotic fingers and limbs we critically assess the range of potential solutions available for the "Neural Resource Allocation" problem. For this purpose, we combine multiple perspectives from engineering and neuroscience with considerations from human-machine interaction, sensory-motor integration, ethics and law. Altogether we aim to define common foundations and operating principles for the successful implementation of motor augmentation.