Robust Classification by Coupling Data Mollification with Label Smoothing

Introducing training-time augmentations is a key technique to enhance generalization and prepare deep neural networks against test-time corruptions. Inspired by the success of generative diffusion models, we propose a novel approach coupling data augmentation, in the form of image noising and blurring, with label smoothing to align predicted label confidences with image degradation. The method is simple to implement, introduces negligible overheads, and can be combined with existing augmentations. We demonstrate improved robustness and uncertainty quantification on the corrupted image benchmarks of the CIFAR and TinyImageNet datasets.

BOLD: Boolean Logic Deep Learning

Deep learning is computationally intensive, with significant efforts focused on reducing arithmetic complexity, particularly regarding energy consumption dominated by data movement. While existing literature emphasizes inference, training is considerably more resource-intensive. This paper proposes a novel mathematical principle by introducing the notion of Boolean variation such that neurons made of Boolean weights and inputs can be trained -- for the first time -- efficiently in Boolean domain using Boolean logic instead of gradient descent and real arithmetic. We explore its convergence, conduct extensively experimental benchmarking, and provide consistent complexity evaluation by considering chip architecture, memory hierarchy, dataflow, and arithmetic precision. Our approach achieves baseline full-precision accuracy in ImageNet classification and surpasses state-of-the-art results in semantic segmentation, with notable performance in image super-resolution, and natural language understanding with transformer-based models. Moreover, it significantly reduces energy consumption during both training and inference.

Spatial Bayesian Neural Networks

Statistical models for spatial processes play a central role in statistical analyses of spatial data. Yet, it is the simple, interpretable, and well understood models that are routinely employed even though, as is revealed through prior and posterior predictive checks, these can poorly characterise the spatial heterogeneity in the underlying process of interest. Here, we propose a new, flexible class of spatial-process models, which we refer to as spatial Bayesian neural networks (SBNNs). An SBNN leverages the representational capacity of a Bayesian neural network; it is tailored to a spatial setting by incorporating a spatial "embedding layer" into the network and, possibly, spatially-varying network parameters. An SBNN is calibrated by matching its finite-dimensional distribution at locations on a fine gridding of space to that of a target process of interest. That process could be easy to simulate from or we have many realisations from it. We propose several variants of SBNNs, most of which are able to match the finite-dimensional distribution of the target process at the selected grid better than conventional BNNs of similar complexity. We also show that a single SBNN can be used to represent a variety of spatial processes often used in practice, such as Gaussian processes and lognormal processes. We briefly discuss the tools that could be used to make inference with SBNNs, and we conclude with a discussion of their advantages and limitations.

One-Line-of-Code Data Mollification Improves Optimization of Likelihood-based Generative Models

Generative Models (GMs) have attracted considerable attention due to their tremendous success in various domains, such as computer vision where they are capable to generate impressive realistic-looking images. Likelihood-based GMs are attractive due to the possibility to generate new data by a single model evaluation. However, they typically achieve lower sample quality compared to state-of-the-art score-based diffusion models (DMs). This paper provides a significant step in the direction of addressing this limitation. The idea is to borrow one of the strengths of score-based DMs, which is the ability to perform accurate density estimation in low-density regions and to address manifold overfitting by means of data mollification. We connect data mollification through the addition of Gaussian noise to Gaussian homotopy, which is a well-known technique to improve optimization. Data mollification can be implemented by adding one line of code in the optimization loop, and we demonstrate that this provides a boost in generation quality of likelihood-based GMs, without computational overheads. We report results on image data sets with popular likelihood-based GMs, including variants of variational autoencoders and normalizing flows, showing large improvements in FID score.

Fully Bayesian Autoencoders with Latent Sparse Gaussian Processes

Autoencoders and their variants are among the most widely used models in representation learning and generative modeling. However, autoencoder-based models usually assume that the learned representations are i.i.d. and fail to capture the correlations between the data samples. To address this issue, we propose a novel Sparse Gaussian Process Bayesian Autoencoder (SGPBAE) model in which we impose fully Bayesian sparse Gaussian Process priors on the latent space of a Bayesian Autoencoder. We perform posterior estimation for this model via stochastic gradient Hamiltonian Monte Carlo. We evaluate our approach qualitatively and quantitatively on a wide range of representation learning and generative modeling tasks and show that our approach consistently outperforms multiple alternatives relying on Variational Autoencoders.

Model Selection for Bayesian Autoencoders

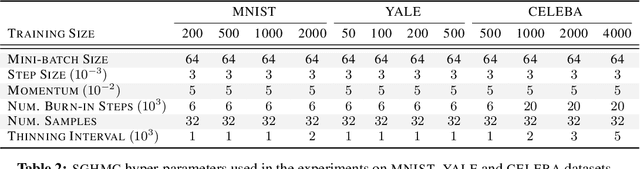
We develop a novel method for carrying out model selection for Bayesian autoencoders (BAEs) by means of prior hyper-parameter optimization. Inspired by the common practice of type-II maximum likelihood optimization and its equivalence to Kullback-Leibler divergence minimization, we propose to optimize the distributional sliced-Wasserstein distance (DSWD) between the output of the autoencoder and the empirical data distribution. The advantages of this formulation are that we can estimate the DSWD based on samples and handle high-dimensional problems. We carry out posterior estimation of the BAE parameters via stochastic gradient Hamiltonian Monte Carlo and turn our BAE into a generative model by fitting a flexible Dirichlet mixture model in the latent space. Consequently, we obtain a powerful alternative to variational autoencoders, which are the preferred choice in modern applications of autoencoders for representation learning with uncertainty. We evaluate our approach qualitatively and quantitatively using a vast experimental campaign on a number of unsupervised learning tasks and show that, in small-data regimes where priors matter, our approach provides state-of-the-art results, outperforming multiple competitive baselines.

All You Need is a Good Functional Prior for Bayesian Deep Learning

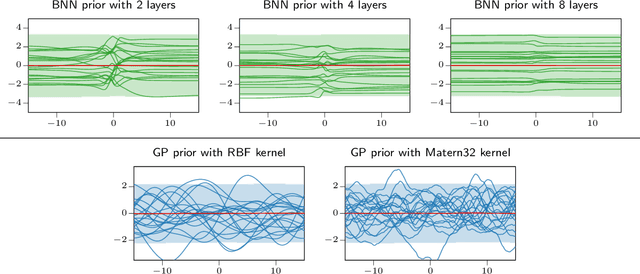
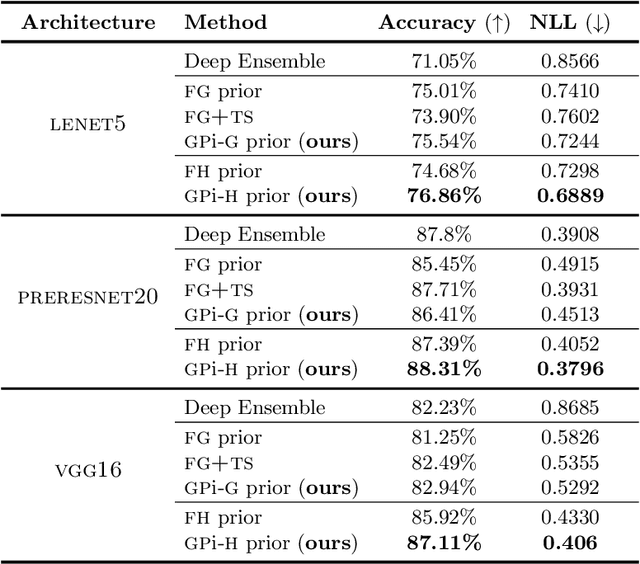
The Bayesian treatment of neural networks dictates that a prior distribution is specified over their weight and bias parameters. This poses a challenge because modern neural networks are characterized by a large number of parameters, and the choice of these priors has an uncontrolled effect on the induced functional prior, which is the distribution of the functions obtained by sampling the parameters from their prior distribution. We argue that this is a hugely limiting aspect of Bayesian deep learning, and this work tackles this limitation in a practical and effective way. Our proposal is to reason in terms of functional priors, which are easier to elicit, and to "tune" the priors of neural network parameters in a way that they reflect such functional priors. Gaussian processes offer a rigorous framework to define prior distributions over functions, and we propose a novel and robust framework to match their prior with the functional prior of neural networks based on the minimization of their Wasserstein distance. We provide vast experimental evidence that coupling these priors with scalable Markov chain Monte Carlo sampling offers systematically large performance improvements over alternative choices of priors and state-of-the-art approximate Bayesian deep learning approaches. We consider this work a considerable step in the direction of making the long-standing challenge of carrying out a fully Bayesian treatment of neural networks, including convolutional neural networks, a concrete possibility.