Spatio-temporal modeling and forecasting with Fourier neural operators

Spatio-temporal process models are often used for modeling dynamic physical and biological phenomena that evolve across space and time. These phenomena may exhibit environmental heterogeneity and complex interactions that are difficult to capture using traditional statistical process models such as Gaussian processes. This work proposes the use of Fourier neural operators (FNOs) for constructing statistical dynamical spatio-temporal models for forecasting. An FNO is a flexible mapping of functions that approximates the solution operator of possibly unknown linear or non-linear partial differential equations (PDEs) in a computationally efficient manner. It does so using samples of inputs and their respective outputs, and hence explicit knowledge of the underlying PDE is not required. Through simulations from a nonlinear PDE with known solution, we compare FNO forecasts to those from state-of-the-art statistical spatio-temporal-forecasting methods. Further, using sea surface temperature data over the Atlantic Ocean and precipitation data across Europe, we demonstrate the ability of FNO-based dynamic spatio-temporal (DST) statistical modeling to capture complex real-world spatio-temporal dependencies. Using collections of testing instances, we show that the FNO-DST forecasts are accurate with valid uncertainty quantification.

Modeling nonstationary spatial processes with normalizing flows

Nonstationary spatial processes can often be represented as stationary processes on a warped spatial domain. Selecting an appropriate spatial warping function for a given application is often difficult and, as a result of this, warping methods have largely been limited to two-dimensional spatial domains. In this paper, we introduce a novel approach to modeling nonstationary, anisotropic spatial processes using neural autoregressive flows (NAFs), a class of invertible mappings capable of generating complex, high-dimensional warpings. Through simulation studies we demonstrate that a NAF-based model has greater representational capacity than other commonly used spatial process models. We apply our proposed modeling framework to a subset of the 3D Argo Floats dataset, highlighting the utility of our framework in real-world applications.

Neural Conditional Simulation for Complex Spatial Processes

A key objective in spatial statistics is to simulate from the distribution of a spatial process at a selection of unobserved locations conditional on observations (i.e., a predictive distribution) to enable spatial prediction and uncertainty quantification. However, exact conditional simulation from this predictive distribution is intractable or inefficient for many spatial process models. In this paper, we propose neural conditional simulation (NCS), a general method for spatial conditional simulation that is based on neural diffusion models. Specifically, using spatial masks, we implement a conditional score-based diffusion model that evolves Gaussian noise into samples from a predictive distribution when given a partially observed spatial field and spatial process parameters as inputs. The diffusion model relies on a neural network that only requires unconditional samples from the spatial process for training. Once trained, the diffusion model is amortized with respect to the observations in the partially observed field, the number and locations of those observations, and the spatial process parameters, and can therefore be used to conditionally simulate from a broad class of predictive distributions without retraining the neural network. We assess the NCS-generated simulations against simulations from the true conditional distribution of a Gaussian process model, and against Markov chain Monte Carlo (MCMC) simulations from a Brown--Resnick process model for spatial extremes. In the latter case, we show that it is more efficient and accurate to conditionally simulate using NCS than classical MCMC techniques implemented in standard software. We conclude that NCS enables efficient and accurate conditional simulation from spatial predictive distributions that are challenging to sample from using traditional methods.

Neural Parameter Estimation with Incomplete Data

Advancements in artificial intelligence (AI) and deep learning have led to neural networks being used to generate lightning-speed answers to complex questions, to paint like Monet, or to write like Proust. Leveraging their computational speed and flexibility, neural networks are also being used to facilitate fast, likelihood-free statistical inference. However, it is not straightforward to use neural networks with data that for various reasons are incomplete, which precludes their use in many applications. A recently proposed approach to remedy this issue inputs an appropriately padded data vector and a vector that encodes the missingness pattern to a neural network. While computationally efficient, this "masking" approach can result in statistically inefficient inferences. Here, we propose an alternative approach that is based on the Monte Carlo expectation-maximization (EM) algorithm. Our EM approach is likelihood-free, substantially faster than the conventional EM algorithm as it does not require numerical optimization at each iteration, and more statistically efficient than the masking approach. This research represents a prototype problem that indicates how improvements could be made in AI by introducing Bayesian statistical thinking. We compare the two approaches to missingness using simulated incomplete data from two models: a spatial Gaussian process model, and a spatial Potts model. The utility of the methodology is shown on Arctic sea-ice data and cryptocurrency data.

Neural Methods for Amortised Parameter Inference

Simulation-based methods for making statistical inference have evolved dramatically over the past 50 years, keeping pace with technological advancements. The field is undergoing a new revolution as it embraces the representational capacity of neural networks, optimisation libraries, and graphics processing units for learning complex mappings between data and inferential targets. The resulting tools are amortised, in the sense that they allow inference to be made quickly through fast feedforward operations. In this article we review recent progress made in the context of point estimation, approximate Bayesian inference, the automatic construction of summary statistics, and likelihood approximation. The review also covers available software, and includes a simple illustration to showcase the wide array of tools available for amortised inference and the benefits they offer over state-of-the-art Markov chain Monte Carlo methods. The article concludes with an overview of relevant topics and an outlook on future research directions.

Spatial Bayesian Neural Networks

Statistical models for spatial processes play a central role in statistical analyses of spatial data. Yet, it is the simple, interpretable, and well understood models that are routinely employed even though, as is revealed through prior and posterior predictive checks, these can poorly characterise the spatial heterogeneity in the underlying process of interest. Here, we propose a new, flexible class of spatial-process models, which we refer to as spatial Bayesian neural networks (SBNNs). An SBNN leverages the representational capacity of a Bayesian neural network; it is tailored to a spatial setting by incorporating a spatial "embedding layer" into the network and, possibly, spatially-varying network parameters. An SBNN is calibrated by matching its finite-dimensional distribution at locations on a fine gridding of space to that of a target process of interest. That process could be easy to simulate from or we have many realisations from it. We propose several variants of SBNNs, most of which are able to match the finite-dimensional distribution of the target process at the selected grid better than conventional BNNs of similar complexity. We also show that a single SBNN can be used to represent a variety of spatial processes often used in practice, such as Gaussian processes and lognormal processes. We briefly discuss the tools that could be used to make inference with SBNNs, and we conclude with a discussion of their advantages and limitations.

Neural Bayes Estimators for Irregular Spatial Data using Graph Neural Networks

Neural Bayes estimators are neural networks that approximate Bayes estimators in a fast and likelihood-free manner. They are appealing to use with spatial models and data, where estimation is often a computational bottleneck. However, neural Bayes estimators in spatial applications have, to date, been restricted to data collected over a regular grid. These estimators are also currently dependent on a prescribed set of spatial locations, which means that the neural network needs to be re-trained for new data sets; this renders them impractical in many applications and impedes their widespread adoption. In this work, we employ graph neural networks to tackle the important problem of parameter estimation from data collected over arbitrary spatial locations. In addition to extending neural Bayes estimation to irregular spatial data, our architecture leads to substantial computational benefits, since the estimator can be used with any arrangement or number of locations and independent replicates, thus amortising the cost of training for a given spatial model. We also facilitate fast uncertainty quantification by training an accompanying neural Bayes estimator that approximates a set of marginal posterior quantiles. We illustrate our methodology on Gaussian and max-stable processes. Finally, we showcase our methodology in a global sea-surface temperature application, where we estimate the parameters of a Gaussian process model in 2,161 regions, each containing thousands of irregularly-spaced data points, in just a few minutes with a single graphics processing unit.

Likelihood-free neural Bayes estimators for censored inference with peaks-over-threshold models

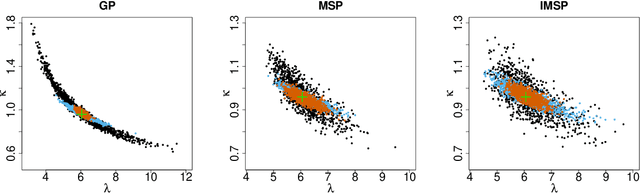
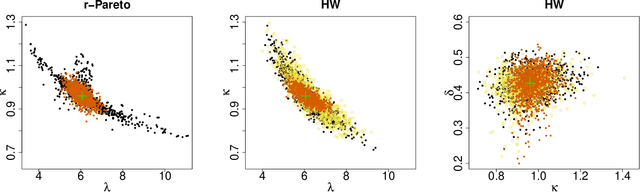
Inference for spatial extremal dependence models can be computationally burdensome in moderate-to-high dimensions due to their reliance on intractable and/or censored likelihoods. Exploiting recent advances in likelihood-free inference with neural Bayes estimators (that is, neural estimators that target Bayes estimators), we develop a novel approach to construct highly efficient estimators for censored peaks-over-threshold models by encoding censoring information in the neural network architecture. Our new method provides a paradigm shift that challenges traditional censored likelihood-based inference for spatial extremes. Our simulation studies highlight significant gains in both computational and statistical efficiency, relative to competing likelihood-based approaches, when applying our novel estimators for inference of popular extremal dependence models, such as max-stable, $r$-Pareto, and random scale mixture processes. We also illustrate that it is possible to train a single estimator for a general censoring level, obviating the need to retrain when the censoring level is changed. We illustrate the efficacy of our estimators by making fast inference on hundreds-of-thousands of high-dimensional spatial extremal dependence models to assess particulate matter 2.5 microns or less in diameter (PM2.5) concentration over the whole of Saudi Arabia.

Fast Optimal Estimation with Intractable Models using Permutation-Invariant Neural Networks

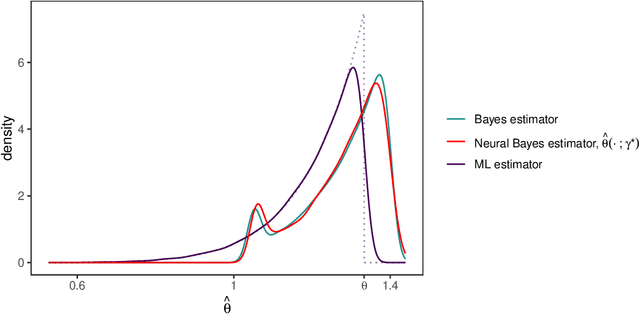
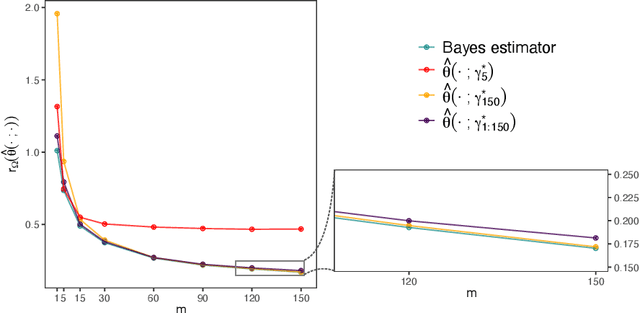
Neural networks have recently shown promise for likelihood-free inference, providing orders-of-magnitude speed-ups over classical methods. However, current implementations are suboptimal when estimating parameters from independent replicates. In this paper, we use a decision-theoretic framework to argue that permutation-invariant neural networks are ideally placed for constructing Bayes estimators for arbitrary models, provided that simulation from these models is straightforward. We illustrate the potential of these estimators on both conventional spatial models, as well as highly parameterised spatial-extremes models, and show that they considerably outperform neural estimators that do not account for replication appropriately in their network design. At the same time, they are highly competitive and much faster than traditional likelihood-based estimators. We apply our estimator on a spatial analysis of sea-surface temperature in the Red Sea where, after training, we obtain parameter estimates, and uncertainty quantification of the estimates via bootstrap sampling, from hundreds of spatial fields in a fraction of a second.

Statistical Deep Learning for Spatial and Spatio-Temporal Data

Deep neural network models have become ubiquitous in recent years, and have been applied to nearly all areas of science, engineering, and industry. These models are particularly useful for data that have strong dependencies in space (e.g., images) and time (e.g., sequences). Indeed, deep models have also been extensively used by the statistical community to model spatial and spatio-temporal data through, for example, the use of multi-level Bayesian hierarchical models and deep Gaussian processes. In this review, we first present an overview of traditional statistical and machine learning perspectives for modeling spatial and spatio-temporal data, and then focus on a variety of hybrid models that have recently been developed for latent process, data, and parameter specifications. These hybrid models integrate statistical modeling ideas with deep neural network models in order to take advantage of the strengths of each modeling paradigm. We conclude by giving an overview of computational technologies that have proven useful for these hybrid models, and with a brief discussion on future research directions.