Jordan Richards
Modeling Nonstationary Extremal Dependence via Deep Spatial Deformations
May 18, 2025Abstract:Modeling nonstationarity that often prevails in extremal dependence of spatial data can be challenging, and typically requires bespoke or complex spatial models that are difficult to estimate. Inference for stationary and isotropic models is considerably easier, but the assumptions that underpin these models are rarely met by data observed over large or topographically complex domains. A possible approach for accommodating nonstationarity in a spatial model is to warp the spatial domain to a latent space where stationarity and isotropy can be reasonably assumed. Although this approach is very flexible, estimating the warping function can be computationally expensive, and the transformation is not always guaranteed to be bijective, which may lead to physically unrealistic transformations when the domain folds onto itself. We overcome these challenges by developing deep compositional spatial models to capture nonstationarity in extremal dependence. Specifically, we focus on modeling high threshold exceedances of process functionals by leveraging efficient inference methods for limiting $r$-Pareto processes. A detailed high-dimensional simulation study demonstrates the superior performance of our model in estimating the warped space. We illustrate our method by modeling UK precipitation extremes and show that we can efficiently estimate the extremal dependence structure of data observed at thousands of locations.
Deep learning joint extremes of metocean variables using the SPAR model
Dec 20, 2024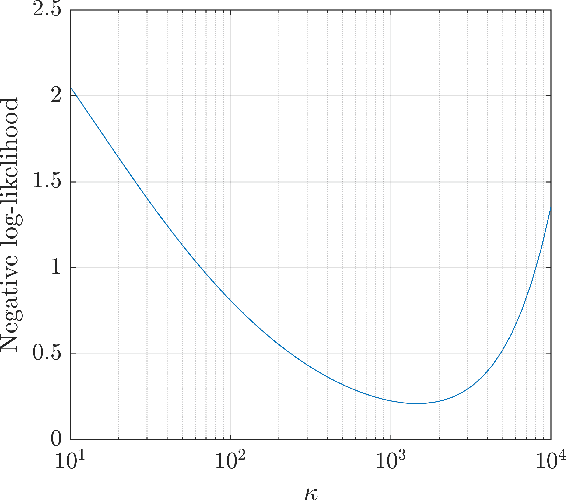
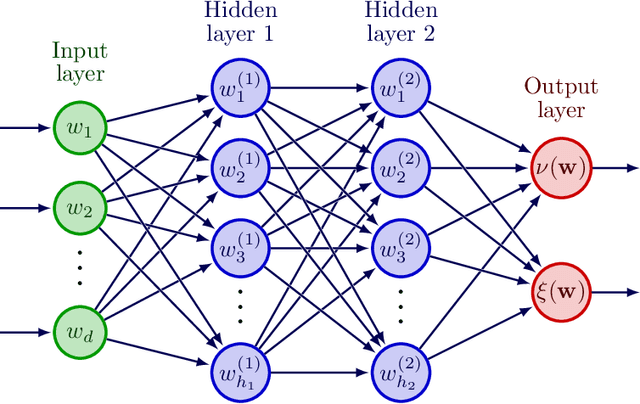
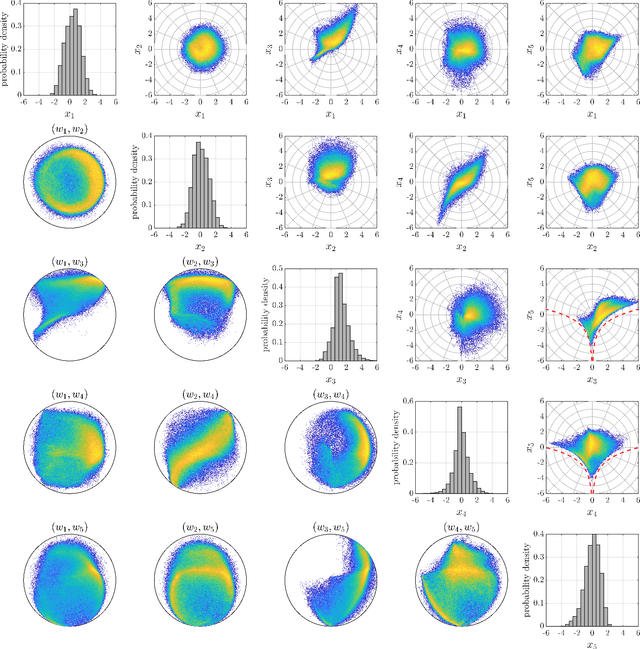
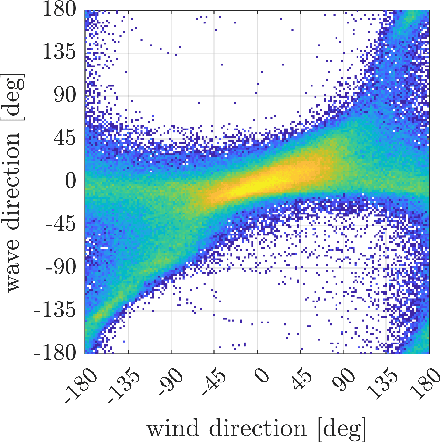
Abstract:This paper presents a novel deep learning framework for estimating multivariate joint extremes of metocean variables, based on the Semi-Parametric Angular-Radial (SPAR) model. When considered in polar coordinates, the problem of modelling multivariate extremes is transformed to one of modelling an angular density, and the tail of a univariate radial variable conditioned on angle. In the SPAR approach, the tail of the radial variable is modelled using a generalised Pareto (GP) distribution, providing a natural extension of univariate extreme value theory to the multivariate setting. In this work, we show how the method can be applied in higher dimensions, using a case study for five metocean variables: wind speed, wind direction, wave height, wave period and wave direction. The angular variable is modelled empirically, while the parameters of the GP model are approximated using fully-connected deep neural networks. Our data-driven approach provides great flexibility in the dependence structures that can be represented, together with computationally efficient routines for training the model. Furthermore, the application of the method requires fewer assumptions about the underlying distribution(s) compared to existing approaches, and an asymptotically justified means for extrapolating outside the range of observations. Using various diagnostic plots, we show that the fitted models provide a good description of the joint extremes of the metocean variables considered.
Deep Learning of Multivariate Extremes via a Geometric Representation
Jun 28, 2024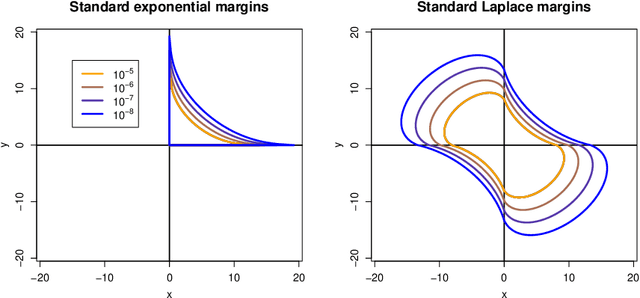
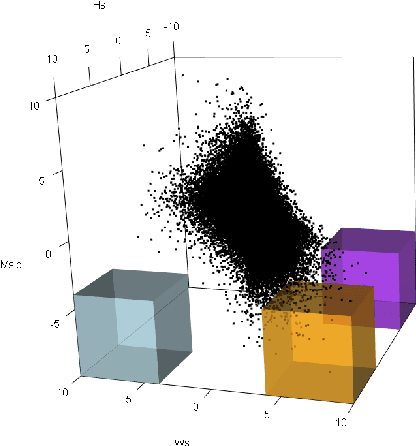
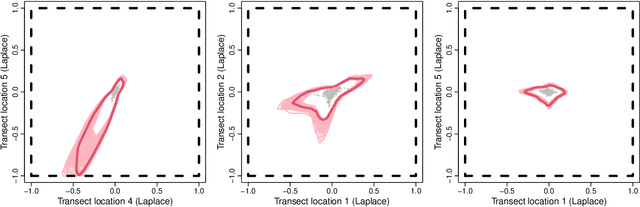
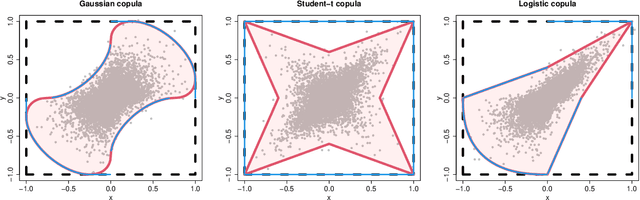
Abstract:The study of geometric extremes, where extremal dependence properties are inferred from the deterministic limiting shapes of scaled sample clouds, provides an exciting approach to modelling the extremes of multivariate data. These shapes, termed limit sets, link together several popular extremal dependence modelling frameworks. Although the geometric approach is becoming an increasingly popular modelling tool, current inference techniques are limited to a low dimensional setting (d < 4), and generally require rigid modelling assumptions. In this work, we propose a range of novel theoretical results to aid with the implementation of the geometric extremes framework and introduce the first approach to modelling limit sets using deep learning. By leveraging neural networks, we construct asymptotically-justified yet flexible semi-parametric models for extremal dependence of high-dimensional data. We showcase the efficacy of our deep approach by modelling the complex extremal dependencies between meteorological and oceanographic variables in the North Sea off the coast of the UK.
Neural Bayes Estimators for Irregular Spatial Data using Graph Neural Networks
Oct 04, 2023Abstract:Neural Bayes estimators are neural networks that approximate Bayes estimators in a fast and likelihood-free manner. They are appealing to use with spatial models and data, where estimation is often a computational bottleneck. However, neural Bayes estimators in spatial applications have, to date, been restricted to data collected over a regular grid. These estimators are also currently dependent on a prescribed set of spatial locations, which means that the neural network needs to be re-trained for new data sets; this renders them impractical in many applications and impedes their widespread adoption. In this work, we employ graph neural networks to tackle the important problem of parameter estimation from data collected over arbitrary spatial locations. In addition to extending neural Bayes estimation to irregular spatial data, our architecture leads to substantial computational benefits, since the estimator can be used with any arrangement or number of locations and independent replicates, thus amortising the cost of training for a given spatial model. We also facilitate fast uncertainty quantification by training an accompanying neural Bayes estimator that approximates a set of marginal posterior quantiles. We illustrate our methodology on Gaussian and max-stable processes. Finally, we showcase our methodology in a global sea-surface temperature application, where we estimate the parameters of a Gaussian process model in 2,161 regions, each containing thousands of irregularly-spaced data points, in just a few minutes with a single graphics processing unit.
Deep graphical regression for jointly moderate and extreme Australian wildfires
Aug 28, 2023
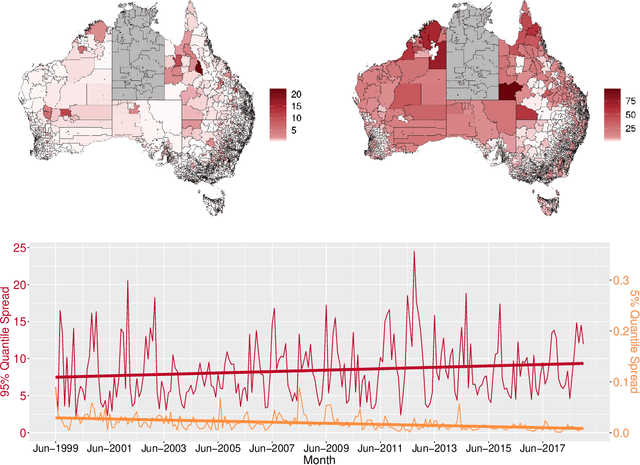

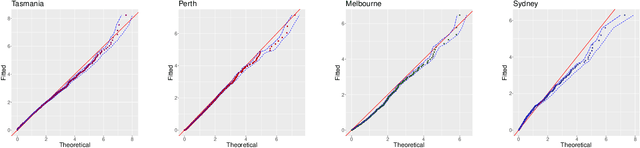
Abstract:Recent wildfires in Australia have led to considerable economic loss and property destruction, and there is increasing concern that climate change may exacerbate their intensity, duration, and frequency. hazard quantification for extreme wildfires is an important component of wildfire management, as it facilitates efficient resource distribution, adverse effect mitigation, and recovery efforts. However, although extreme wildfires are typically the most impactful, both small and moderate fires can still be devastating to local communities and ecosystems. Therefore, it is imperative to develop robust statistical methods to reliably model the full distribution of wildfire spread. We do so for a novel dataset of Australian wildfires from 1999 to 2019, and analyse monthly spread over areas approximately corresponding to Statistical Areas Level 1 and 2 (SA1/SA2) regions. Given the complex nature of wildfire ignition and spread, we exploit recent advances in statistical deep learning and extreme value theory to construct a parametric regression model using graph convolutional neural networks and the extended generalized Pareto distribution, which allows us to model wildfire spread observed on an irregular spatial domain. We highlight the efficacy of our newly proposed model and perform a wildfire hazard assessment for Australia and population-dense communities, namely Tasmania, Sydney, Melbourne, and Perth.
Likelihood-free neural Bayes estimators for censored inference with peaks-over-threshold models
Jun 29, 2023
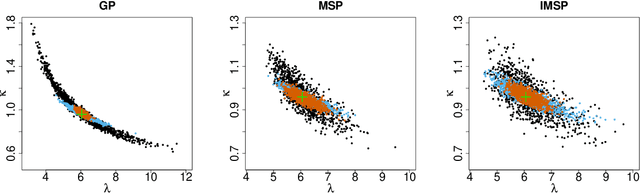

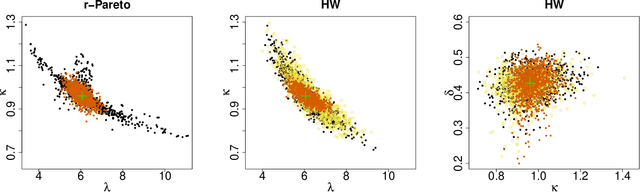
Abstract:Inference for spatial extremal dependence models can be computationally burdensome in moderate-to-high dimensions due to their reliance on intractable and/or censored likelihoods. Exploiting recent advances in likelihood-free inference with neural Bayes estimators (that is, neural estimators that target Bayes estimators), we develop a novel approach to construct highly efficient estimators for censored peaks-over-threshold models by encoding censoring information in the neural network architecture. Our new method provides a paradigm shift that challenges traditional censored likelihood-based inference for spatial extremes. Our simulation studies highlight significant gains in both computational and statistical efficiency, relative to competing likelihood-based approaches, when applying our novel estimators for inference of popular extremal dependence models, such as max-stable, $r$-Pareto, and random scale mixture processes. We also illustrate that it is possible to train a single estimator for a general censoring level, obviating the need to retrain when the censoring level is changed. We illustrate the efficacy of our estimators by making fast inference on hundreds-of-thousands of high-dimensional spatial extremal dependence models to assess particulate matter 2.5 microns or less in diameter (PM2.5) concentration over the whole of Saudi Arabia.
Insights into the drivers and spatio-temporal trends of extreme Mediterranean wildfires with statistical deep-learning
Dec 06, 2022



Abstract:Extreme wildfires continue to be a significant cause of human death and biodiversity destruction within countries that encompass the Mediterranean Basin. Recent worrying trends in wildfire activity (i.e., occurrence and spread) suggest that wildfires are likely to be highly impacted by climate change. In order to facilitate appropriate risk mitigation, it is imperative to identify the main drivers of extreme wildfires and assess their spatio-temporal trends, with a view to understanding the impacts of global warming on fire activity. To this end, we analyse the monthly burnt area due to wildfires over a region encompassing most of Europe and the Mediterranean Basin from 2001 to 2020, and identify high fire activity during this period in eastern Europe, Algeria, Italy and Portugal. We build an extreme quantile regression model with a high-dimensional predictor set describing meteorological conditions, land cover usage, and orography, for the domain. To model the complex relationships between the predictor variables and wildfires, we make use of a hybrid statistical deep-learning framework that allows us to disentangle the effects of vapour-pressure deficit (VPD), air temperature, and drought on wildfire activity. Our results highlight that whilst VPD, air temperature, and drought significantly affect wildfire occurrence, only VPD affects extreme wildfire spread. Furthermore, to gain insights into the effect of climate change on wildfire activity in the near future, we perturb VPD and temperature according to their observed trends and find evidence that global warming may lead to spatially non-uniform changes in wildfire activity.
A unifying partially-interpretable framework for neural network-based extreme quantile regression
Aug 17, 2022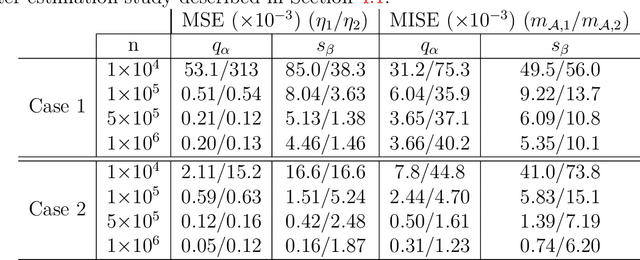
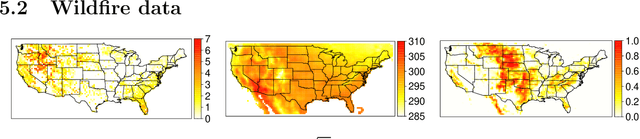
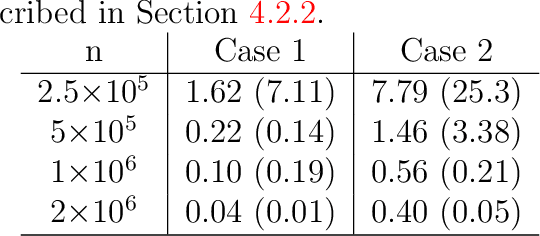
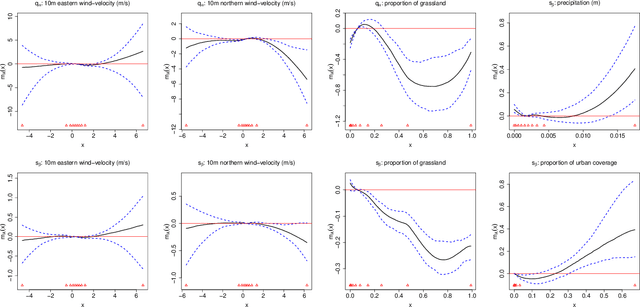
Abstract:Risk management in many environmental settings requires an understanding of the mechanisms that drive extreme events. Useful metrics for quantifying such risk are extreme quantiles of response variables conditioned on predictor variables that describe e.g., climate, biosphere and environmental states. Typically these quantiles lie outside the range of observable data and so, for estimation, require specification of parametric extreme value models within a regression framework. Classical approaches in this context utilise linear or additive relationships between predictor and response variables and suffer in either their predictive capabilities or computational efficiency; moreover, their simplicity is unlikely to capture the truly complex structures that lead to the creation of extreme wildfires. In this paper, we propose a new methodological framework for performing extreme quantile regression using artificial neutral networks, which are able to capture complex non-linear relationships and scale well to high-dimensional data. The "black box" nature of neural networks means that they lack the desirable trait of interpretability often favoured by practitioners; thus, we combine aspects of linear, and additive, models with deep learning to create partially interpretable neural networks that can be used for statistical inference but retain high prediction accuracy. To complement this methodology, we further propose a novel point process model for extreme values which overcomes the finite lower-endpoint problem associated with the generalised extreme value class of distributions. Efficacy of our unified framework is illustrated on U.S. wildfire data with a high-dimensional predictor set and we illustrate vast improvements in predictive performance over linear and spline-based regression techniques.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge