Deep learning joint extremes of metocean variables using the SPAR model
Paper and Code
Dec 20, 2024
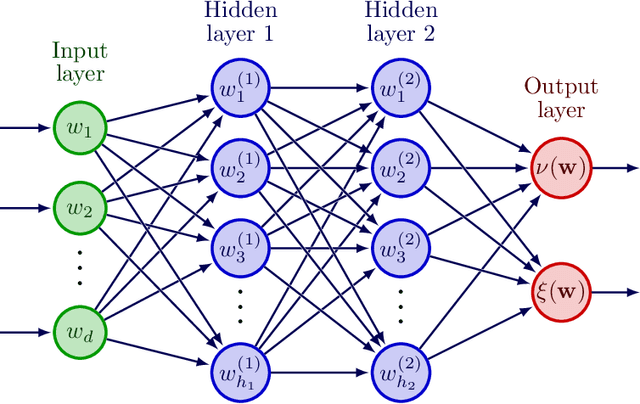
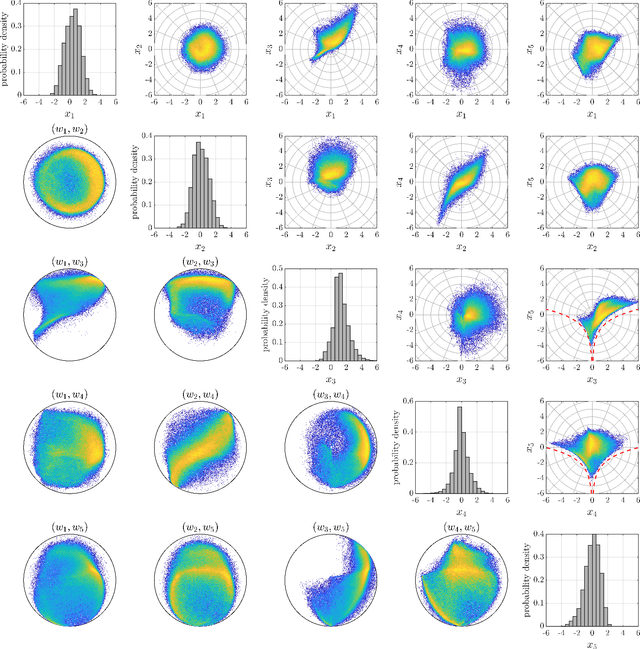
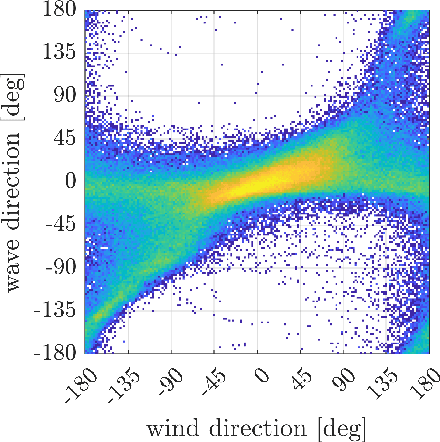
This paper presents a novel deep learning framework for estimating multivariate joint extremes of metocean variables, based on the Semi-Parametric Angular-Radial (SPAR) model. When considered in polar coordinates, the problem of modelling multivariate extremes is transformed to one of modelling an angular density, and the tail of a univariate radial variable conditioned on angle. In the SPAR approach, the tail of the radial variable is modelled using a generalised Pareto (GP) distribution, providing a natural extension of univariate extreme value theory to the multivariate setting. In this work, we show how the method can be applied in higher dimensions, using a case study for five metocean variables: wind speed, wind direction, wave height, wave period and wave direction. The angular variable is modelled empirically, while the parameters of the GP model are approximated using fully-connected deep neural networks. Our data-driven approach provides great flexibility in the dependence structures that can be represented, together with computationally efficient routines for training the model. Furthermore, the application of the method requires fewer assumptions about the underlying distribution(s) compared to existing approaches, and an asymptotically justified means for extrapolating outside the range of observations. Using various diagnostic plots, we show that the fitted models provide a good description of the joint extremes of the metocean variables considered.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge