A unifying partially-interpretable framework for neural network-based extreme quantile regression
Paper and Code
Aug 17, 2022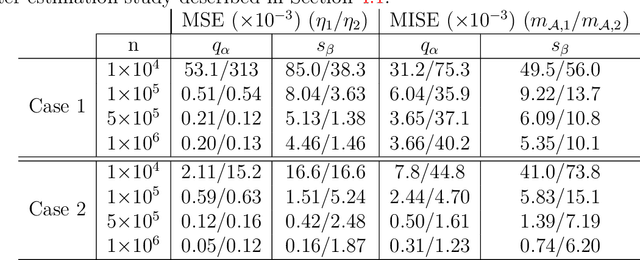
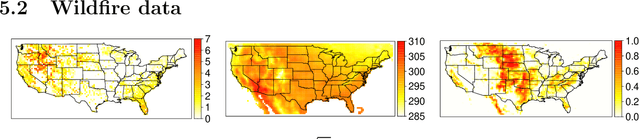
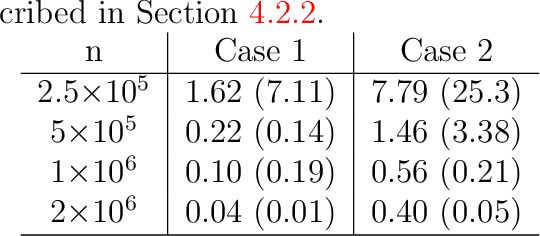
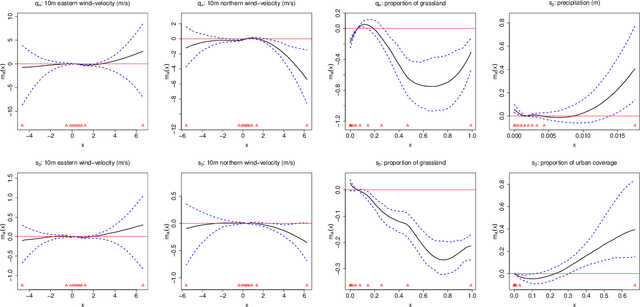
Risk management in many environmental settings requires an understanding of the mechanisms that drive extreme events. Useful metrics for quantifying such risk are extreme quantiles of response variables conditioned on predictor variables that describe e.g., climate, biosphere and environmental states. Typically these quantiles lie outside the range of observable data and so, for estimation, require specification of parametric extreme value models within a regression framework. Classical approaches in this context utilise linear or additive relationships between predictor and response variables and suffer in either their predictive capabilities or computational efficiency; moreover, their simplicity is unlikely to capture the truly complex structures that lead to the creation of extreme wildfires. In this paper, we propose a new methodological framework for performing extreme quantile regression using artificial neutral networks, which are able to capture complex non-linear relationships and scale well to high-dimensional data. The "black box" nature of neural networks means that they lack the desirable trait of interpretability often favoured by practitioners; thus, we combine aspects of linear, and additive, models with deep learning to create partially interpretable neural networks that can be used for statistical inference but retain high prediction accuracy. To complement this methodology, we further propose a novel point process model for extreme values which overcomes the finite lower-endpoint problem associated with the generalised extreme value class of distributions. Efficacy of our unified framework is illustrated on U.S. wildfire data with a high-dimensional predictor set and we illustrate vast improvements in predictive performance over linear and spline-based regression techniques.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge