Neural Methods for Amortised Parameter Inference

Simulation-based methods for making statistical inference have evolved dramatically over the past 50 years, keeping pace with technological advancements. The field is undergoing a new revolution as it embraces the representational capacity of neural networks, optimisation libraries, and graphics processing units for learning complex mappings between data and inferential targets. The resulting tools are amortised, in the sense that they allow inference to be made quickly through fast feedforward operations. In this article we review recent progress made in the context of point estimation, approximate Bayesian inference, the automatic construction of summary statistics, and likelihood approximation. The review also covers available software, and includes a simple illustration to showcase the wide array of tools available for amortised inference and the benefits they offer over state-of-the-art Markov chain Monte Carlo methods. The article concludes with an overview of relevant topics and an outlook on future research directions.

At the junction between deep learning and statistics of extremes: formalizing the landslide hazard definition

The most adopted definition of landslide hazard combines spatial information about landslide location (susceptibility), threat (intensity), and frequency (return period). Only the first two elements are usually considered and estimated when working over vast areas. Even then, separate models constitute the standard, with frequency being rarely investigated. Frequency and intensity are intertwined and depend on each other because larger events occur less frequently and vice versa. However, due to the lack of multi-temporal inventories and joint statistical models, modelling such properties via a unified hazard model has always been challenging and has yet to be attempted. Here, we develop a unified model to estimate landslide hazard at the slope unit level to address such gaps. We employed deep learning, combined with a model motivated by extreme-value theory to analyse an inventory of 30 years of observed rainfall-triggered landslides in Nepal and assess landslide hazard for multiple return periods. We also use our model to further explore landslide hazard for the same return periods under different climate change scenarios up to the end of the century. Our results show that the proposed model performs excellently and can be used to model landslide hazard in a unified manner. Geomorphologically, we find that under both climate change scenarios (SSP245 and SSP885), landslide hazard is likely to increase up to two times on average in the lower Himalayan regions while remaining the same in the middle Himalayan region whilst decreasing slightly in the upper Himalayan region areas.

Neural Bayes Estimators for Irregular Spatial Data using Graph Neural Networks

Neural Bayes estimators are neural networks that approximate Bayes estimators in a fast and likelihood-free manner. They are appealing to use with spatial models and data, where estimation is often a computational bottleneck. However, neural Bayes estimators in spatial applications have, to date, been restricted to data collected over a regular grid. These estimators are also currently dependent on a prescribed set of spatial locations, which means that the neural network needs to be re-trained for new data sets; this renders them impractical in many applications and impedes their widespread adoption. In this work, we employ graph neural networks to tackle the important problem of parameter estimation from data collected over arbitrary spatial locations. In addition to extending neural Bayes estimation to irregular spatial data, our architecture leads to substantial computational benefits, since the estimator can be used with any arrangement or number of locations and independent replicates, thus amortising the cost of training for a given spatial model. We also facilitate fast uncertainty quantification by training an accompanying neural Bayes estimator that approximates a set of marginal posterior quantiles. We illustrate our methodology on Gaussian and max-stable processes. Finally, we showcase our methodology in a global sea-surface temperature application, where we estimate the parameters of a Gaussian process model in 2,161 regions, each containing thousands of irregularly-spaced data points, in just a few minutes with a single graphics processing unit.

Deep graphical regression for jointly moderate and extreme Australian wildfires

Recent wildfires in Australia have led to considerable economic loss and property destruction, and there is increasing concern that climate change may exacerbate their intensity, duration, and frequency. hazard quantification for extreme wildfires is an important component of wildfire management, as it facilitates efficient resource distribution, adverse effect mitigation, and recovery efforts. However, although extreme wildfires are typically the most impactful, both small and moderate fires can still be devastating to local communities and ecosystems. Therefore, it is imperative to develop robust statistical methods to reliably model the full distribution of wildfire spread. We do so for a novel dataset of Australian wildfires from 1999 to 2019, and analyse monthly spread over areas approximately corresponding to Statistical Areas Level 1 and 2 (SA1/SA2) regions. Given the complex nature of wildfire ignition and spread, we exploit recent advances in statistical deep learning and extreme value theory to construct a parametric regression model using graph convolutional neural networks and the extended generalized Pareto distribution, which allows us to model wildfire spread observed on an irregular spatial domain. We highlight the efficacy of our newly proposed model and perform a wildfire hazard assessment for Australia and population-dense communities, namely Tasmania, Sydney, Melbourne, and Perth.

Flexible and efficient spatial extremes emulation via variational autoencoders

Many real-world processes have complex tail dependence structures that cannot be characterized using classical Gaussian processes. More flexible spatial extremes models such as Gaussian scale mixtures and single-station conditioning models exhibit appealing extremal dependence properties but are often exceedingly prohibitive to fit and simulate from. In this paper, we develop a new spatial extremes model that has flexible and non-stationary dependence properties, and we integrate it in the encoding-decoding structure of a variational autoencoder (extVAE). The extVAE can be used as a spatio-temporal emulator that characterizes the distribution of potential mechanistic model output states and produces outputs that have the same properties as the inputs, especially in the tail. Through extensive simulation studies, we show that our extVAE is vastly more time-efficient than traditional Bayesian inference while also outperforming many spatial extremes models with a stationary dependence structure. To further demonstrate the computational power of the extVAE, we analyze a high-resolution satellite-derived dataset of sea surface temperature in the Red Sea, which includes daily measurements at 16703 grid cells.

Likelihood-free neural Bayes estimators for censored inference with peaks-over-threshold models

Inference for spatial extremal dependence models can be computationally burdensome in moderate-to-high dimensions due to their reliance on intractable and/or censored likelihoods. Exploiting recent advances in likelihood-free inference with neural Bayes estimators (that is, neural estimators that target Bayes estimators), we develop a novel approach to construct highly efficient estimators for censored peaks-over-threshold models by encoding censoring information in the neural network architecture. Our new method provides a paradigm shift that challenges traditional censored likelihood-based inference for spatial extremes. Our simulation studies highlight significant gains in both computational and statistical efficiency, relative to competing likelihood-based approaches, when applying our novel estimators for inference of popular extremal dependence models, such as max-stable, $r$-Pareto, and random scale mixture processes. We also illustrate that it is possible to train a single estimator for a general censoring level, obviating the need to retrain when the censoring level is changed. We illustrate the efficacy of our estimators by making fast inference on hundreds-of-thousands of high-dimensional spatial extremal dependence models to assess particulate matter 2.5 microns or less in diameter (PM2.5) concentration over the whole of Saudi Arabia.

Insights into the drivers and spatio-temporal trends of extreme Mediterranean wildfires with statistical deep-learning

Extreme wildfires continue to be a significant cause of human death and biodiversity destruction within countries that encompass the Mediterranean Basin. Recent worrying trends in wildfire activity (i.e., occurrence and spread) suggest that wildfires are likely to be highly impacted by climate change. In order to facilitate appropriate risk mitigation, it is imperative to identify the main drivers of extreme wildfires and assess their spatio-temporal trends, with a view to understanding the impacts of global warming on fire activity. To this end, we analyse the monthly burnt area due to wildfires over a region encompassing most of Europe and the Mediterranean Basin from 2001 to 2020, and identify high fire activity during this period in eastern Europe, Algeria, Italy and Portugal. We build an extreme quantile regression model with a high-dimensional predictor set describing meteorological conditions, land cover usage, and orography, for the domain. To model the complex relationships between the predictor variables and wildfires, we make use of a hybrid statistical deep-learning framework that allows us to disentangle the effects of vapour-pressure deficit (VPD), air temperature, and drought on wildfire activity. Our results highlight that whilst VPD, air temperature, and drought significantly affect wildfire occurrence, only VPD affects extreme wildfire spread. Furthermore, to gain insights into the effect of climate change on wildfire activity in the near future, we perturb VPD and temperature according to their observed trends and find evidence that global warming may lead to spatially non-uniform changes in wildfire activity.

Fast Optimal Estimation with Intractable Models using Permutation-Invariant Neural Networks

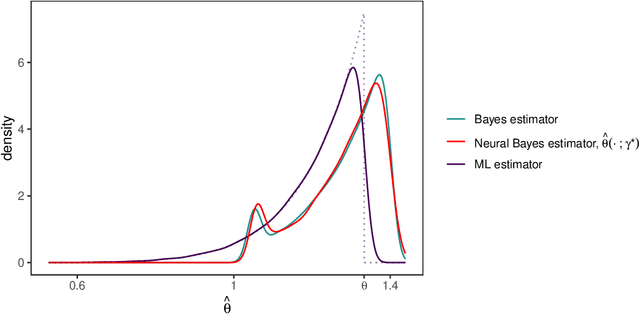
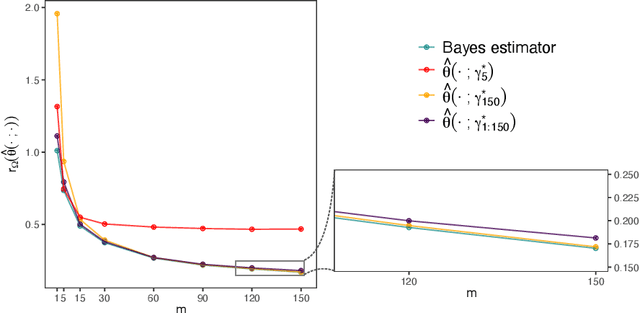
Neural networks have recently shown promise for likelihood-free inference, providing orders-of-magnitude speed-ups over classical methods. However, current implementations are suboptimal when estimating parameters from independent replicates. In this paper, we use a decision-theoretic framework to argue that permutation-invariant neural networks are ideally placed for constructing Bayes estimators for arbitrary models, provided that simulation from these models is straightforward. We illustrate the potential of these estimators on both conventional spatial models, as well as highly parameterised spatial-extremes models, and show that they considerably outperform neural estimators that do not account for replication appropriately in their network design. At the same time, they are highly competitive and much faster than traditional likelihood-based estimators. We apply our estimator on a spatial analysis of sea-surface temperature in the Red Sea where, after training, we obtain parameter estimates, and uncertainty quantification of the estimates via bootstrap sampling, from hundreds of spatial fields in a fraction of a second.

A unifying partially-interpretable framework for neural network-based extreme quantile regression

Risk management in many environmental settings requires an understanding of the mechanisms that drive extreme events. Useful metrics for quantifying such risk are extreme quantiles of response variables conditioned on predictor variables that describe e.g., climate, biosphere and environmental states. Typically these quantiles lie outside the range of observable data and so, for estimation, require specification of parametric extreme value models within a regression framework. Classical approaches in this context utilise linear or additive relationships between predictor and response variables and suffer in either their predictive capabilities or computational efficiency; moreover, their simplicity is unlikely to capture the truly complex structures that lead to the creation of extreme wildfires. In this paper, we propose a new methodological framework for performing extreme quantile regression using artificial neutral networks, which are able to capture complex non-linear relationships and scale well to high-dimensional data. The "black box" nature of neural networks means that they lack the desirable trait of interpretability often favoured by practitioners; thus, we combine aspects of linear, and additive, models with deep learning to create partially interpretable neural networks that can be used for statistical inference but retain high prediction accuracy. To complement this methodology, we further propose a novel point process model for extreme values which overcomes the finite lower-endpoint problem associated with the generalised extreme value class of distributions. Efficacy of our unified framework is illustrated on U.S. wildfire data with a high-dimensional predictor set and we illustrate vast improvements in predictive performance over linear and spline-based regression techniques.