Echo State Networks for Spatio-Temporal Area-Level Data

Spatio-temporal area-level datasets play a critical role in official statistics, providing valuable insights for policy-making and regional planning. Accurate modeling and forecasting of these datasets can be extremely useful for policymakers to develop informed strategies for future planning. Echo State Networks (ESNs) are efficient methods for capturing nonlinear temporal dynamics and generating forecasts. However, ESNs lack a direct mechanism to account for the neighborhood structure inherent in area-level data. Ignoring these spatial relationships can significantly compromise the accuracy and utility of forecasts. In this paper, we incorporate approximate graph spectral filters at the input stage of the ESN, thereby improving forecast accuracy while preserving the model's computational efficiency during training. We demonstrate the effectiveness of our approach using Eurostat's tourism occupancy dataset and show how it can support more informed decision-making in policy and planning contexts.

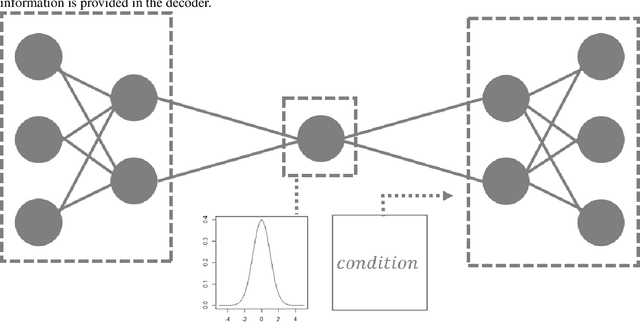
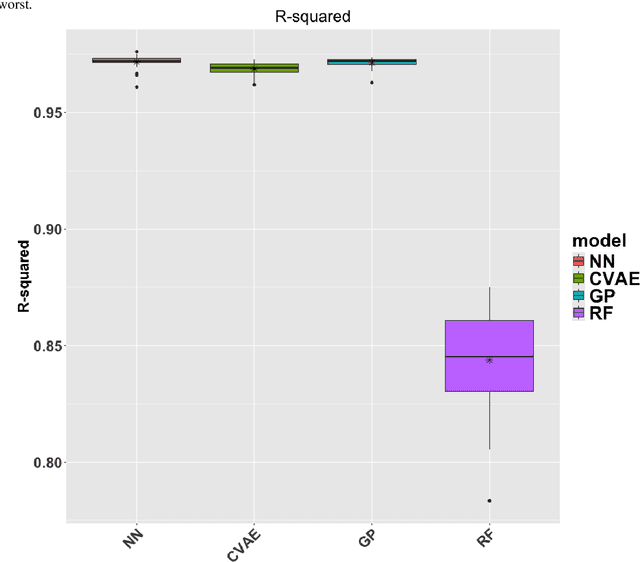
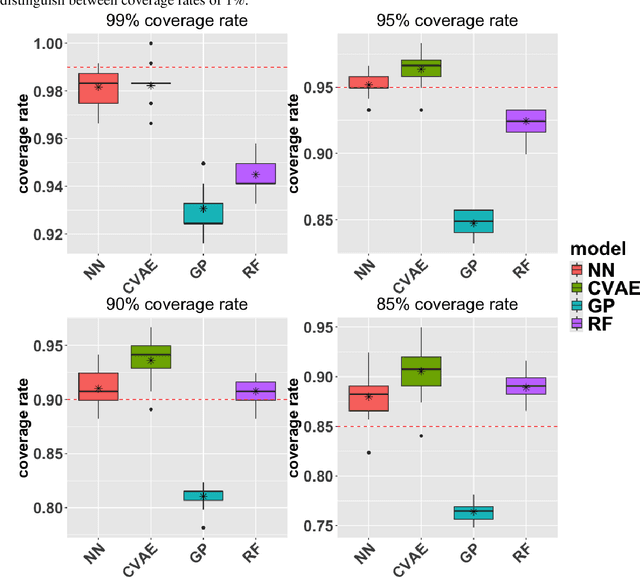
Uncertainty-enabled machine learning for emulation of regional sea-level change caused by the Antarctic Ice Sheet

Projecting sea-level change in various climate-change scenarios typically involves running forward simulations of the Earth's gravitational, rotational and deformational (GRD) response to ice mass change, which requires high computational cost and time. Here we build neural-network emulators of sea-level change at 27 coastal locations, due to the GRD effects associated with future Antarctic Ice Sheet mass change over the 21st century. The emulators are based on datasets produced using a numerical solver for the static sea-level equation and published ISMIP6-2100 ice-sheet model simulations referenced in the IPCC AR6 report. We show that the neural-network emulators have an accuracy that is competitive with baseline machine learning emulators. In order to quantify uncertainty, we derive well-calibrated prediction intervals for simulated sea-level change via a linear regression postprocessing technique that uses (nonlinear) machine learning model outputs, a technique that has previously been applied to numerical climate models. We also demonstrate substantial gains in computational efficiency: a feedforward neural-network emulator exhibits on the order of 100 times speedup in comparison to the numerical sea-level equation solver that is used for training.

Flexible and efficient spatial extremes emulation via variational autoencoders

Many real-world processes have complex tail dependence structures that cannot be characterized using classical Gaussian processes. More flexible spatial extremes models such as Gaussian scale mixtures and single-station conditioning models exhibit appealing extremal dependence properties but are often exceedingly prohibitive to fit and simulate from. In this paper, we develop a new spatial extremes model that has flexible and non-stationary dependence properties, and we integrate it in the encoding-decoding structure of a variational autoencoder (extVAE). The extVAE can be used as a spatio-temporal emulator that characterizes the distribution of potential mechanistic model output states and produces outputs that have the same properties as the inputs, especially in the tail. Through extensive simulation studies, we show that our extVAE is vastly more time-efficient than traditional Bayesian inference while also outperforming many spatial extremes models with a stationary dependence structure. To further demonstrate the computational power of the extVAE, we analyze a high-resolution satellite-derived dataset of sea surface temperature in the Red Sea, which includes daily measurements at 16703 grid cells.

Statistical Deep Learning for Spatial and Spatio-Temporal Data

Deep neural network models have become ubiquitous in recent years, and have been applied to nearly all areas of science, engineering, and industry. These models are particularly useful for data that have strong dependencies in space (e.g., images) and time (e.g., sequences). Indeed, deep models have also been extensively used by the statistical community to model spatial and spatio-temporal data through, for example, the use of multi-level Bayesian hierarchical models and deep Gaussian processes. In this review, we first present an overview of traditional statistical and machine learning perspectives for modeling spatial and spatio-temporal data, and then focus on a variety of hybrid models that have recently been developed for latent process, data, and parameter specifications. These hybrid models integrate statistical modeling ideas with deep neural network models in order to take advantage of the strengths of each modeling paradigm. We conclude by giving an overview of computational technologies that have proven useful for these hybrid models, and with a brief discussion on future research directions.

Bayesian Inverse Reinforcement Learning for Collective Animal Movement

Agent-based methods allow for defining simple rules that generate complex group behaviors. The governing rules of such models are typically set a priori and parameters are tuned from observed behavior trajectories. Instead of making simplifying assumptions across all anticipated scenarios, inverse reinforcement learning provides inference on the short-term (local) rules governing long term behavior policies by using properties of a Markov decision process. We use the computationally efficient linearly-solvable Markov decision process to learn the local rules governing collective movement for a simulation of the self propelled-particle (SPP) model and a data application for a captive guppy population. The estimation of the behavioral decision costs is done in a Bayesian framework with basis function smoothing. We recover the true costs in the SPP simulation and find the guppies value collective movement more than targeted movement toward shelter.

Deep Integro-Difference Equation Models for Spatio-Temporal Forecasting

Integro-difference equation (IDE) models describe the conditional dependence between the spatial process at a future time point and the process at the present time point through an integral operator. Nonlinearity or temporal dependence in the dynamics is often captured by allowing the operator parameters to vary temporally, or by re-fitting a model with a temporally-invariant linear operator at each time point in a sliding window. Both procedures tend to be excellent for prediction purposes over small time horizons, but are generally time-consuming and, crucially, do not provide a global prior model for the temporally-varying dynamics that is realistic. Here, we tackle these two issues by using a deep convolution neural network (CNN) in a hierarchical statistical IDE framework, where the CNN is designed to extract process dynamics from the process' most recent behaviour. Once the CNN is fitted, probabilistic forecasting can be done extremely quickly online using an ensemble Kalman filter with no requirement for repeated parameter estimation. We conduct an experiment where we train the model using 13 years of daily sea-surface temperature data in the North Atlantic Ocean. Forecasts are seen to be accurate and calibrated. A key advantage of our approach is that the CNN provides a global prior model for the dynamics that is realistic, interpretable, and computationally efficient. We show the versatility of the approach by successfully producing 10-minute nowcasts of weather radar reflectivities in Sydney using the same model that was trained on daily sea-surface temperature data in the North Atlantic Ocean.

Comparison of Deep Neural Networks and Deep Hierarchical Models for Spatio-Temporal Data

Spatio-temporal data are ubiquitous in the agricultural, ecological, and environmental sciences, and their study is important for understanding and predicting a wide variety of processes. One of the difficulties with modeling spatial processes that change in time is the complexity of the dependence structures that must describe how such a process varies, and the presence of high-dimensional complex data sets and large prediction domains. It is particularly challenging to specify parameterizations for nonlinear dynamic spatio-temporal models (DSTMs) that are simultaneously useful scientifically and efficient computationally. Statisticians have developed deep hierarchical models that can accommodate process complexity as well as the uncertainties in the predictions and inference. However, these models can be expensive and are typically application specific. On the other hand, the machine learning community has developed alternative "deep learning" approaches for nonlinear spatio-temporal modeling. These models are flexible yet are typically not implemented in a probabilistic framework. The two paradigms have many things in common and suggest hybrid approaches that can benefit from elements of each framework. This overview paper presents a brief introduction to the deep hierarchical DSTM (DH-DSTM) framework, and deep models in machine learning, culminating with the deep neural DSTM (DN-DSTM). Recent approaches that combine elements from DH-DSTMs and echo state network DN-DSTMs are presented as illustrations.

Deep Echo State Networks with Uncertainty Quantification for Spatio-Temporal Forecasting

Long-lead forecasting for spatio-temporal systems can often entail complex nonlinear dynamics that are difficult to specify it a priori. Current statistical methodologies for modeling these processes are often highly parameterized and thus, challenging to implement from a computational perspective. One potential parsimonious solution to this problem is a method from the dynamical systems and engineering literature referred to as an echo state network (ESN). ESN models use so-called {\it reservoir computing} to efficiently compute recurrent neural network (RNN) forecasts. Moreover, so-called "deep" models have recently been shown to be successful at predicting high-dimensional complex nonlinear processes, particularly those with multiple spatial and temporal scales of variability (such as we often find in spatio-temporal environmental data). Here we introduce a deep ensemble ESN (D-EESN) model. We present two versions of this model for spatio-temporal processes that both produce forecasts and associated measures of uncertainty. The first approach utilizes a bootstrap ensemble framework and the second is developed within a hierarchical Bayesian framework (BD-EESN). This more general hierarchical Bayesian framework naturally accommodates non-Gaussian data types and multiple levels of uncertainties. The methodology is first applied to a data set simulated from a novel non-Gaussian multiscale Lorenz-96 dynamical system simulation model and then to a long-lead United States (U.S.) soil moisture forecasting application.

Bayesian Recurrent Neural Network Models for Forecasting and Quantifying Uncertainty in Spatial-Temporal Data

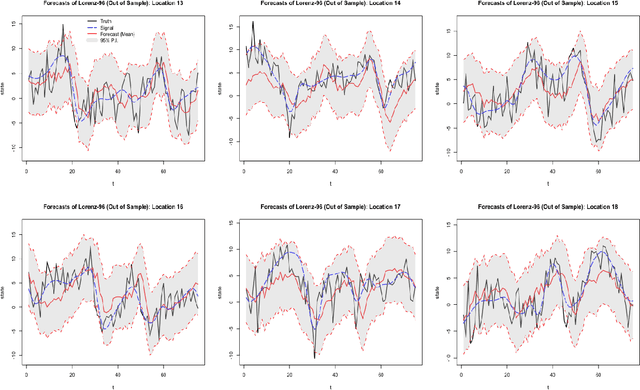
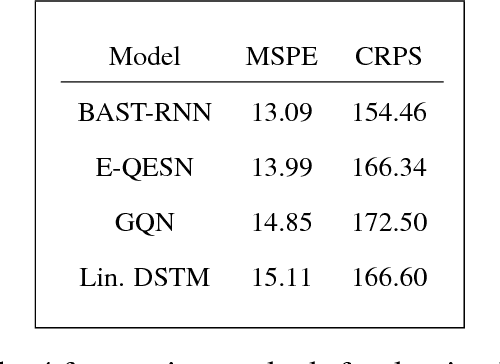
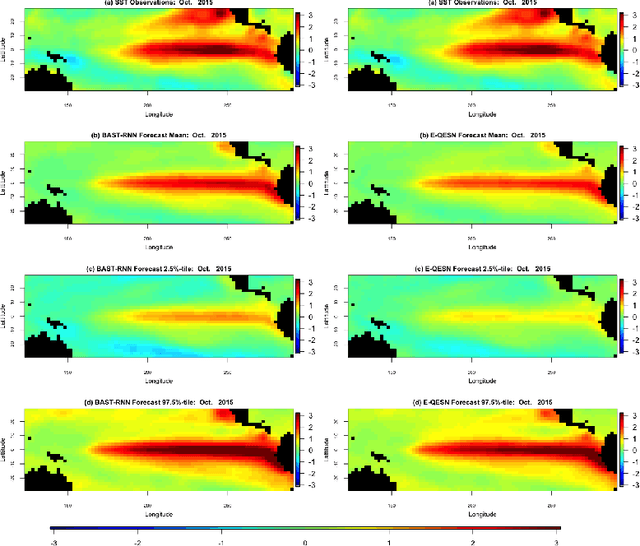
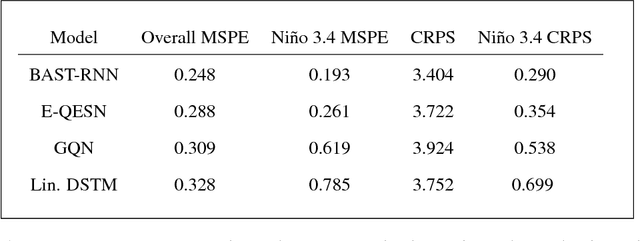
Recurrent neural networks (RNNs) are nonlinear dynamical models commonly used in the machine learning and dynamical systems literature to represent complex dynamical or sequential relationships between variables. More recently, as deep learning models have become more common, RNNs have been used to forecast increasingly complicated systems. Dynamical spatio-temporal processes represent a class of complex systems that can potentially benefit from these types of models. Although the RNN literature is expansive and highly developed, uncertainty quantification is often ignored. Even when considered, the uncertainty is generally quantified without the use of a rigorous framework, such as a fully Bayesian setting. Here we attempt to quantify uncertainty in a more formal framework while maintaining the forecast accuracy that makes these models appealing, by presenting a Bayesian RNN model for nonlinear spatio-temporal forecasting. Additionally, we make simple modifications to the basic RNN to help accommodate the unique nature of nonlinear spatio-temporal data. The proposed model is applied to a Lorenz simulation and two real-world nonlinear spatio-temporal forecasting applications.

An Ensemble Quadratic Echo State Network for Nonlinear Spatio-Temporal Forecasting

Spatio-temporal data and processes are prevalent across a wide variety of scientific disciplines. These processes are often characterized by nonlinear time dynamics that include interactions across multiple scales of spatial and temporal variability. The data sets associated with many of these processes are increasing in size due to advances in automated data measurement, management, and numerical simulator output. Non- linear spatio-temporal models have only recently seen interest in statistics, but there are many classes of such models in the engineering and geophysical sciences. Tradi- tionally, these models are more heuristic than those that have been presented in the statistics literature, but are often intuitive and quite efficient computationally. We show here that with fairly simple, but important, enhancements, the echo state net- work (ESN) machine learning approach can be used to generate long-lead forecasts of nonlinear spatio-temporal processes, with reasonable uncertainty quantification, and at only a fraction of the computational expense of a traditional parametric nonlinear spatio-temporal models.