Deep Echo State Networks with Uncertainty Quantification for Spatio-Temporal Forecasting

Long-lead forecasting for spatio-temporal systems can often entail complex nonlinear dynamics that are difficult to specify it a priori. Current statistical methodologies for modeling these processes are often highly parameterized and thus, challenging to implement from a computational perspective. One potential parsimonious solution to this problem is a method from the dynamical systems and engineering literature referred to as an echo state network (ESN). ESN models use so-called {\it reservoir computing} to efficiently compute recurrent neural network (RNN) forecasts. Moreover, so-called "deep" models have recently been shown to be successful at predicting high-dimensional complex nonlinear processes, particularly those with multiple spatial and temporal scales of variability (such as we often find in spatio-temporal environmental data). Here we introduce a deep ensemble ESN (D-EESN) model. We present two versions of this model for spatio-temporal processes that both produce forecasts and associated measures of uncertainty. The first approach utilizes a bootstrap ensemble framework and the second is developed within a hierarchical Bayesian framework (BD-EESN). This more general hierarchical Bayesian framework naturally accommodates non-Gaussian data types and multiple levels of uncertainties. The methodology is first applied to a data set simulated from a novel non-Gaussian multiscale Lorenz-96 dynamical system simulation model and then to a long-lead United States (U.S.) soil moisture forecasting application.

Bayesian Recurrent Neural Network Models for Forecasting and Quantifying Uncertainty in Spatial-Temporal Data

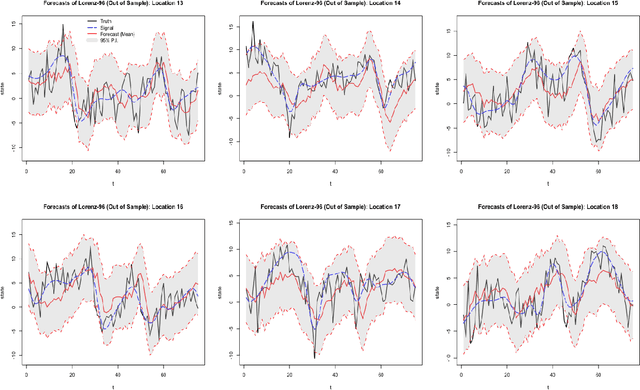
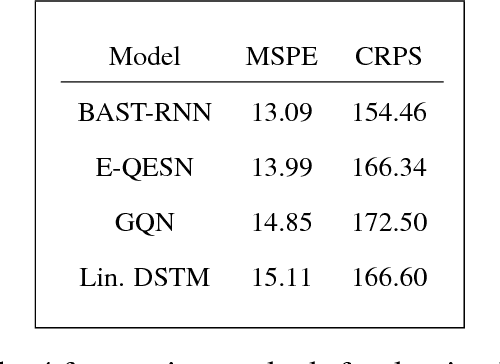
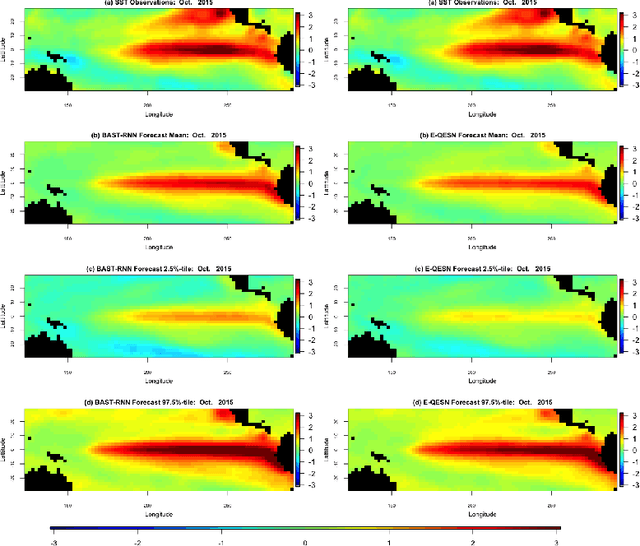
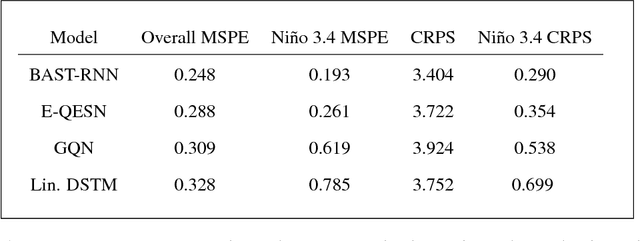
Recurrent neural networks (RNNs) are nonlinear dynamical models commonly used in the machine learning and dynamical systems literature to represent complex dynamical or sequential relationships between variables. More recently, as deep learning models have become more common, RNNs have been used to forecast increasingly complicated systems. Dynamical spatio-temporal processes represent a class of complex systems that can potentially benefit from these types of models. Although the RNN literature is expansive and highly developed, uncertainty quantification is often ignored. Even when considered, the uncertainty is generally quantified without the use of a rigorous framework, such as a fully Bayesian setting. Here we attempt to quantify uncertainty in a more formal framework while maintaining the forecast accuracy that makes these models appealing, by presenting a Bayesian RNN model for nonlinear spatio-temporal forecasting. Additionally, we make simple modifications to the basic RNN to help accommodate the unique nature of nonlinear spatio-temporal data. The proposed model is applied to a Lorenz simulation and two real-world nonlinear spatio-temporal forecasting applications.

An Ensemble Quadratic Echo State Network for Nonlinear Spatio-Temporal Forecasting

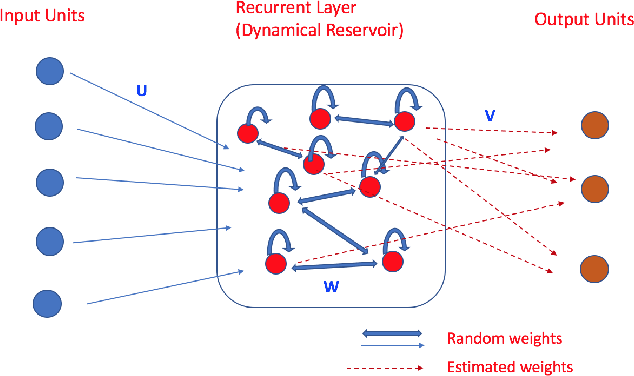
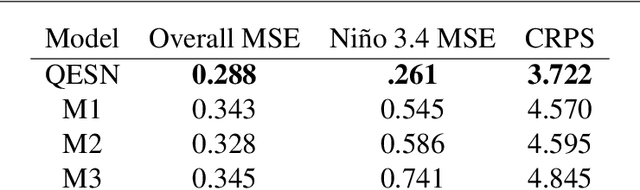
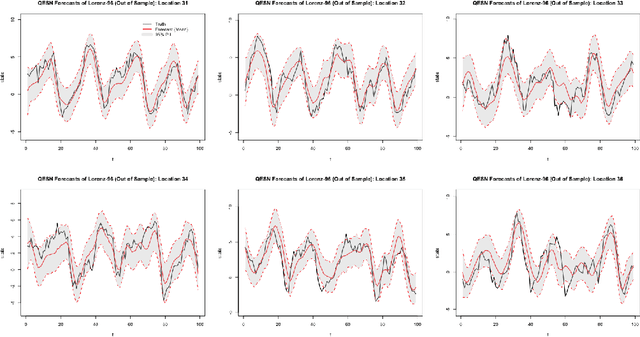
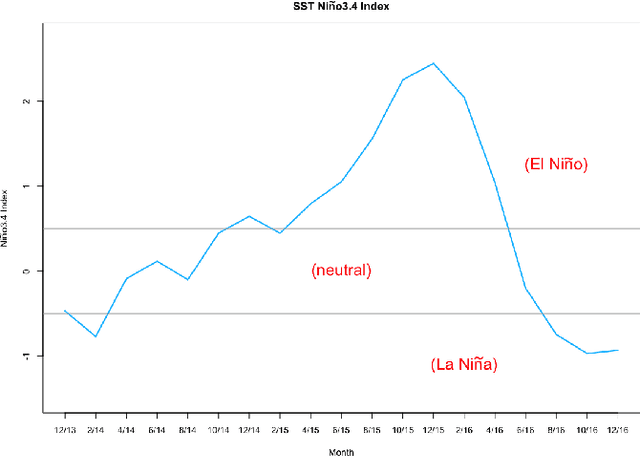
Spatio-temporal data and processes are prevalent across a wide variety of scientific disciplines. These processes are often characterized by nonlinear time dynamics that include interactions across multiple scales of spatial and temporal variability. The data sets associated with many of these processes are increasing in size due to advances in automated data measurement, management, and numerical simulator output. Non- linear spatio-temporal models have only recently seen interest in statistics, but there are many classes of such models in the engineering and geophysical sciences. Tradi- tionally, these models are more heuristic than those that have been presented in the statistics literature, but are often intuitive and quite efficient computationally. We show here that with fairly simple, but important, enhancements, the echo state net- work (ESN) machine learning approach can be used to generate long-lead forecasts of nonlinear spatio-temporal processes, with reasonable uncertainty quantification, and at only a fraction of the computational expense of a traditional parametric nonlinear spatio-temporal models.