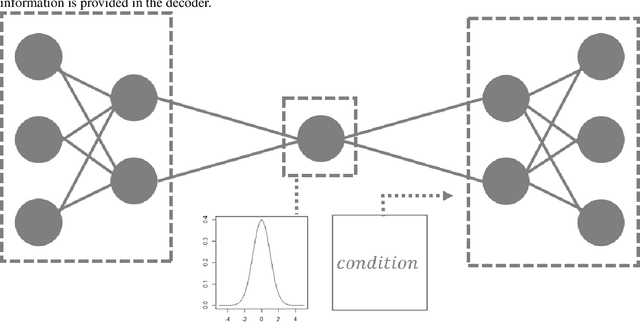
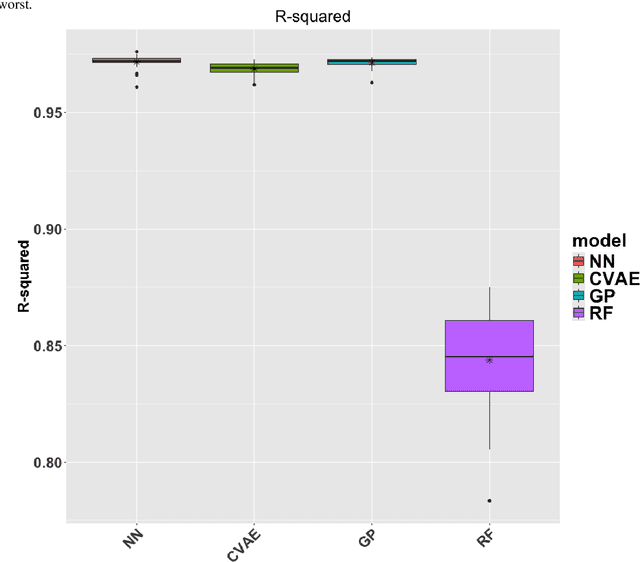
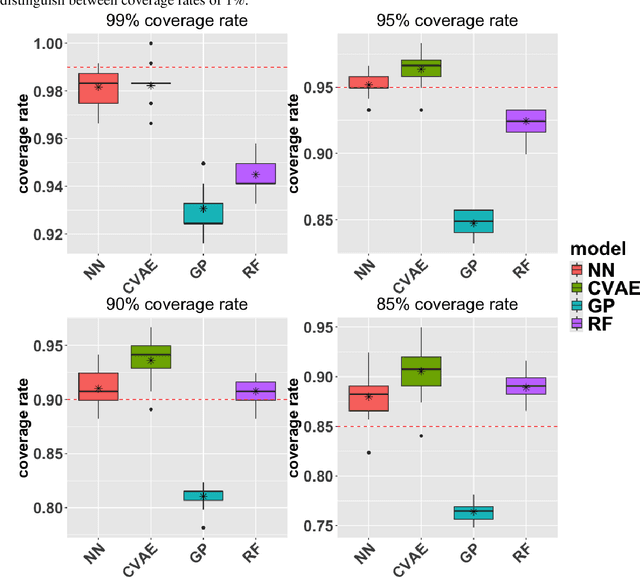
Uncertainty-enabled machine learning for emulation of regional sea-level change caused by the Antarctic Ice Sheet

Projecting sea-level change in various climate-change scenarios typically involves running forward simulations of the Earth's gravitational, rotational and deformational (GRD) response to ice mass change, which requires high computational cost and time. Here we build neural-network emulators of sea-level change at 27 coastal locations, due to the GRD effects associated with future Antarctic Ice Sheet mass change over the 21st century. The emulators are based on datasets produced using a numerical solver for the static sea-level equation and published ISMIP6-2100 ice-sheet model simulations referenced in the IPCC AR6 report. We show that the neural-network emulators have an accuracy that is competitive with baseline machine learning emulators. In order to quantify uncertainty, we derive well-calibrated prediction intervals for simulated sea-level change via a linear regression postprocessing technique that uses (nonlinear) machine learning model outputs, a technique that has previously been applied to numerical climate models. We also demonstrate substantial gains in computational efficiency: a feedforward neural-network emulator exhibits on the order of 100 times speedup in comparison to the numerical sea-level equation solver that is used for training.

Classifying X-ray Binaries: A Probabilistic Approach

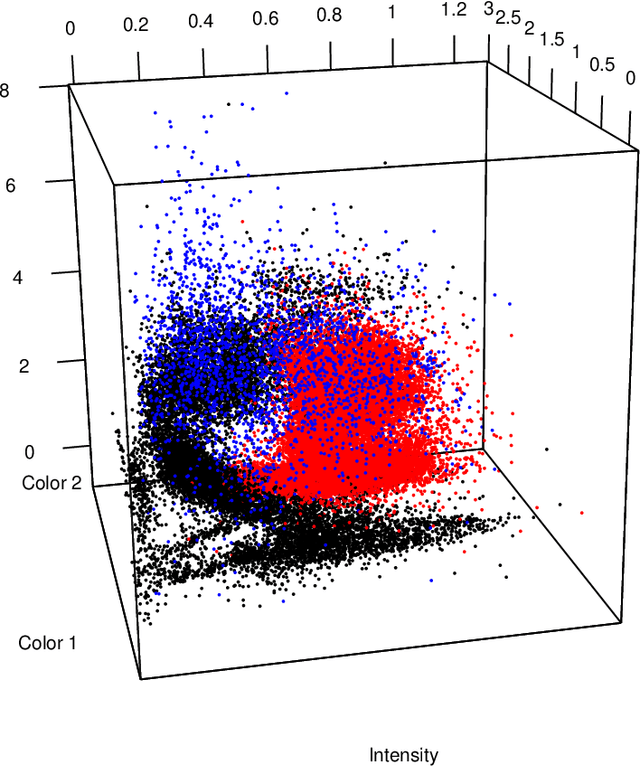
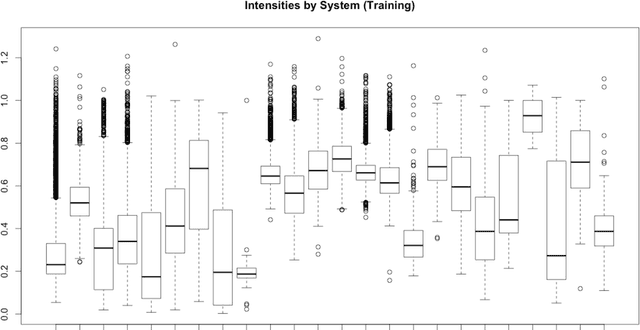
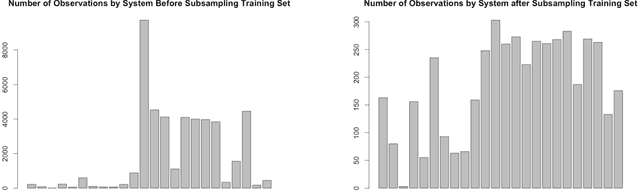
In X-ray binary star systems consisting of a compact object that accretes material from an orbiting secondary star, there is no straightforward means to decide if the compact object is a black hole or a neutron star. To assist this classification, we develop a Bayesian statistical model that makes use of the fact that X-ray binary systems appear to cluster based on their compact object type when viewed from a 3-dimensional coordinate system derived from X-ray spectral data. The first coordinate of this data is the ratio of counts in mid to low energy band (color 1), the second coordinate is the ratio of counts in high to low energy band (color 2), and the third coordinate is the sum of counts in all three bands. We use this model to estimate the probabilities that an X-ray binary system contains a black hole, non-pulsing neutron star, or pulsing neutron star. In particular, we utilize a latent variable model in which the latent variables follow a Gaussian process prior distribution, and hence we are able to induce the spatial correlation we believe exists between systems of the same type. The utility of this approach is evidenced by the accurate prediction of system types using Rossi X-ray Timing Explorer All Sky Monitor data, but it is not flawless. In particular, non-pulsing neutron systems containing "bursters" that are close to the boundary demarcating systems containing black holes tend to be classified as black hole systems. As a byproduct of our analyses, we provide the astronomer with public R code that can be used to predict the compact object type of X-ray binaries given training data.

Admissibility of a posterior predictive decision rule

Recent decades have seen an interest in prediction problems for which Bayesian methodology has been used ubiquitously. Sampling from or approximating the posterior predictive distribution in a Bayesian model allows one to make inferential statements about potentially observable random quantities given observed data. The purpose of this note is to use statistical decision theory as a basis to justify the use of a posterior predictive distribution for making a point prediction.

Quantification of observed prior and likelihood information in parametric Bayesian modeling

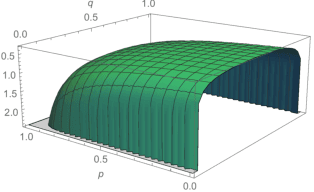
Two data-dependent information metrics are developed to quantify the information of the prior and likelihood functions within a parametric Bayesian model, one of which is closely related to the reference priors from Berger, Bernardo, and Sun, and information measure introduced by Lindley. A combination of theoretical, empirical, and computational support provides evidence that these information-theoretic metrics may be useful diagnostic tools when performing a Bayesian analysis.