Inverse Bayesian Optimization: Learning Human Search Strategies in a Sequential Optimization Task

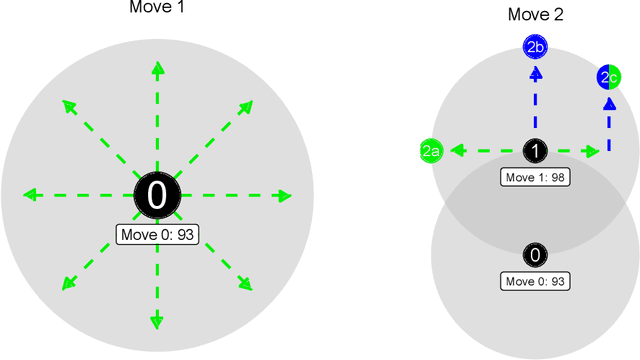
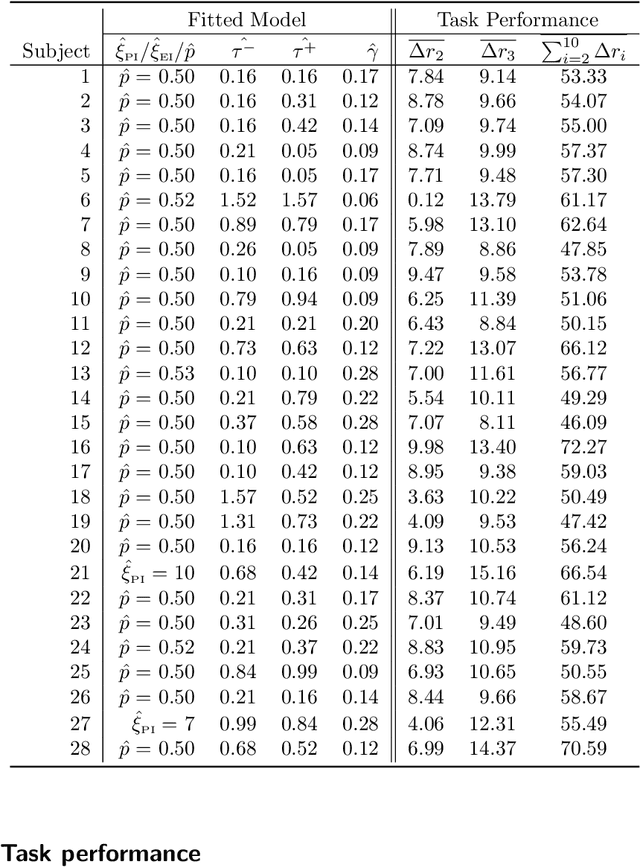
Bayesian optimization is a popular algorithm for sequential optimization of a latent objective function when sampling from the objective is costly. The search path of the algorithm is governed by the acquisition function, which defines the agent's search strategy. Conceptually, the acquisition function characterizes how the optimizer balances exploration and exploitation when searching for the optimum of the latent objective. In this paper, we explore the inverse problem of Bayesian optimization; we seek to estimate the agent's latent acquisition function based on observed search paths. We introduce a probabilistic solution framework for the inverse problem which provides a principled framework to quantify both the variability with which the agent performs the optimization task as well as the uncertainty around their estimated acquisition function. We illustrate our methods by analyzing human behavior from an experiment which was designed to force subjects to balance exploration and exploitation in search of an invisible target location. We find that while most subjects demonstrate clear trends in their search behavior, there is significant variation around these trends from round to round. A wide range of search strategies are exhibited across the subjects in our study, but upper confidence bound acquisition functions offer the best fit for the majority of subjects. Finally, some subjects do not map well to any of the acquisition functions we initially consider; these subjects tend to exhibit exploration preferences beyond that of standard acquisition functions to capture. Guided by the model discrepancies, we augment the candidate acquisition functions to yield a superior fit to the human behavior in this task.

A framework for the fine-grained evaluation of the instantaneous expected value of soccer possessions

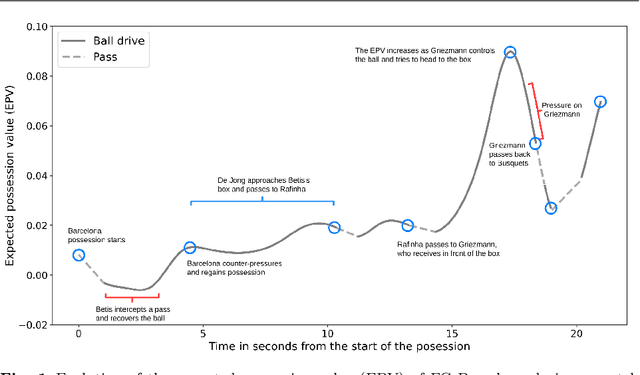
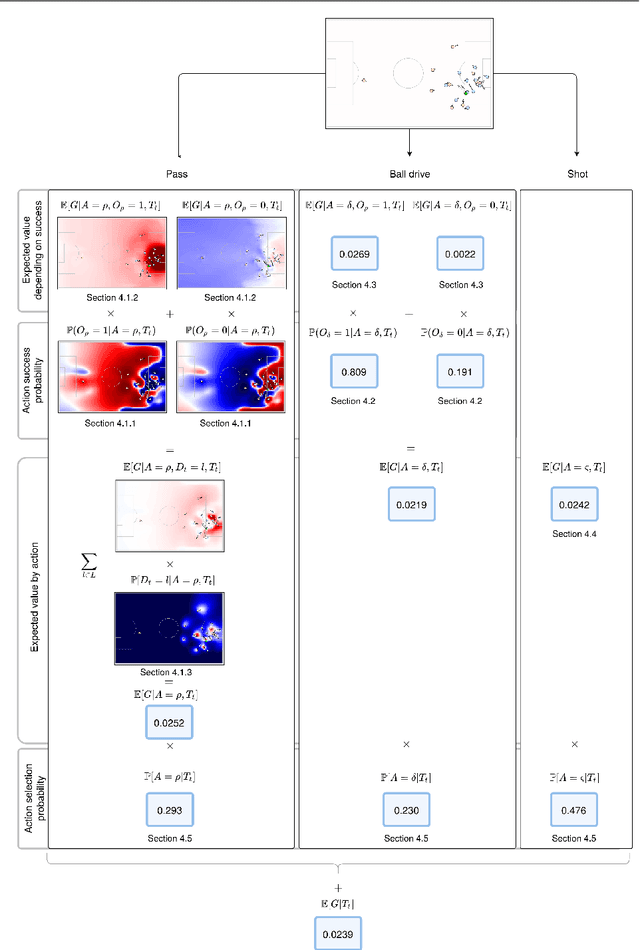
The expected possession value (EPV) of a soccer possession represents the likelihood of a team scoring or receiving the next goal at any time instance. By decomposing the EPV into a series of subcomponents that are estimated separately, we develop a comprehensive analysis framework providing soccer practitioners with the ability to evaluate the impact of both observed and potential actions. We show we can obtain calibrated models for all the components of EPV, including a set of yet-unexplored problems in soccer. We produce visually-interpretable probability surfaces for potential passes from a series of deep neural network architectures that learn from low-level spatiotemporal data. Additionally, we present a series of novel practical applications providing coaches with an enriched interpretation of specific game situations.

SoccerMap: A Deep Learning Architecture for Visually-Interpretable Analysis in Soccer

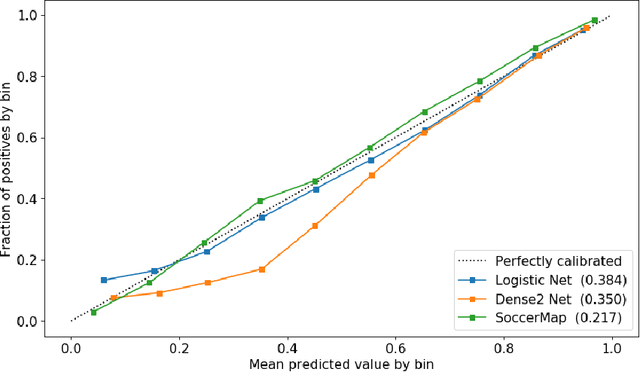
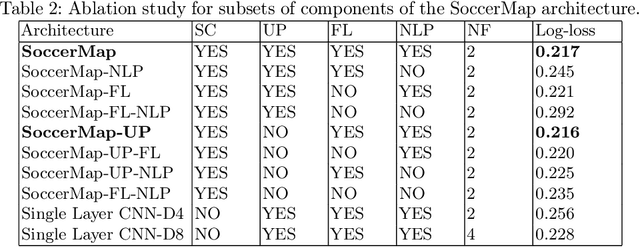
We present a fully convolutional neural network architecture that is capable of estimating full probability surfaces of potential passes in soccer, derived from high-frequency spatiotemporal data. The network receives layers of low-level inputs and learns a feature hierarchy that produces predictions at different sampling levels, capturing both coarse and fine spatial details. By merging these predictions, we can produce visually-rich probability surfaces for any game situation that allows coaches to develop a fine-grained analysis of players' positioning and decision-making, an as-yet little-explored area in sports. We show the network can perform remarkably well in the estimation of pass success probability, and present how it can be adapted easily to approach two other challenging problems: the estimation of pass-selection likelihood and the prediction of the expected value of a pass. Our approach provides a novel solution for learning a full prediction surface when there is only a single-pixel correspondence between ground-truth outcomes and the predicted probability map. The flexibility of this architecture allows its adaptation to a great variety of practical problems in soccer. We also present a set of practical applications, including the evaluation of passing risk at a player level, the identification of the best potential passing options, and the differentiation of passing tendencies between teams.

Classifying X-ray Binaries: A Probabilistic Approach

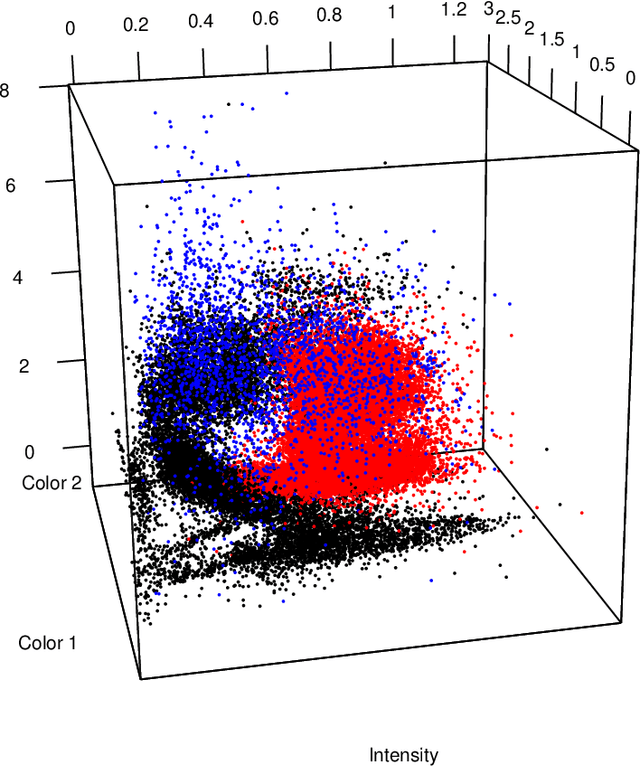
In X-ray binary star systems consisting of a compact object that accretes material from an orbiting secondary star, there is no straightforward means to decide if the compact object is a black hole or a neutron star. To assist this classification, we develop a Bayesian statistical model that makes use of the fact that X-ray binary systems appear to cluster based on their compact object type when viewed from a 3-dimensional coordinate system derived from X-ray spectral data. The first coordinate of this data is the ratio of counts in mid to low energy band (color 1), the second coordinate is the ratio of counts in high to low energy band (color 2), and the third coordinate is the sum of counts in all three bands. We use this model to estimate the probabilities that an X-ray binary system contains a black hole, non-pulsing neutron star, or pulsing neutron star. In particular, we utilize a latent variable model in which the latent variables follow a Gaussian process prior distribution, and hence we are able to induce the spatial correlation we believe exists between systems of the same type. The utility of this approach is evidenced by the accurate prediction of system types using Rossi X-ray Timing Explorer All Sky Monitor data, but it is not flawless. In particular, non-pulsing neutron systems containing "bursters" that are close to the boundary demarcating systems containing black holes tend to be classified as black hole systems. As a byproduct of our analyses, we provide the astronomer with public R code that can be used to predict the compact object type of X-ray binaries given training data.

Time Perception Machine: Temporal Point Processes for the When, Where and What of Activity Prediction

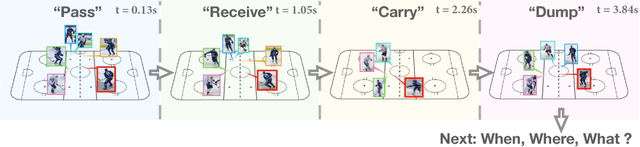
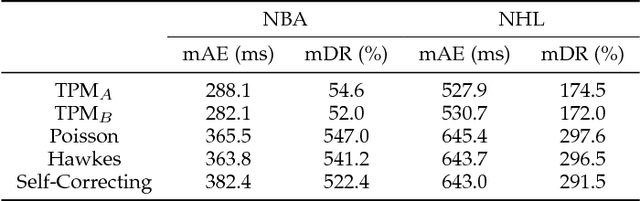
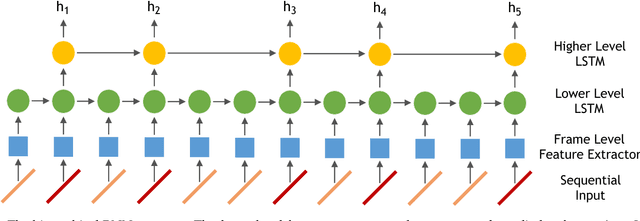
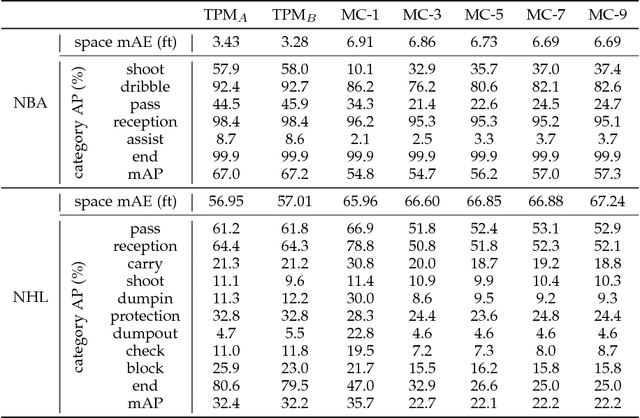
Numerous powerful point process models have been developed to understand temporal patterns in sequential data from fields such as health-care, electronic commerce, social networks, and natural disaster forecasting. In this paper, we develop novel models for learning the temporal distribution of human activities in streaming data (e.g., videos and person trajectories). We propose an integrated framework of neural networks and temporal point processes for predicting when the next activity will happen. Because point processes are limited to taking event frames as input, we propose a simple yet effective mechanism to extract features at frames of interest while also preserving the rich information in the remaining frames. We evaluate our model on two challenging datasets. The results show that our model outperforms traditional statistical point process approaches significantly, demonstrating its effectiveness in capturing the underlying temporal dynamics as well as the correlation within sequential activities. Furthermore, we also extend our model to a joint estimation framework for predicting the timing, spatial location, and category of the activity simultaneously, to answer the when, where, and what of activity prediction.

Learning Person Trajectory Representations for Team Activity Analysis

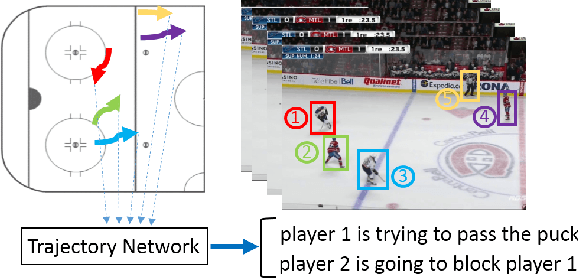
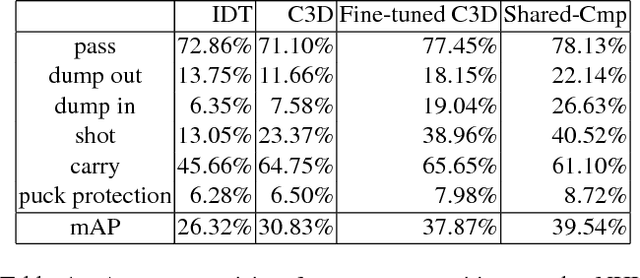
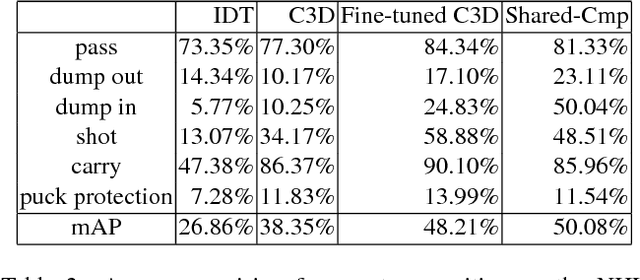
Activity analysis in which multiple people interact across a large space is challenging due to the interplay of individual actions and collective group dynamics. We propose an end-to-end approach for learning person trajectory representations for group activity analysis. The learned representations encode rich spatio-temporal dependencies and capture useful motion patterns for recognizing individual events, as well as characteristic group dynamics that can be used to identify groups from their trajectories alone. We develop our deep learning approach in the context of team sports, which provide well-defined sets of events (e.g. pass, shot) and groups of people (teams). Analysis of events and team formations using NHL hockey and NBA basketball datasets demonstrate the generality of our approach.

Fast and optimal nonparametric sequential design for astronomical observations

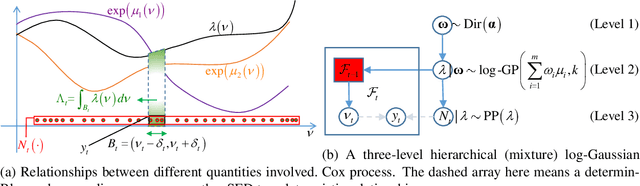
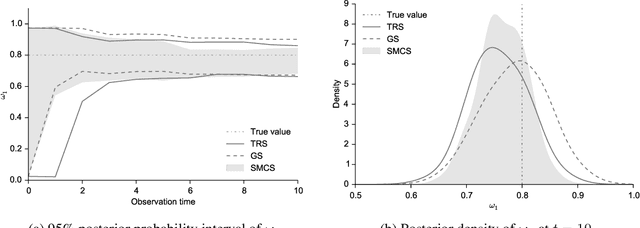
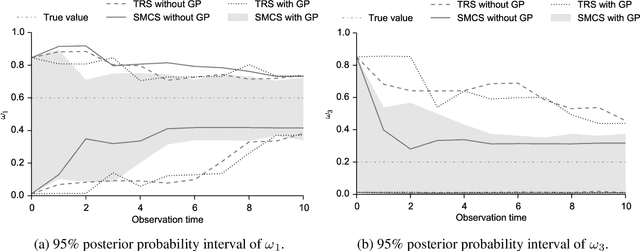
The spectral energy distribution (SED) is a relatively easy way for astronomers to distinguish between different astronomical objects such as galaxies, black holes, and stellar objects. By comparing the observations from a source at different frequencies with template models, astronomers are able to infer the type of this observed object. In this paper, we take a Bayesian model averaging perspective to learn astronomical objects, employing a Bayesian nonparametric approach to accommodate the deviation from convex combinations of known log-SEDs. To effectively use telescope time for observations, we then study Bayesian nonparametric sequential experimental design without conjugacy, in which we use sequential Monte Carlo as an efficient tool to maximize the volume of information stored in the posterior distribution of the parameters of interest. A new technique for performing inferences in log-Gaussian Cox processes called the Poisson log-normal approximation is also proposed. Simulations show the speed, accuracy, and usefulness of our method. While the strategy we propose in this paper is brand new in the astronomy literature, the inferential techniques developed apply to more general nonparametric sequential experimental design problems.

Diversifying Sparsity Using Variational Determinantal Point Processes

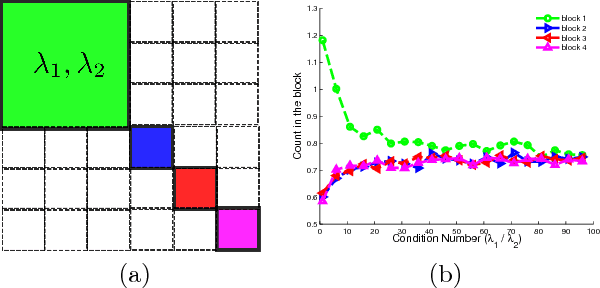
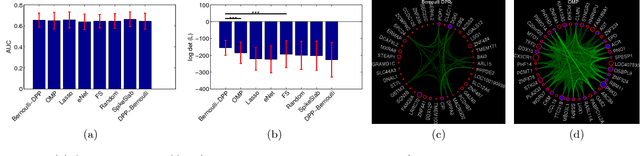
We propose a novel diverse feature selection method based on determinantal point processes (DPPs). Our model enables one to flexibly define diversity based on the covariance of features (similar to orthogonal matching pursuit) or alternatively based on side information. We introduce our approach in the context of Bayesian sparse regression, employing a DPP as a variational approximation to the true spike and slab posterior distribution. We subsequently show how this variational DPP approximation generalizes and extends mean-field approximation, and can be learned efficiently by exploiting the fast sampling properties of DPPs. Our motivating application comes from bioinformatics, where we aim to identify a diverse set of genes whose expression profiles predict a tumor type where the diversity is defined with respect to a gene-gene interaction network. We also explore an application in spatial statistics. In both cases, we demonstrate that the proposed method yields significantly more diverse feature sets than classic sparse methods, without compromising accuracy.

Factorized Point Process Intensities: A Spatial Analysis of Professional Basketball

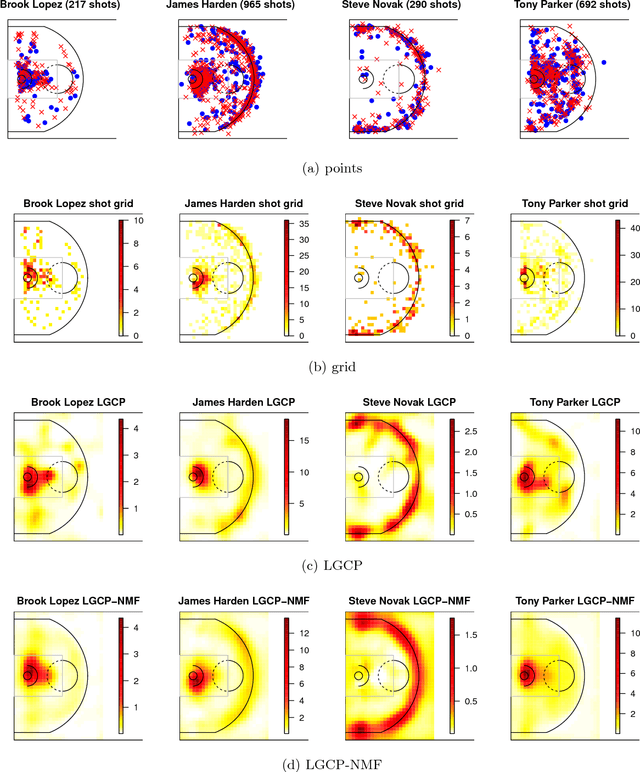
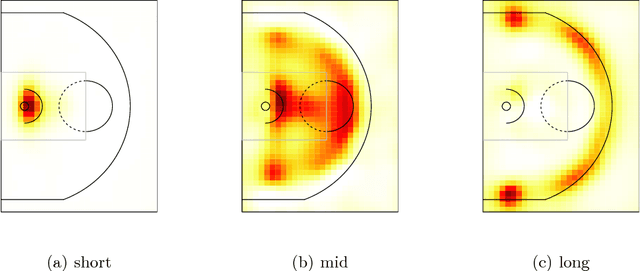
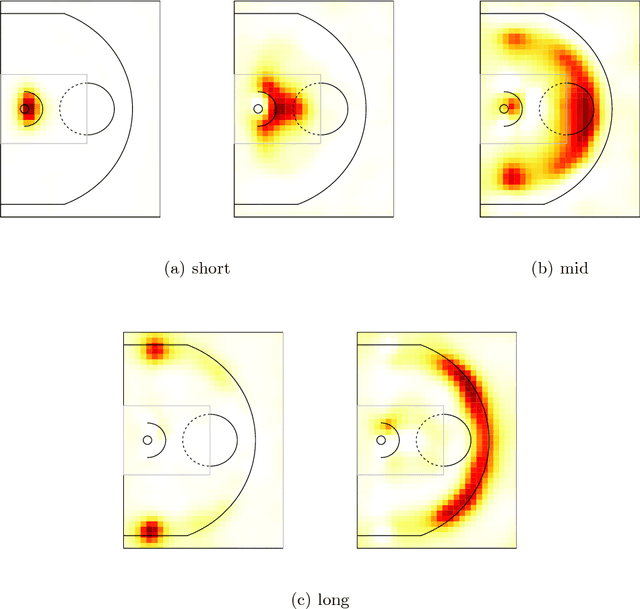
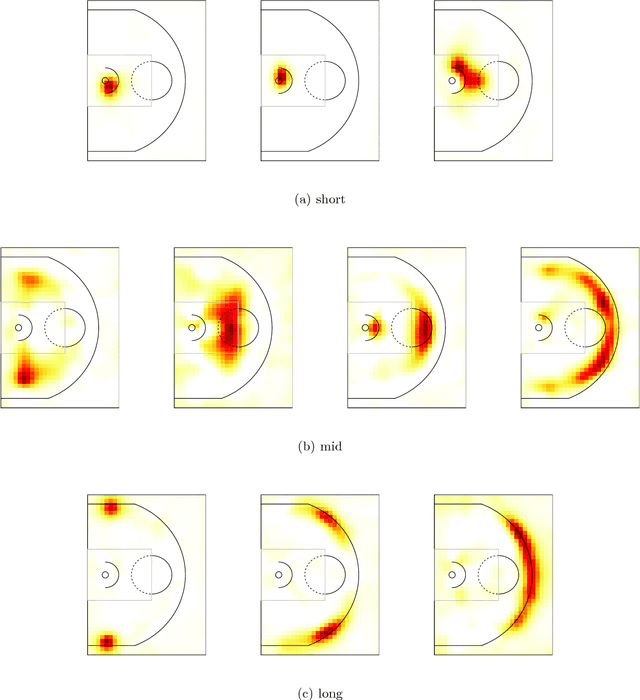
We develop a machine learning approach to represent and analyze the underlying spatial structure that governs shot selection among professional basketball players in the NBA. Typically, NBA players are discussed and compared in an heuristic, imprecise manner that relies on unmeasured intuitions about player behavior. This makes it difficult to draw comparisons between players and make accurate player specific predictions. Modeling shot attempt data as a point process, we create a low dimensional representation of offensive player types in the NBA. Using non-negative matrix factorization (NMF), an unsupervised dimensionality reduction technique, we show that a low-rank spatial decomposition summarizes the shooting habits of NBA players. The spatial representations discovered by the algorithm correspond to intuitive descriptions of NBA player types, and can be used to model other spatial effects, such as shooting accuracy.

Sequential Monte Carlo Bandits

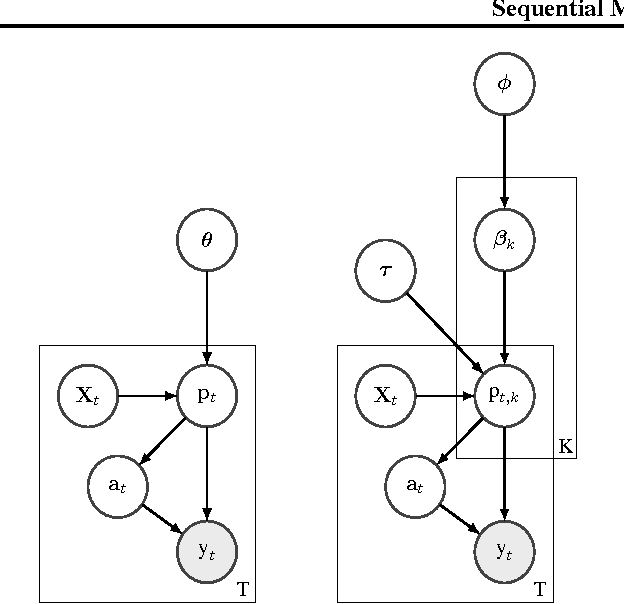
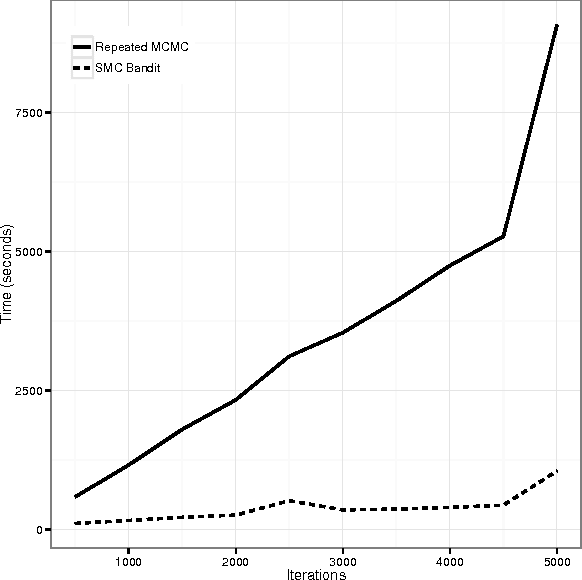
In this paper we propose a flexible and efficient framework for handling multi-armed bandits, combining sequential Monte Carlo algorithms with hierarchical Bayesian modeling techniques. The framework naturally encompasses restless bandits, contextual bandits, and other bandit variants under a single inferential model. Despite the model's generality, we propose efficient Monte Carlo algorithms to make inference scalable, based on recent developments in sequential Monte Carlo methods. Through two simulation studies, the framework is shown to outperform other empirical methods, while also naturally scaling to more complex problems for which existing approaches can not cope. Additionally, we successfully apply our framework to online video-based advertising recommendation, and show its increased efficacy as compared to current state of the art bandit algorithms.