Astromer 2

Foundational models have emerged as a powerful paradigm in deep learning field, leveraging their capacity to learn robust representations from large-scale datasets and effectively to diverse downstream applications such as classification. In this paper, we present Astromer 2 a foundational model specifically designed for extracting light curve embeddings. We introduce Astromer 2 as an enhanced iteration of our self-supervised model for light curve analysis. This paper highlights the advantages of its pre-trained embeddings, compares its performance with that of its predecessor, Astromer 1, and provides a detailed empirical analysis of its capabilities, offering deeper insights into the model's representations. Astromer 2 is pretrained on 1.5 million single-band light curves from the MACHO survey using a self-supervised learning task that predicts randomly masked observations within sequences. Fine-tuning on a smaller labeled dataset allows us to assess its performance in classification tasks. The quality of the embeddings is measured by the F1 score of an MLP classifier trained on Astromer-generated embeddings. Our results demonstrate that Astromer 2 significantly outperforms Astromer 1 across all evaluated scenarios, including limited datasets of 20, 100, and 500 samples per class. The use of weighted per-sample embeddings, which integrate intermediate representations from Astromer's attention blocks, is particularly impactful. Notably, Astromer 2 achieves a 15% improvement in F1 score on the ATLAS dataset compared to prior models, showcasing robust generalization to new datasets. This enhanced performance, especially with minimal labeled data, underscores the potential of Astromer 2 for more efficient and scalable light curve analysis.

Stiff Transfer Learning for Physics-Informed Neural Networks

Stiff differential equations are prevalent in various scientific domains, posing significant challenges due to the disparate time scales of their components. As computational power grows, physics-informed neural networks (PINNs) have led to significant improvements in modeling physical processes described by differential equations. Despite their promising outcomes, vanilla PINNs face limitations when dealing with stiff systems, known as failure modes. In response, we propose a novel approach, stiff transfer learning for physics-informed neural networks (STL-PINNs), to effectively tackle stiff ordinary differential equations (ODEs) and partial differential equations (PDEs). Our methodology involves training a Multi-Head-PINN in a low-stiff regime, and obtaining the final solution in a high stiff regime by transfer learning. This addresses the failure modes related to stiffness in PINNs while maintaining computational efficiency by computing "one-shot" solutions. The proposed approach demonstrates superior accuracy and speed compared to PINNs-based methods, as well as comparable computational efficiency with implicit numerical methods in solving stiff-parameterized linear and polynomial nonlinear ODEs and PDEs under stiff conditions. Furthermore, we demonstrate the scalability of such an approach and the superior speed it offers for simulations involving initial conditions and forcing function reparametrization.

Efficient PINNs: Multi-Head Unimodular Regularization of the Solutions Space

We present a machine learning framework to facilitate the solution of nonlinear multiscale differential equations and, especially, inverse problems using Physics-Informed Neural Networks (PINNs). This framework is based on what is called multihead (MH) training, which involves training the network to learn a general space of all solutions for a given set of equations with certain variability, rather than learning a specific solution of the system. This setup is used with a second novel technique that we call Unimodular Regularization (UR) of the latent space of solutions. We show that the multihead approach, combined with the regularization, significantly improves the efficiency of PINNs by facilitating the transfer learning process thereby enabling the finding of solutions for nonlinear, coupled, and multiscale differential equations.

Exact and approximate error bounds for physics-informed neural networks

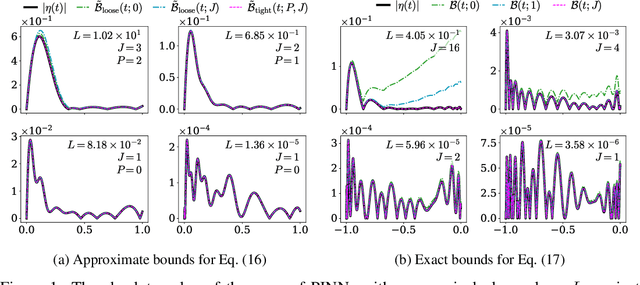
The use of neural networks to solve differential equations, as an alternative to traditional numerical solvers, has increased recently. However, error bounds for the obtained solutions have only been developed for certain equations. In this work, we report important progress in calculating error bounds of physics-informed neural networks (PINNs) solutions of nonlinear first-order ODEs. We give a general expression that describes the error of the solution that the PINN-based method provides for a nonlinear first-order ODE. In addition, we propose a technique to calculate an approximate bound for the general case and an exact bound for a particular case. The error bounds are computed using only the residual information and the equation structure. We apply the proposed methods to particular cases and show that they can successfully provide error bounds without relying on the numerical solution.

Gravitational Duals from Equations of State

Holography relates gravitational theories in five dimensions to four-dimensional quantum field theories in flat space. Under this map, the equation of state of the field theory is encoded in the black hole solutions of the gravitational theory. Solving the five-dimensional Einstein's equations to determine the equation of state is an algorithmic, direct problem. Determining the gravitational theory that gives rise to a prescribed equation of state is a much more challenging, inverse problem. We present a novel approach to solve this problem based on physics-informed neural networks. The resulting algorithm is not only data-driven but also informed by the physics of the Einstein's equations. We successfully apply it to theories with crossovers, first- and second-order phase transitions.

Generating Images of the M87* Black Hole Using GANs

In this paper, we introduce a novel data augmentation methodology based on Conditional Progressive Generative Adversarial Networks (CPGAN) to generate diverse black hole (BH) images, accounting for variations in spin and electron temperature prescriptions. These generated images are valuable resources for training deep learning algorithms to accurately estimate black hole parameters from observational data. Our model can generate BH images for any spin value within the range of [-1, 1], given an electron temperature distribution. To validate the effectiveness of our approach, we employ a convolutional neural network to predict the BH spin using both the GRMHD images and the images generated by our proposed model. Our results demonstrate a significant performance improvement when training is conducted with the augmented dataset while testing is performed using GRMHD simulated data, as indicated by the high R2 score. Consequently, we propose that GANs can be employed as cost effective models for black hole image generation and reliably augment training datasets for other parameterization algorithms.

One-Shot Transfer Learning for Nonlinear ODEs

We introduce a generalizable approach that combines perturbation method and one-shot transfer learning to solve nonlinear ODEs with a single polynomial term, using Physics-Informed Neural Networks (PINNs). Our method transforms non-linear ODEs into linear ODE systems, trains a PINN across varied conditions, and offers a closed-form solution for new instances within the same non-linear ODE class. We demonstrate the effectiveness of this approach on the Duffing equation and suggest its applicability to similarly structured PDEs and ODE systems.

Error-Aware B-PINNs: Improving Uncertainty Quantification in Bayesian Physics-Informed Neural Networks

Physics-Informed Neural Networks (PINNs) are gaining popularity as a method for solving differential equations. While being more feasible in some contexts than the classical numerical techniques, PINNs still lack credibility. A remedy for that can be found in Uncertainty Quantification (UQ) which is just beginning to emerge in the context of PINNs. Assessing how well the trained PINN complies with imposed differential equation is the key to tackling uncertainty, yet there is lack of comprehensive methodology for this task. We propose a framework for UQ in Bayesian PINNs (B-PINNs) that incorporates the discrepancy between the B-PINN solution and the unknown true solution. We exploit recent results on error bounds for PINNs on linear dynamical systems and demonstrate the predictive uncertainty on a class of linear ODEs.

Improving astroBERT using Semantic Textual Similarity

The NASA Astrophysics Data System (ADS) is an essential tool for researchers that allows them to explore the astronomy and astrophysics scientific literature, but it has yet to exploit recent advances in natural language processing. At ADASS 2021, we introduced astroBERT, a machine learning language model tailored to the text used in astronomy papers in ADS. In this work we: - announce the first public release of the astroBERT language model; - show how astroBERT improves over existing public language models on astrophysics specific tasks; - and detail how ADS plans to harness the unique structure of scientific papers, the citation graph and citation context, to further improve astroBERT.

Transfer Learning with Physics-Informed Neural Networks for Efficient Simulation of Branched Flows

Physics-Informed Neural Networks (PINNs) offer a promising approach to solving differential equations and, more generally, to applying deep learning to problems in the physical sciences. We adopt a recently developed transfer learning approach for PINNs and introduce a multi-head model to efficiently obtain accurate solutions to nonlinear systems of ordinary differential equations with random potentials. In particular, we apply the method to simulate stochastic branched flows, a universal phenomenon in random wave dynamics. Finally, we compare the results achieved by feed forward and GAN-based PINNs on two physically relevant transfer learning tasks and show that our methods provide significant computational speedups in comparison to standard PINNs trained from scratch.