Gravitational Duals from Equations of State

Holography relates gravitational theories in five dimensions to four-dimensional quantum field theories in flat space. Under this map, the equation of state of the field theory is encoded in the black hole solutions of the gravitational theory. Solving the five-dimensional Einstein's equations to determine the equation of state is an algorithmic, direct problem. Determining the gravitational theory that gives rise to a prescribed equation of state is a much more challenging, inverse problem. We present a novel approach to solve this problem based on physics-informed neural networks. The resulting algorithm is not only data-driven but also informed by the physics of the Einstein's equations. We successfully apply it to theories with crossovers, first- and second-order phase transitions.

Universal NER: A Gold-Standard Multilingual Named Entity Recognition Benchmark

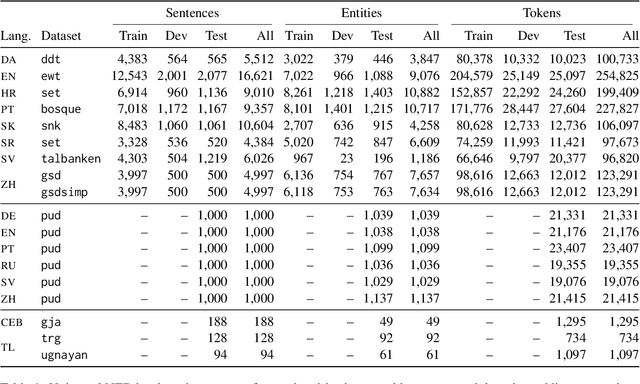
We introduce Universal NER (UNER), an open, community-driven project to develop gold-standard NER benchmarks in many languages. The overarching goal of UNER is to provide high-quality, cross-lingually consistent annotations to facilitate and standardize multilingual NER research. UNER v1 contains 18 datasets annotated with named entities in a cross-lingual consistent schema across 12 diverse languages. In this paper, we detail the dataset creation and composition of UNER; we also provide initial modeling baselines on both in-language and cross-lingual learning settings. We release the data, code, and fitted models to the public.

Do CoNLL-2003 Named Entity Taggers Still Work Well in 2023?

Named Entity Recognition (NER) is an important and well-studied task in natural language processing. The classic CoNLL-2003 English dataset, published almost 20 years ago, is commonly used to train and evaluate named entity taggers. The age of this dataset raises the question of how well these models perform when applied to modern data. In this paper, we present CoNLL++, a new annotated test set that mimics the process used to create the original CoNLL-2003 test set as closely as possible, except with data collected from 2020. Using CoNLL++, we evaluate the generalization of 20+ different models to modern data. We observe that different models have very different generalization behavior. F\textsubscript{1} scores of large transformer-based models which are pre-trained on recent data dropped much less than models using static word embeddings, and RoBERTa-based and T5 models achieve comparable F\textsubscript{1} scores on both CoNLL-2003 and CoNLL++. Our experiments show that achieving good generalizability requires a combined effort of developing larger models and continuing pre-training with in-domain and recent data. These results suggest standard evaluation methodology may have under-estimated progress on named entity recognition over the past 20 years; in addition to improving performance on the original CoNLL-2003 dataset, we have also improved the ability of our models to generalize to modern data.

Evaluating Error Bound for Physics-Informed Neural Networks on Linear Dynamical Systems

There have been extensive studies on solving differential equations using physics-informed neural networks. While this method has proven advantageous in many cases, a major criticism lies in its lack of analytical error bounds. Therefore, it is less credible than its traditional counterparts, such as the finite difference method. This paper shows that one can mathematically derive explicit error bounds for physics-informed neural networks trained on a class of linear systems of differential equations. More importantly, evaluating such error bounds only requires evaluating the differential equation residual infinity norm over the domain of interest. Our work shows a link between network residuals, which is known and used as loss function, and the absolute error of solution, which is generally unknown. Our approach is semi-phenomonological and independent of knowledge of the actual solution or the complexity or architecture of the network. Using the method of manufactured solution on linear ODEs and system of linear ODEs, we empirically verify the error evaluation algorithm and demonstrate that the actual error strictly lies within our derived bound.