Fast and optimal nonparametric sequential design for astronomical observations
Paper and Code
Jan 11, 2015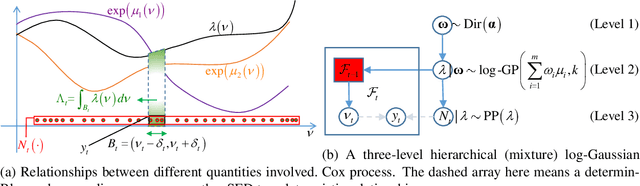
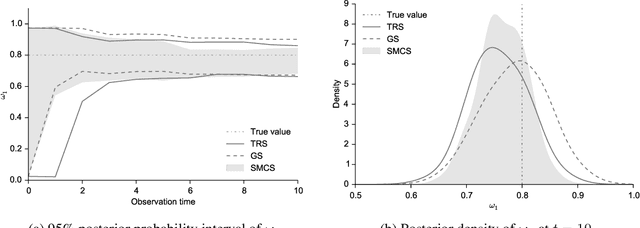
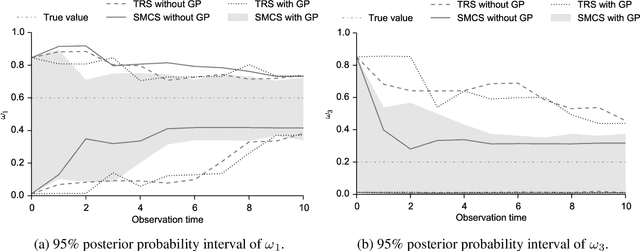

The spectral energy distribution (SED) is a relatively easy way for astronomers to distinguish between different astronomical objects such as galaxies, black holes, and stellar objects. By comparing the observations from a source at different frequencies with template models, astronomers are able to infer the type of this observed object. In this paper, we take a Bayesian model averaging perspective to learn astronomical objects, employing a Bayesian nonparametric approach to accommodate the deviation from convex combinations of known log-SEDs. To effectively use telescope time for observations, we then study Bayesian nonparametric sequential experimental design without conjugacy, in which we use sequential Monte Carlo as an efficient tool to maximize the volume of information stored in the posterior distribution of the parameters of interest. A new technique for performing inferences in log-Gaussian Cox processes called the Poisson log-normal approximation is also proposed. Simulations show the speed, accuracy, and usefulness of our method. While the strategy we propose in this paper is brand new in the astronomy literature, the inferential techniques developed apply to more general nonparametric sequential experimental design problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge