Diversifying Sparsity Using Variational Determinantal Point Processes
Paper and Code
Nov 23, 2014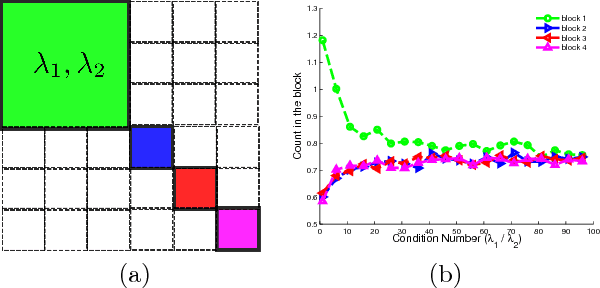
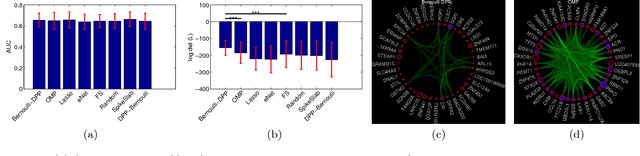

We propose a novel diverse feature selection method based on determinantal point processes (DPPs). Our model enables one to flexibly define diversity based on the covariance of features (similar to orthogonal matching pursuit) or alternatively based on side information. We introduce our approach in the context of Bayesian sparse regression, employing a DPP as a variational approximation to the true spike and slab posterior distribution. We subsequently show how this variational DPP approximation generalizes and extends mean-field approximation, and can be learned efficiently by exploiting the fast sampling properties of DPPs. Our motivating application comes from bioinformatics, where we aim to identify a diverse set of genes whose expression profiles predict a tumor type where the diversity is defined with respect to a gene-gene interaction network. We also explore an application in spatial statistics. In both cases, we demonstrate that the proposed method yields significantly more diverse feature sets than classic sparse methods, without compromising accuracy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge