Spatiotemporal Density Correction of Multivariate Global Climate Model Projections using Deep Learning

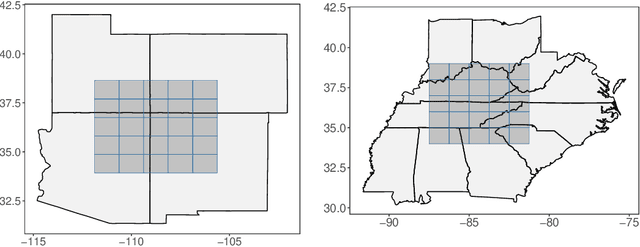
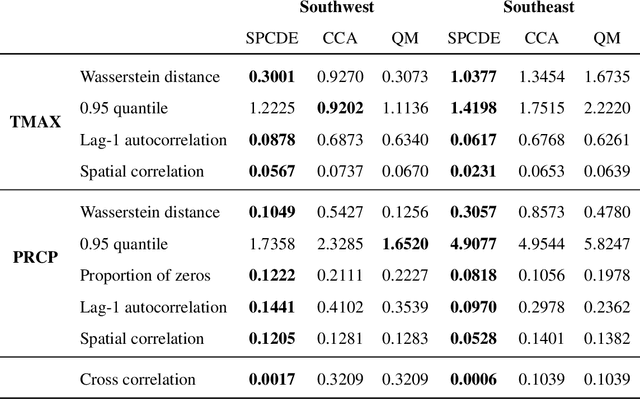
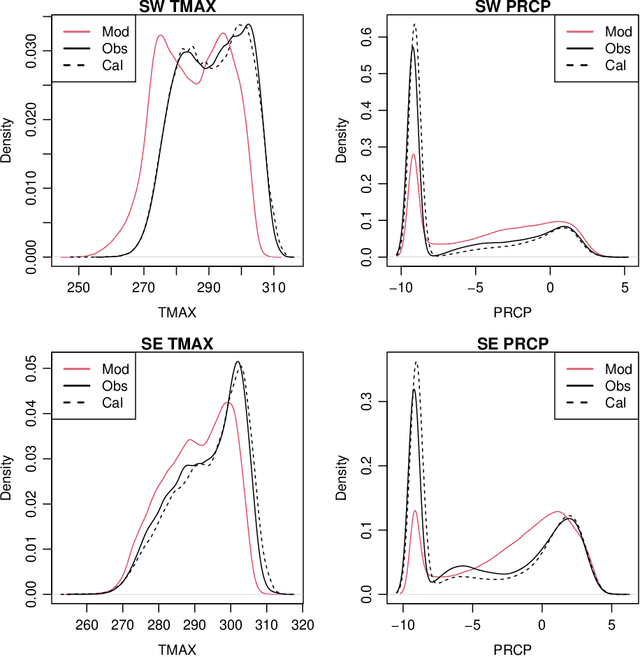
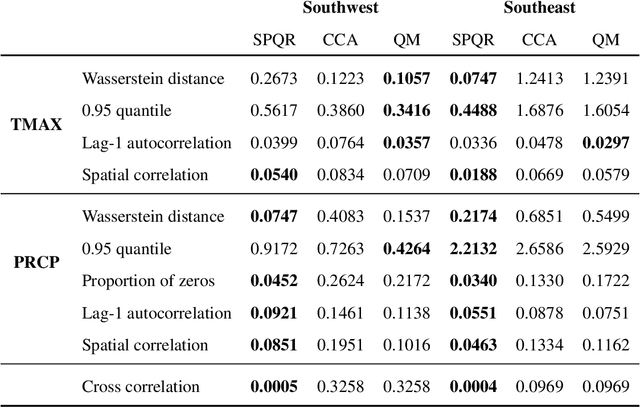
Global Climate Models (GCMs) are numerical models that simulate complex physical processes within the Earth's climate system and are essential for understanding and predicting climate change. However, GCMs suffer from systemic biases due to simplifications made to the underlying physical processes. GCM output therefore needs to be bias corrected before it can be used for future climate projections. Most common bias correction methods, however, cannot preserve spatial, temporal, or inter-variable dependencies. We propose a new semi-parametric conditional density estimation (SPCDE) for density correction of the joint distribution of daily precipitation and maximum temperature data obtained from gridded GCM spatial fields. The Vecchia approximation is employed to preserve dependencies in the observed field during the density correction process, which is carried out using semi-parametric quantile regression. The ability to calibrate joint distributions of GCM projections has potential advantages not only in estimating extremes, but also in better estimating compound hazards, like heat waves and drought, under potential climate change. Illustration on historical data from 1951-2014 over two 5x5 spatial grids in the US indicate that SPCDE can preserve key marginal and joint distribution properties of precipitation and maximum temperature, and predictions obtained using SPCDE are better calibrated compared to predictions using asynchronous quantile mapping and canonical correlation analysis, two commonly used bias correction approaches.

Amortized Bayesian Local Interpolation NetworK: Fast covariance parameter estimation for Gaussian Processes

Gaussian processes (GPs) are a ubiquitous tool for geostatistical modeling with high levels of flexibility and interpretability, and the ability to make predictions at unseen spatial locations through a process called Kriging. Estimation of Kriging weights relies on the inversion of the process' covariance matrix, creating a computational bottleneck for large spatial datasets. In this paper, we propose an Amortized Bayesian Local Interpolation NetworK (A-BLINK) for fast covariance parameter estimation, which uses two pre-trained deep neural networks to learn a mapping from spatial location coordinates and covariance function parameters to Kriging weights and the spatial variance, respectively. The fast prediction time of these networks allows us to bypass the matrix inversion step, creating large computational speedups over competing methods in both frequentist and Bayesian settings, and also provides full posterior inference and predictions using Markov chain Monte Carlo sampling methods. We show significant increases in computational efficiency over comparable scalable GP methodology in an extensive simulation study with lower parameter estimation error. The efficacy of our approach is also demonstrated using a temperature dataset of US climate normals for 1991--2020 based on over 7,000 weather stations.

Deep Learning of Multivariate Extremes via a Geometric Representation

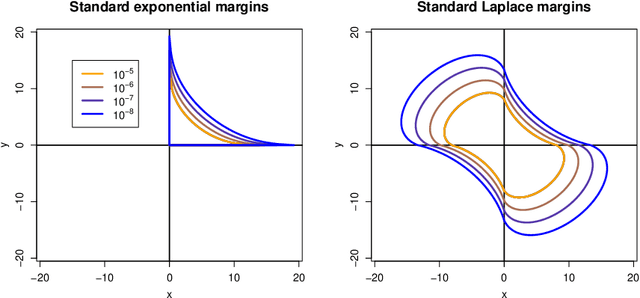
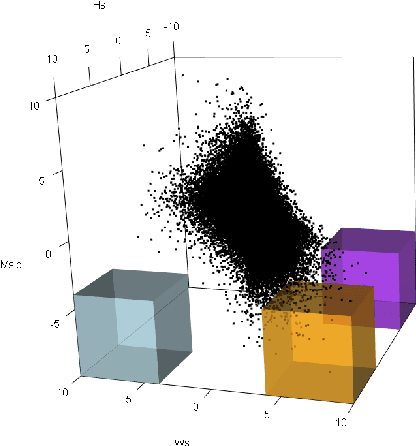
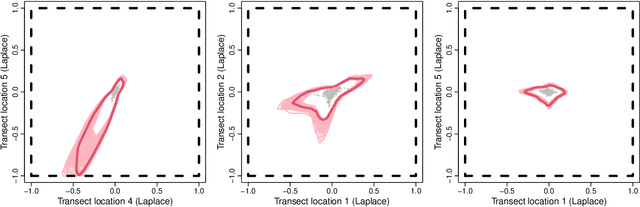
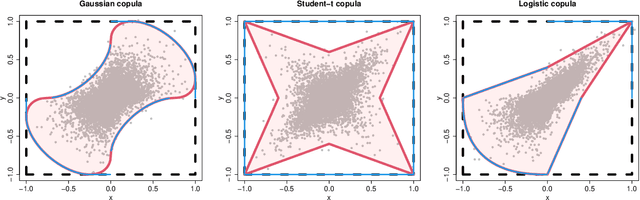
The study of geometric extremes, where extremal dependence properties are inferred from the deterministic limiting shapes of scaled sample clouds, provides an exciting approach to modelling the extremes of multivariate data. These shapes, termed limit sets, link together several popular extremal dependence modelling frameworks. Although the geometric approach is becoming an increasingly popular modelling tool, current inference techniques are limited to a low dimensional setting (d < 4), and generally require rigid modelling assumptions. In this work, we propose a range of novel theoretical results to aid with the implementation of the geometric extremes framework and introduce the first approach to modelling limit sets using deep learning. By leveraging neural networks, we construct asymptotically-justified yet flexible semi-parametric models for extremal dependence of high-dimensional data. We showcase the efficacy of our deep approach by modelling the complex extremal dependencies between meteorological and oceanographic variables in the North Sea off the coast of the UK.

SPQR: An R Package for Semi-Parametric Density and Quantile Regression

We develop an R package SPQR that implements the semi-parametric quantile regression (SPQR) method in Xu and Reich (2021). The method begins by fitting a flexible density regression model using monotonic splines whose weights are modeled as data-dependent functions using artificial neural networks. Subsequently, estimates of conditional density and quantile process can all be obtained. Unlike many approaches to quantile regression that assume a linear model, SPQR allows for virtually any relationship between the covariates and the response distribution including non-linear effects and different effects on different quantile levels. To increase the interpretability and transparency of SPQR, model-agnostic statistics developed by Apley and Zhu (2020) are used to estimate and visualize the covariate effects and their relative importance on the quantile function. In this article, we detail how this framework is implemented in SPQR and illustrate how this package should be used in practice through simulated and real data examples.