When the whole is greater than the sum of its parts: Scaling black-box inference to large data settings through divide-and-conquer

Black-box methods such as deep neural networks are exceptionally fast at obtaining point estimates of model parameters due to their amortisation of the loss function computation, but are currently restricted to settings for which simulating training data is inexpensive. When simulating data is computationally expensive, both the training and uncertainty quantification, which typically relies on a parametric bootstrap, become intractable. We propose a black-box divide-and-conquer estimation and inference framework when data simulation is computationally expensive that trains a black-box estimation method on a partition of the multivariate data domain, estimates and bootstraps on the partitioned data, and combines estimates and inferences across data partitions. Through the divide step, only small training data need be simulated, substantially accelerating the training. Further, the estimation and bootstrapping can be conducted in parallel across multiple computing nodes to further speed up the procedure. Finally, the conquer step accounts for any dependence between data partitions through a statistically and computationally efficient weighted average. We illustrate the implementation of our framework in high-dimensional spatial settings with Gaussian and max-stable processes. Applications to modeling extremal temperature data from both a climate model and observations from the National Oceanic and Atmospheric Administration highlight the feasibility of estimation and inference of max-stable process parameters with tens of thousands of locations.

Spatiotemporal Density Correction of Multivariate Global Climate Model Projections using Deep Learning

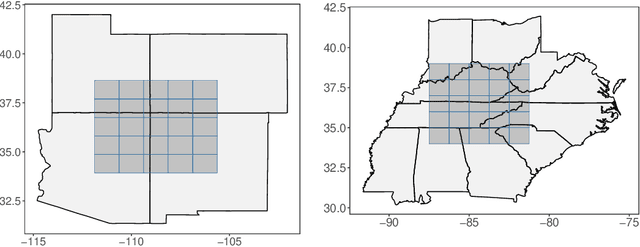
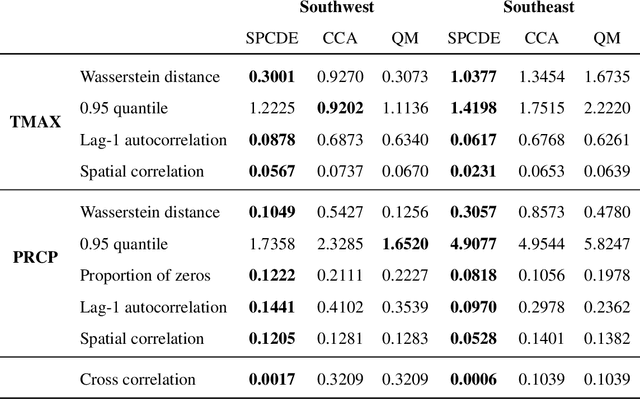
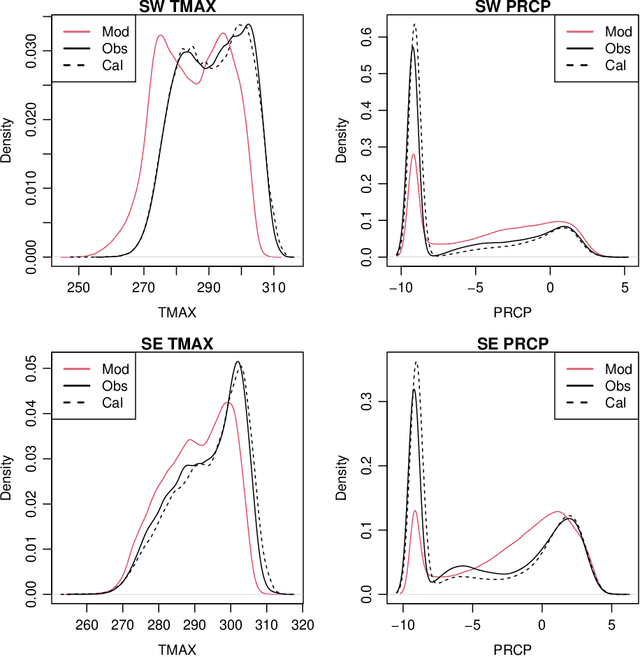
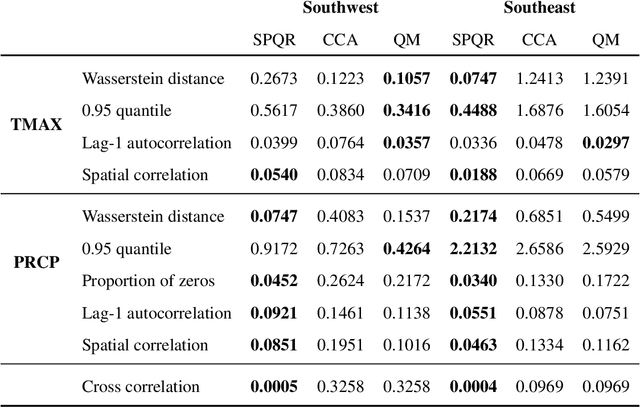
Global Climate Models (GCMs) are numerical models that simulate complex physical processes within the Earth's climate system and are essential for understanding and predicting climate change. However, GCMs suffer from systemic biases due to simplifications made to the underlying physical processes. GCM output therefore needs to be bias corrected before it can be used for future climate projections. Most common bias correction methods, however, cannot preserve spatial, temporal, or inter-variable dependencies. We propose a new semi-parametric conditional density estimation (SPCDE) for density correction of the joint distribution of daily precipitation and maximum temperature data obtained from gridded GCM spatial fields. The Vecchia approximation is employed to preserve dependencies in the observed field during the density correction process, which is carried out using semi-parametric quantile regression. The ability to calibrate joint distributions of GCM projections has potential advantages not only in estimating extremes, but also in better estimating compound hazards, like heat waves and drought, under potential climate change. Illustration on historical data from 1951-2014 over two 5x5 spatial grids in the US indicate that SPCDE can preserve key marginal and joint distribution properties of precipitation and maximum temperature, and predictions obtained using SPCDE are better calibrated compared to predictions using asynchronous quantile mapping and canonical correlation analysis, two commonly used bias correction approaches.

Multivariate and Online Transfer Learning with Uncertainty Quantification

Untreated periodontitis causes inflammation within the supporting tissue of the teeth and can ultimately lead to tooth loss. Modeling periodontal outcomes is beneficial as they are difficult and time consuming to measure, but disparities in representation between demographic groups must be considered. There may not be enough participants to build group specific models and it can be ineffective, and even dangerous, to apply a model to participants in an underrepresented group if demographic differences were not considered during training. We propose an extension to RECaST Bayesian transfer learning framework. Our method jointly models multivariate outcomes, exhibiting significant improvement over the previous univariate RECaST method. Further, we introduce an online approach to model sequential data sets. Negative transfer is mitigated to ensure that the information shared from the other demographic groups does not negatively impact the modeling of the underrepresented participants. The Bayesian framework naturally provides uncertainty quantification on predictions. Especially important in medical applications, our method does not share data between domains. We demonstrate the effectiveness of our method in both predictive performance and uncertainty quantification on simulated data and on a database of dental records from the HealthPartners Institute.

A variational neural Bayes framework for inference on intractable posterior distributions

Classic Bayesian methods with complex models are frequently infeasible due to an intractable likelihood. Simulation-based inference methods, such as Approximate Bayesian Computing (ABC), calculate posteriors without accessing a likelihood function by leveraging the fact that data can be quickly simulated from the model, but converge slowly and/or poorly in high-dimensional settings. In this paper, we propose a framework for Bayesian posterior estimation by mapping data to posteriors of parameters using a neural network trained on data simulated from the complex model. Posterior distributions of model parameters are efficiently obtained by feeding observed data into the trained neural network. We show theoretically that our posteriors converge to the true posteriors in Kullback-Leibler divergence. Our approach yields computationally efficient and theoretically justified uncertainty quantification, which is lacking in existing simulation-based neural network approaches. Comprehensive simulation studies highlight our method's robustness and accuracy.

A statistical framework for GWAS of high dimensional phenotypes using summary statistics, with application to metabolite GWAS

The recent explosion of genetic and high dimensional biobank and 'omic' data has provided researchers with the opportunity to investigate the shared genetic origin (pleiotropy) of hundreds to thousands of related phenotypes. However, existing methods for multi-phenotype genome-wide association studies (GWAS) do not model pleiotropy, are only applicable to a small number of phenotypes, or provide no way to perform inference. To add further complication, raw genetic and phenotype data are rarely observed, meaning analyses must be performed on GWAS summary statistics whose statistical properties in high dimensions are poorly understood. We therefore developed a novel model, theoretical framework, and set of methods to perform Bayesian inference in GWAS of high dimensional phenotypes using summary statistics that explicitly model pleiotropy, beget fast computation, and facilitate the use of biologically informed priors. We demonstrate the utility of our procedure by applying it to metabolite GWAS, where we develop new nonparametric priors for genetic effects on metabolite levels that use known metabolic pathway information and foster interpretable inference at the pathway level.

Transfer Learning with Uncertainty Quantification: Random Effect Calibration of Source to Target (RECaST)

Transfer learning uses a data model, trained to make predictions or inferences on data from one population, to make reliable predictions or inferences on data from another population. Most existing transfer learning approaches are based on fine-tuning pre-trained neural network models, and fail to provide crucial uncertainty quantification. We develop a statistical framework for model predictions based on transfer learning, called RECaST. The primary mechanism is a Cauchy random effect that recalibrates a source model to a target population; we mathematically and empirically demonstrate the validity of our RECaST approach for transfer learning between linear models, in the sense that prediction sets will achieve their nominal stated coverage, and we numerically illustrate the method's robustness to asymptotic approximations for nonlinear models. Whereas many existing techniques are built on particular source models, RECaST is agnostic to the choice of source model. For example, our RECaST transfer learning approach can be applied to a continuous or discrete data model with linear or logistic regression, deep neural network architectures, etc. Furthermore, RECaST provides uncertainty quantification for predictions, which is mostly absent in the literature. We examine our method's performance in a simulation study and in an application to real hospital data.