When the whole is greater than the sum of its parts: Scaling black-box inference to large data settings through divide-and-conquer

Black-box methods such as deep neural networks are exceptionally fast at obtaining point estimates of model parameters due to their amortisation of the loss function computation, but are currently restricted to settings for which simulating training data is inexpensive. When simulating data is computationally expensive, both the training and uncertainty quantification, which typically relies on a parametric bootstrap, become intractable. We propose a black-box divide-and-conquer estimation and inference framework when data simulation is computationally expensive that trains a black-box estimation method on a partition of the multivariate data domain, estimates and bootstraps on the partitioned data, and combines estimates and inferences across data partitions. Through the divide step, only small training data need be simulated, substantially accelerating the training. Further, the estimation and bootstrapping can be conducted in parallel across multiple computing nodes to further speed up the procedure. Finally, the conquer step accounts for any dependence between data partitions through a statistically and computationally efficient weighted average. We illustrate the implementation of our framework in high-dimensional spatial settings with Gaussian and max-stable processes. Applications to modeling extremal temperature data from both a climate model and observations from the National Oceanic and Atmospheric Administration highlight the feasibility of estimation and inference of max-stable process parameters with tens of thousands of locations.

A variational neural Bayes framework for inference on intractable posterior distributions

Classic Bayesian methods with complex models are frequently infeasible due to an intractable likelihood. Simulation-based inference methods, such as Approximate Bayesian Computing (ABC), calculate posteriors without accessing a likelihood function by leveraging the fact that data can be quickly simulated from the model, but converge slowly and/or poorly in high-dimensional settings. In this paper, we propose a framework for Bayesian posterior estimation by mapping data to posteriors of parameters using a neural network trained on data simulated from the complex model. Posterior distributions of model parameters are efficiently obtained by feeding observed data into the trained neural network. We show theoretically that our posteriors converge to the true posteriors in Kullback-Leibler divergence. Our approach yields computationally efficient and theoretically justified uncertainty quantification, which is lacking in existing simulation-based neural network approaches. Comprehensive simulation studies highlight our method's robustness and accuracy.

Neural Likelihood Surfaces for Spatial Processes with Computationally Intensive or Intractable Likelihoods

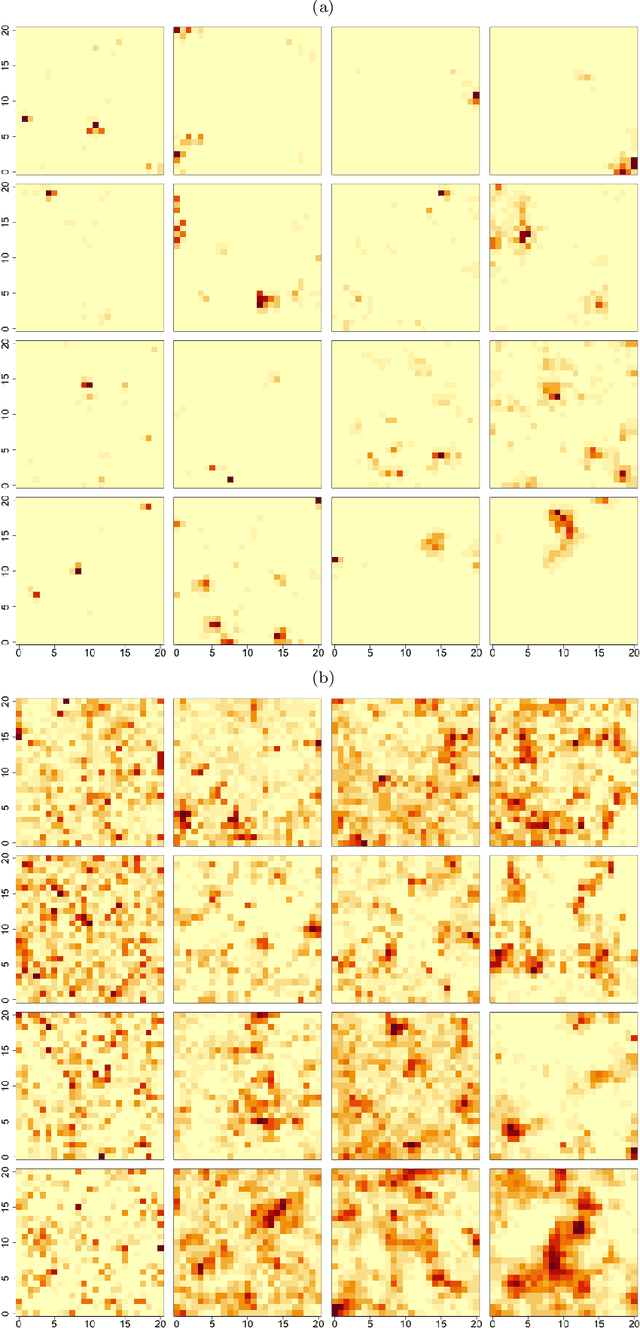
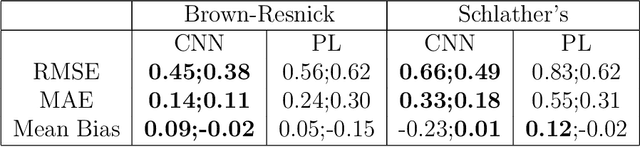
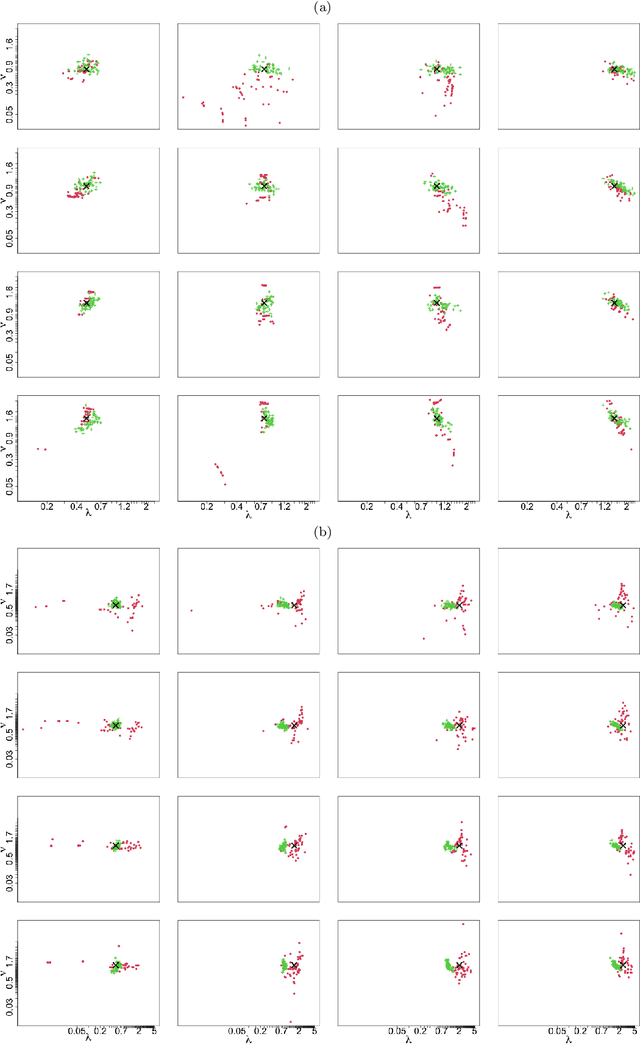
In spatial statistics, fast and accurate parameter estimation coupled with a reliable means of uncertainty quantification can be a challenging task when fitting a spatial process to real-world data because the likelihood function might be slow to evaluate or intractable. In this work, we propose using convolutional neural networks (CNNs) to learn the likelihood function of a spatial process. Through a specifically designed classification task, our neural network implicitly learns the likelihood function, even in situations where the exact likelihood is not explicitly available. Once trained on the classification task, our neural network is calibrated using Platt scaling which improves the accuracy of the neural likelihood surfaces. To demonstrate our approach, we compare maximum likelihood estimates and approximate confidence regions constructed from the neural likelihood surface with the equivalent for exact or approximate likelihood for two different spatial processes: a Gaussian Process, which has a computationally intensive likelihood function for large datasets, and a Brown-Resnick Process, which has an intractable likelihood function. We also compare the neural likelihood surfaces to the exact and approximate likelihood surfaces for the Gaussian Process and Brown-Resnick Process, respectively. We conclude that our method provides fast and accurate parameter estimation with a reliable method of uncertainty quantification in situations where standard methods are either undesirably slow or inaccurate.

Towards black-box parameter estimation

Deep learning algorithms have recently shown to be a successful tool in estimating parameters of statistical models for which simulation is easy, but likelihood computation is challenging. But the success of these approaches depends on simulating parameters that sufficiently reproduce the observed data, and, at present, there is a lack of efficient methods to produce these simulations. We develop new black-box procedures to estimate parameters of statistical models based only on weak parameter structure assumptions. For well-structured likelihoods with frequent occurrences, such as in time series, this is achieved by pre-training a deep neural network on an extensive simulated database that covers a wide range of data sizes. For other types of complex dependencies, an iterative algorithm guides simulations to the correct parameter region in multiple rounds. These approaches can successfully estimate and quantify the uncertainty of parameters from non-Gaussian models with complex spatial and temporal dependencies. The success of our methods is a first step towards a fully flexible automatic black-box estimation framework.

Neural Networks for Parameter Estimation in Intractable Models

We propose to use deep learning to estimate parameters in statistical models when standard likelihood estimation methods are computationally infeasible. We show how to estimate parameters from max-stable processes, where inference is exceptionally challenging even with small datasets but simulation is straightforward. We use data from model simulations as input and train deep neural networks to learn statistical parameters. Our neural-network-based method provides a competitive alternative to current approaches, as demonstrated by considerable accuracy and computational time improvements. It serves as a proof of concept for deep learning in statistical parameter estimation and can be extended to other estimation problems.

Parameter Estimation with Dense and Convolutional Neural Networks Applied to the FitzHugh-Nagumo ODE

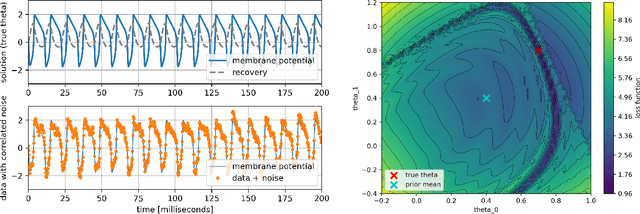
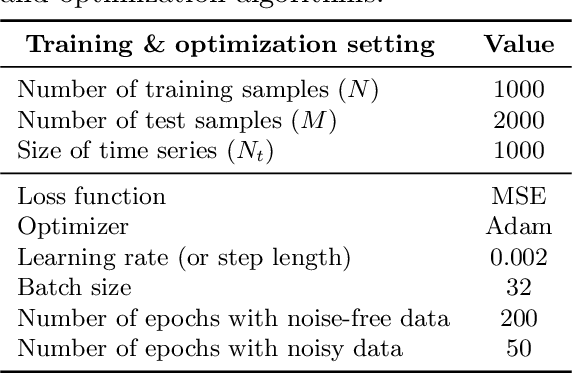
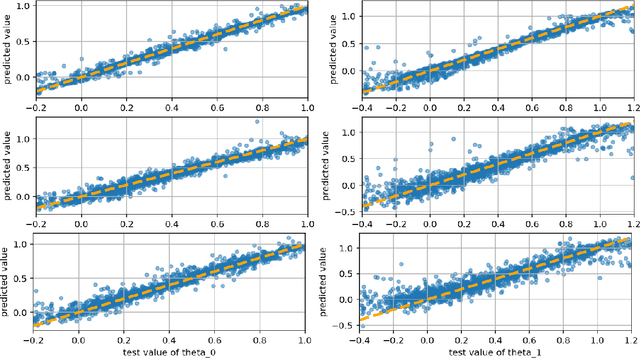
Machine learning algorithms have been successfully used to approximate nonlinear maps under weak assumptions on the structure and properties of the maps. We present deep neural networks using dense and convolutional layers to solve an inverse problem, where we seek to estimate parameters in a FitzHugh-Nagumo model, which consists of a nonlinear system of ordinary differential equations (ODEs). We employ the neural networks to approximate reconstruction maps for model parameter estimation from observational data, where the data comes from the solution of the ODE and takes the form of a time series representing dynamically spiking membrane potential of a (biological) neuron. We target this dynamical model because of the computational challenges it poses in an inference setting, namely, having a highly nonlinear and nonconvex data misfit term and permitting only weakly informative priors on parameters. These challenges cause traditional optimization to fail and alternative algorithms to exhibit large computational costs. We quantify the predictability of model parameters obtained from the neural networks with statistical metrics and investigate the effects of network architectures and presence of noise in observational data. Our results demonstrate that deep neural networks are capable of very accurately estimating parameters in dynamical models from observational data.