Statistical treatment of convolutional neural network super-resolution of inland surface wind for subgrid-scale variability quantification

Machine learning models are frequently employed to perform either purely physics-free or hybrid downscaling of climate data. However, the majority of these implementations operate over relatively small downscaling factors of about 4--6x. This study examines the ability of convolutional neural networks (CNN) to downscale surface wind speed data from three different coarse resolutions (25km, 48km, and 100km side-length grid cells) to 3km and additionally focuses on the ability to recover subgrid-scale variability. Within each downscaling factor, namely 8x, 16x, and 32x, we consider models that produce fine-scale wind speed predictions as functions of different input features: coarse wind fields only; coarse wind and fine-scale topography; and coarse wind, topography, and temporal information in the form of a timestamp. Furthermore, we train one model at 25km to 3km resolution whose fine-scale outputs are probability density function parameters through which sample wind speeds can be generated. All CNN predictions performed on one out-of-sample data outperform classical interpolation. Models with coarse wind and fine topography are shown to exhibit the best performance compared to other models operating across the same downscaling factor. Our timestamp encoding results in lower out-of-sample generalizability compared to other input configurations. Overall, the downscaling factor plays the largest role in model performance.

Neural Networks for Parameter Estimation in Intractable Models

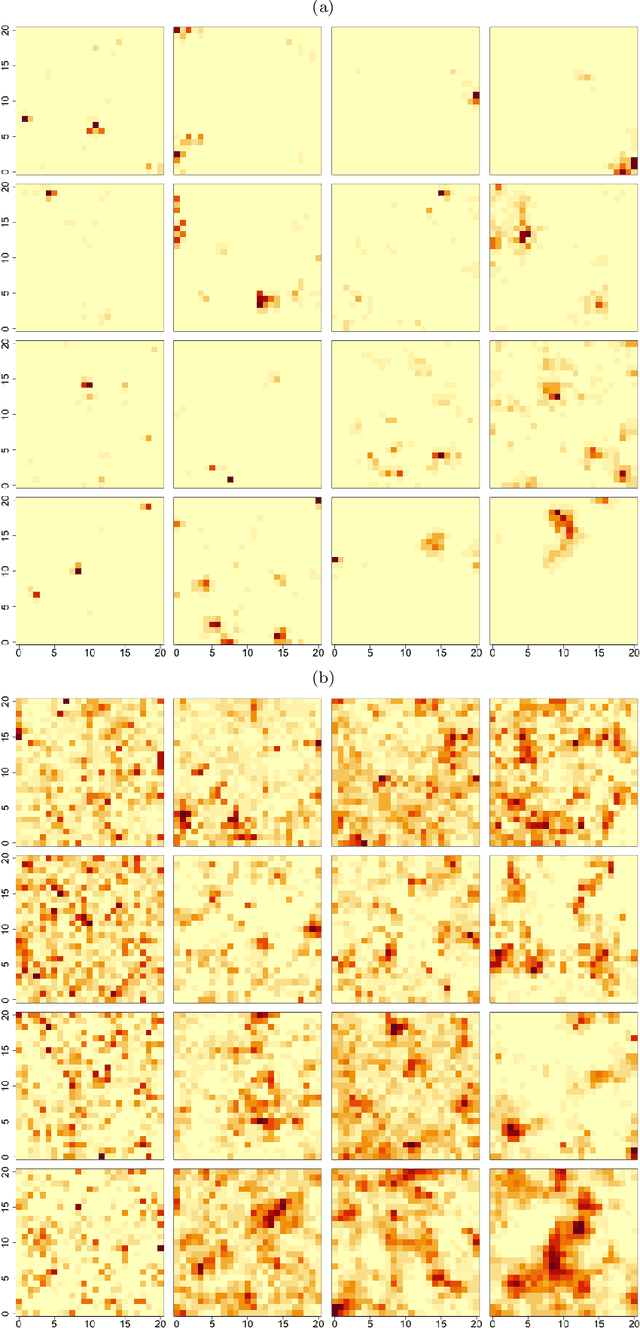
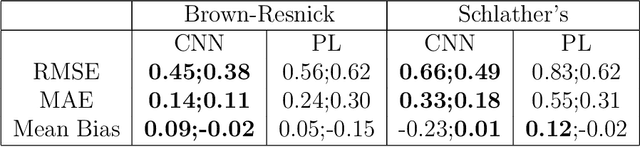
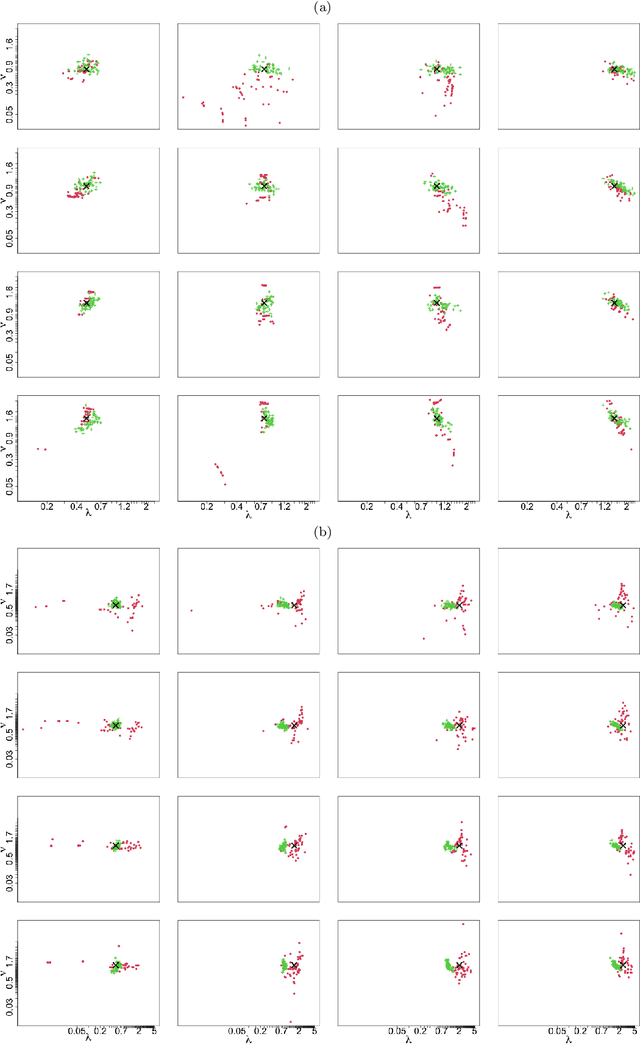
We propose to use deep learning to estimate parameters in statistical models when standard likelihood estimation methods are computationally infeasible. We show how to estimate parameters from max-stable processes, where inference is exceptionally challenging even with small datasets but simulation is straightforward. We use data from model simulations as input and train deep neural networks to learn statistical parameters. Our neural-network-based method provides a competitive alternative to current approaches, as demonstrated by considerable accuracy and computational time improvements. It serves as a proof of concept for deep learning in statistical parameter estimation and can be extended to other estimation problems.

Parameter Estimation with Dense and Convolutional Neural Networks Applied to the FitzHugh-Nagumo ODE

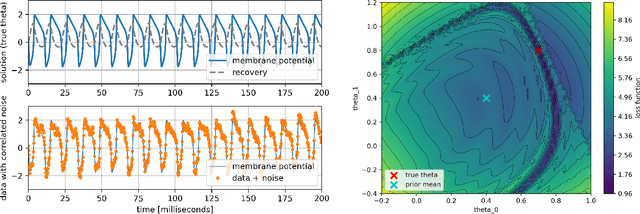
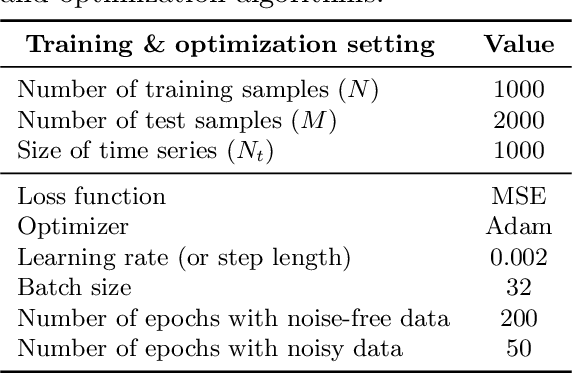
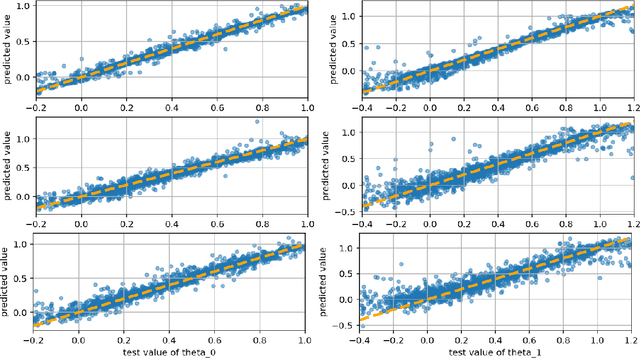
Machine learning algorithms have been successfully used to approximate nonlinear maps under weak assumptions on the structure and properties of the maps. We present deep neural networks using dense and convolutional layers to solve an inverse problem, where we seek to estimate parameters in a FitzHugh-Nagumo model, which consists of a nonlinear system of ordinary differential equations (ODEs). We employ the neural networks to approximate reconstruction maps for model parameter estimation from observational data, where the data comes from the solution of the ODE and takes the form of a time series representing dynamically spiking membrane potential of a (biological) neuron. We target this dynamical model because of the computational challenges it poses in an inference setting, namely, having a highly nonlinear and nonconvex data misfit term and permitting only weakly informative priors on parameters. These challenges cause traditional optimization to fail and alternative algorithms to exhibit large computational costs. We quantify the predictability of model parameters obtained from the neural networks with statistical metrics and investigate the effects of network architectures and presence of noise in observational data. Our results demonstrate that deep neural networks are capable of very accurately estimating parameters in dynamical models from observational data.