Parameter Estimation with Dense and Convolutional Neural Networks Applied to the FitzHugh-Nagumo ODE

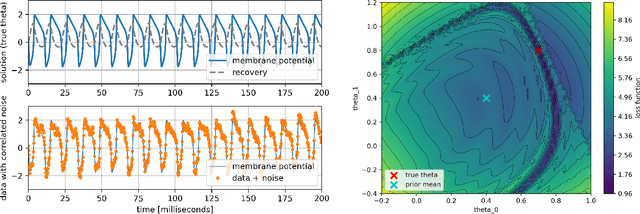
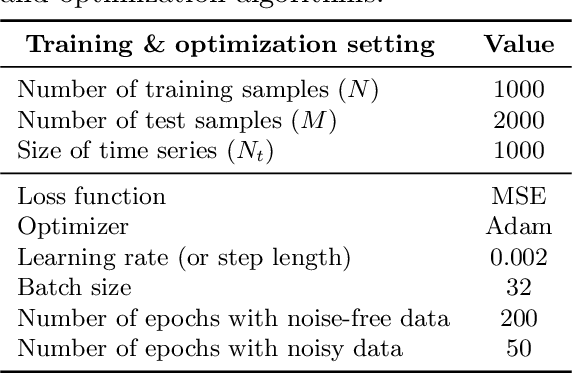
Machine learning algorithms have been successfully used to approximate nonlinear maps under weak assumptions on the structure and properties of the maps. We present deep neural networks using dense and convolutional layers to solve an inverse problem, where we seek to estimate parameters in a FitzHugh-Nagumo model, which consists of a nonlinear system of ordinary differential equations (ODEs). We employ the neural networks to approximate reconstruction maps for model parameter estimation from observational data, where the data comes from the solution of the ODE and takes the form of a time series representing dynamically spiking membrane potential of a (biological) neuron. We target this dynamical model because of the computational challenges it poses in an inference setting, namely, having a highly nonlinear and nonconvex data misfit term and permitting only weakly informative priors on parameters. These challenges cause traditional optimization to fail and alternative algorithms to exhibit large computational costs. We quantify the predictability of model parameters obtained from the neural networks with statistical metrics and investigate the effects of network architectures and presence of noise in observational data. Our results demonstrate that deep neural networks are capable of very accurately estimating parameters in dynamical models from observational data.