Multidimensional Deconvolution with Profiling

In many experimental contexts, it is necessary to statistically remove the impact of instrumental effects in order to physically interpret measurements. This task has been extensively studied in particle physics, where the deconvolution task is called unfolding. A number of recent methods have shown how to perform high-dimensional, unbinned unfolding using machine learning. However, one of the assumptions in all of these methods is that the detector response is accurately modeled in the Monte Carlo simulation. In practice, the detector response depends on a number of nuisance parameters that can be constrained with data. We propose a new algorithm called Profile OmniFold (POF), which works in a similar iterative manner as the OmniFold (OF) algorithm while being able to simultaneously profile the nuisance parameters. We illustrate the method with a Gaussian example as a proof of concept highlighting its promising capabilities.

Toward Model-Agnostic Detection of New Physics Using Data-Driven Signal Regions

In the search for new particles in high-energy physics, it is crucial to select the Signal Region (SR) in such a way that it is enriched with signal events if they are present. While most existing search methods set the region relying on prior domain knowledge, it may be unavailable for a completely novel particle that falls outside the current scope of understanding. We address this issue by proposing a method built upon a model-agnostic but often realistic assumption about the localized topology of the signal events, in which they are concentrated in a certain area of the feature space. Considering the signal component as a localized high-frequency feature, our approach employs the notion of a low-pass filter. We define the SR as an area which is most affected when the observed events are smeared with additive random noise. We overcome challenges in density estimation in the high-dimensional feature space by learning the density ratio of events that potentially include a signal to the complementary observation of events that closely resemble the target events but are free of any signals. By applying our method to simulated $\mathrm{HH} \rightarrow 4b$ events, we demonstrate that the method can efficiently identify a data-driven SR in a high-dimensional feature space in which a high portion of signal events concentrate.

Robust semi-parametric signal detection in particle physics with classifiers decorrelated via optimal transport

Searches of new signals in particle physics are usually done by training a supervised classifier to separate a signal model from the known Standard Model physics (also called the background model). However, even when the signal model is correct, systematic errors in the background model can influence supervised classifiers and might adversely affect the signal detection procedure. To tackle this problem, one approach is to use the (possibly misspecified) classifier only to perform a preliminary signal-enrichment step and then to carry out a bump hunt on the signal-rich sample using only the real experimental data. For this procedure to work, we need a classifier constrained to be decorrelated with one or more protected variables used for the signal detection step. We do this by considering an optimal transport map of the classifier output that makes it independent of the protected variable(s) for the background. We then fit a semi-parametric mixture model to the distribution of the protected variable after making cuts on the transformed classifier to detect the presence of a signal. We compare and contrast this decorrelation method with previous approaches, show that the decorrelation procedure is robust to moderate background misspecification, and analyse the power of the signal detection test as a function of the cut on the classifier.

Neural Likelihood Surfaces for Spatial Processes with Computationally Intensive or Intractable Likelihoods

In spatial statistics, fast and accurate parameter estimation coupled with a reliable means of uncertainty quantification can be a challenging task when fitting a spatial process to real-world data because the likelihood function might be slow to evaluate or intractable. In this work, we propose using convolutional neural networks (CNNs) to learn the likelihood function of a spatial process. Through a specifically designed classification task, our neural network implicitly learns the likelihood function, even in situations where the exact likelihood is not explicitly available. Once trained on the classification task, our neural network is calibrated using Platt scaling which improves the accuracy of the neural likelihood surfaces. To demonstrate our approach, we compare maximum likelihood estimates and approximate confidence regions constructed from the neural likelihood surface with the equivalent for exact or approximate likelihood for two different spatial processes: a Gaussian Process, which has a computationally intensive likelihood function for large datasets, and a Brown-Resnick Process, which has an intractable likelihood function. We also compare the neural likelihood surfaces to the exact and approximate likelihood surfaces for the Gaussian Process and Brown-Resnick Process, respectively. We conclude that our method provides fast and accurate parameter estimation with a reliable method of uncertainty quantification in situations where standard methods are either undesirably slow or inaccurate.

Simulation-Based Inference with WALDO: Perfectly Calibrated Confidence Regions Using Any Prediction or Posterior Estimation Algorithm

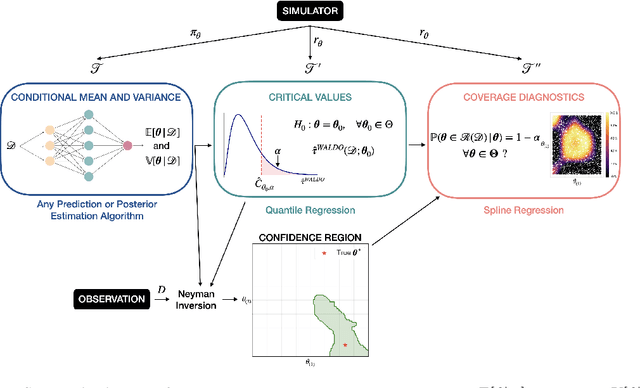
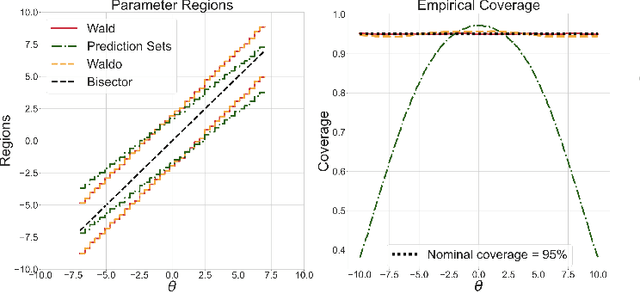
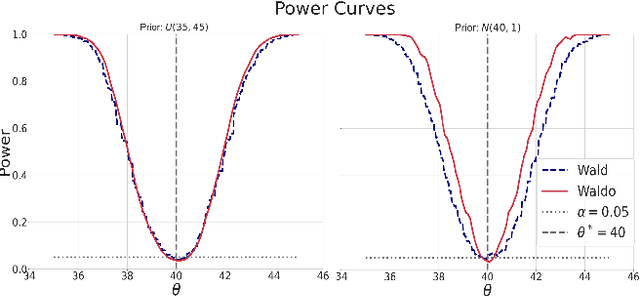
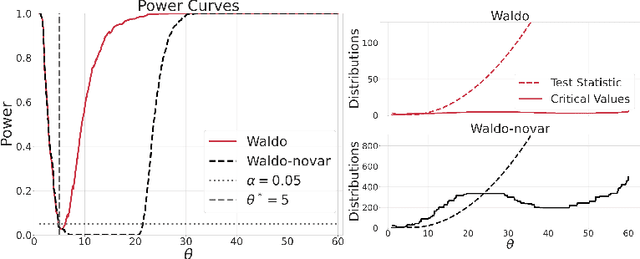
The vast majority of modern machine learning targets prediction problems, with algorithms such as Deep Neural Networks revolutionizing the accuracy of point predictions for high-dimensional complex data. Predictive approaches are now used in many domain sciences to directly estimate internal parameters of interest in theoretical simulator-based models. In parallel, common alternatives focus on estimating the full posterior using modern neural density estimators such as normalizing flows. However, an open problem in simulation-based inference (SBI) is how to construct properly calibrated confidence regions for internal parameters with nominal conditional coverage and high power. Many SBI methods are indeed known to produce overly confident posterior approximations, yielding misleading uncertainty estimates. Similarly, existing approaches for uncertainty quantification in deep learning provide no guarantees on conditional coverage. In this work, we present WALDO, a novel method for constructing correctly calibrated confidence regions in SBI. WALDO reframes the well-known Wald test and uses Neyman inversion to convert point predictions and posteriors from any prediction or posterior estimation algorithm to confidence sets with correct conditional coverage, even for finite sample sizes. As a concrete example, we demonstrate how a recently proposed deep learning prediction approach for particle energies in high-energy physics can be recalibrated using WALDO to produce confidence intervals with correct coverage and high power.

Semi-Supervised Anomaly Detection - Towards Model-Independent Searches of New Physics

Most classification algorithms used in high energy physics fall under the category of supervised machine learning. Such methods require a training set containing both signal and background events and are prone to classification errors should this training data be systematically inaccurate for example due to the assumed MC model. To complement such model-dependent searches, we propose an algorithm based on semi-supervised anomaly detection techniques, which does not require a MC training sample for the signal data. We first model the background using a multivariate Gaussian mixture model. We then search for deviations from this model by fitting to the observations a mixture of the background model and a number of additional Gaussians. This allows us to perform pattern recognition of any anomalous excess over the background. We show by a comparison to neural network classifiers that such an approach is a lot more robust against misspecification of the signal MC than supervised classification. In cases where there is an unexpected signal, a neural network might fail to correctly identify it, while anomaly detection does not suffer from such a limitation. On the other hand, when there are no systematic errors in the training data, both methods perform comparably.