Statistical Inference for Optimal Transport Maps: Recent Advances and Perspectives

In many applications of optimal transport (OT), the object of primary interest is the optimal transport map. This map rearranges mass from one probability distribution to another in the most efficient way possible by minimizing a specified cost. In this paper we review recent advances in estimating and developing limit theorems for the OT map, using samples from the underlying distributions. We also review parallel lines of work that establish similar results for special cases and variants of the basic OT setup. We conclude with a discussion of key directions for future research with the goal of providing practitioners with reliable inferential tools.

Assumption-Lean Post-Integrated Inference with Negative Control Outcomes

Data integration has become increasingly common in aligning multiple heterogeneous datasets. With high-dimensional outcomes, data integration methods aim to extract low-dimensional embeddings of observations to remove unwanted variations, such as batch effects and unmeasured covariates, inherent in data collected from different sources. However, multiple hypothesis testing after data integration can be substantially biased due to the data-dependent integration processes. To address this challenge, we introduce a robust post-integrated inference (PII) method that adjusts for latent heterogeneity using negative control outcomes. By leveraging causal interpretations, we derive nonparametric identification conditions that form the basis of our PII approach. Our assumption-lean semiparametric inference method extends robustness and generality to projected direct effect estimands that account for mediators, confounders, and moderators. These estimands remain statistically meaningful under model misspecifications and with error-prone embeddings. We provide deterministic quantifications of the bias of target estimands induced by estimated embeddings and finite-sample linear expansions of the estimators with uniform concentration bounds on the residuals for all outcomes. The proposed doubly robust estimators are consistent and efficient under minimal assumptions, facilitating data-adaptive estimation with machine learning algorithms. Using random forests, we evaluate empirical statistical errors in simulations and analyze single-cell CRISPR perturbed datasets with potential unmeasured confounders.

Multidimensional Deconvolution with Profiling

In many experimental contexts, it is necessary to statistically remove the impact of instrumental effects in order to physically interpret measurements. This task has been extensively studied in particle physics, where the deconvolution task is called unfolding. A number of recent methods have shown how to perform high-dimensional, unbinned unfolding using machine learning. However, one of the assumptions in all of these methods is that the detector response is accurately modeled in the Monte Carlo simulation. In practice, the detector response depends on a number of nuisance parameters that can be constrained with data. We propose a new algorithm called Profile OmniFold (POF), which works in a similar iterative manner as the OmniFold (OF) algorithm while being able to simultaneously profile the nuisance parameters. We illustrate the method with a Gaussian example as a proof of concept highlighting its promising capabilities.

Robust semi-parametric signal detection in particle physics with classifiers decorrelated via optimal transport

Searches of new signals in particle physics are usually done by training a supervised classifier to separate a signal model from the known Standard Model physics (also called the background model). However, even when the signal model is correct, systematic errors in the background model can influence supervised classifiers and might adversely affect the signal detection procedure. To tackle this problem, one approach is to use the (possibly misspecified) classifier only to perform a preliminary signal-enrichment step and then to carry out a bump hunt on the signal-rich sample using only the real experimental data. For this procedure to work, we need a classifier constrained to be decorrelated with one or more protected variables used for the signal detection step. We do this by considering an optimal transport map of the classifier output that makes it independent of the protected variable(s) for the background. We then fit a semi-parametric mixture model to the distribution of the protected variable after making cuts on the transformed classifier to detect the presence of a signal. We compare and contrast this decorrelation method with previous approaches, show that the decorrelation procedure is robust to moderate background misspecification, and analyse the power of the signal detection test as a function of the cut on the classifier.

Causal Inference for Genomic Data with Multiple Heterogeneous Outcomes

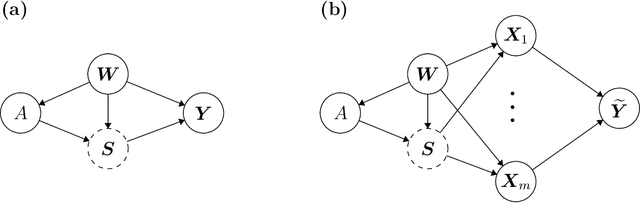
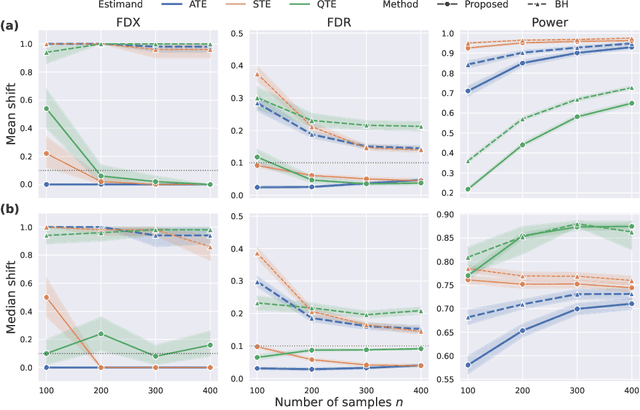
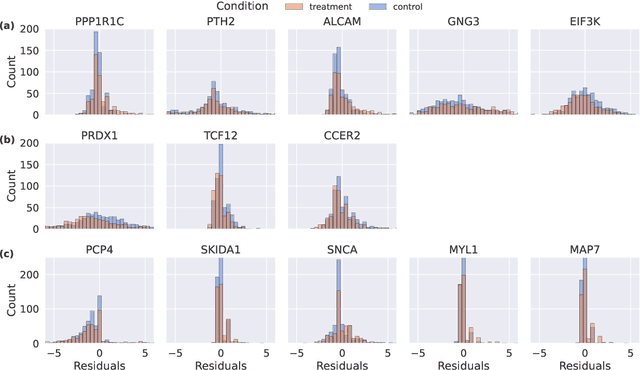
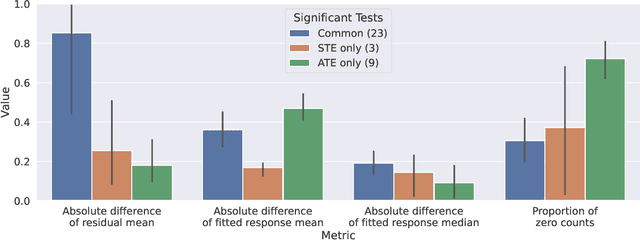
With the evolution of single-cell RNA sequencing techniques into a standard approach in genomics, it has become possible to conduct cohort-level causal inferences based on single-cell-level measurements. However, the individual gene expression levels of interest are not directly observable; instead, only repeated proxy measurements from each individual's cells are available, providing a derived outcome to estimate the underlying outcome for each of many genes. In this paper, we propose a generic semiparametric inference framework for doubly robust estimation with multiple derived outcomes, which also encompasses the usual setting of multiple outcomes when the response of each unit is available. To reliably quantify the causal effects of heterogeneous outcomes, we specialize the analysis to the standardized average treatment effects and the quantile treatment effects. Through this, we demonstrate the use of the semiparametric inferential results for doubly robust estimators derived from both Von Mises expansions and estimating equations. A multiple testing procedure based on the Gaussian multiplier bootstrap is tailored for doubly robust estimators to control the false discovery exceedance rate. Applications in single-cell CRISPR perturbation analysis and individual-level differential expression analysis demonstrate the utility of the proposed methods and offer insights into the usage of different estimands for causal inference in genomics.

Double Cross-fit Doubly Robust Estimators: Beyond Series Regression

Doubly robust estimators with cross-fitting have gained popularity in causal inference due to their favorable structure-agnostic error guarantees. However, when additional structure, such as H\"{o}lder smoothness, is available then more accurate "double cross-fit doubly robust" (DCDR) estimators can be constructed by splitting the training data and undersmoothing nuisance function estimators on independent samples. We study a DCDR estimator of the Expected Conditional Covariance, a functional of interest in causal inference and conditional independence testing, and derive a series of increasingly powerful results with progressively stronger assumptions. We first provide a structure-agnostic error analysis for the DCDR estimator with no assumptions on the nuisance functions or their estimators. Then, assuming the nuisance functions are H\"{o}lder smooth, but without assuming knowledge of the true smoothness level or the covariate density, we establish that DCDR estimators with several linear smoothers are semiparametric efficient under minimal conditions and achieve fast convergence rates in the non-$\sqrt{n}$ regime. When the covariate density and smoothnesses are known, we propose a minimax rate-optimal DCDR estimator based on undersmoothed kernel regression. Moreover, we show an undersmoothed DCDR estimator satisfies a slower-than-$\sqrt{n}$ central limit theorem, and that inference is possible even in the non-$\sqrt{n}$ regime. Finally, we support our theoretical results with simulations, providing intuition for double cross-fitting and undersmoothing, demonstrating where our estimator achieves semiparametric efficiency while the usual "single cross-fit" estimator fails, and illustrating asymptotic normality for the undersmoothed DCDR estimator.

Semi-Supervised U-statistics

Semi-supervised datasets are ubiquitous across diverse domains where obtaining fully labeled data is costly or time-consuming. The prevalence of such datasets has consistently driven the demand for new tools and methods that exploit the potential of unlabeled data. Responding to this demand, we introduce semi-supervised U-statistics enhanced by the abundance of unlabeled data, and investigate their statistical properties. We show that the proposed approach is asymptotically Normal and exhibits notable efficiency gains over classical U-statistics by effectively integrating various powerful prediction tools into the framework. To understand the fundamental difficulty of the problem, we derive minimax lower bounds in semi-supervised settings and showcase that our procedure is semi-parametrically efficient under regularity conditions. Moreover, tailored to bivariate kernels, we propose a refined approach that outperforms the classical U-statistic across all degeneracy regimes, and demonstrate its optimality properties. Simulation studies are conducted to corroborate our findings and to further demonstrate our framework.

Simultaneous inference for generalized linear models with unmeasured confounders

Tens of thousands of simultaneous hypothesis tests are routinely performed in genomic studies to identify differentially expressed genes. However, due to unmeasured confounders, many standard statistical approaches may be substantially biased. This paper investigates the large-scale hypothesis testing problem for multivariate generalized linear models in the presence of confounding effects. Under arbitrary confounding mechanisms, we propose a unified statistical estimation and inference framework that harnesses orthogonal structures and integrates linear projections into three key stages. It begins by disentangling marginal and uncorrelated confounding effects to recover the latent coefficients. Subsequently, latent factors and primary effects are jointly estimated through lasso-type optimization. Finally, we incorporate projected and weighted bias-correction steps for hypothesis testing. Theoretically, we establish the identification conditions of various effects and non-asymptotic error bounds. We show effective Type-I error control of asymptotic $z$-tests as sample and response sizes approach infinity. Numerical experiments demonstrate that the proposed method controls the false discovery rate by the Benjamini-Hochberg procedure and is more powerful than alternative methods. By comparing single-cell RNA-seq counts from two groups of samples, we demonstrate the suitability of adjusting confounding effects when significant covariates are absent from the model.

The Fundamental Limits of Structure-Agnostic Functional Estimation

Many recent developments in causal inference, and functional estimation problems more generally, have been motivated by the fact that classical one-step (first-order) debiasing methods, or their more recent sample-split double machine-learning avatars, can outperform plugin estimators under surprisingly weak conditions. These first-order corrections improve on plugin estimators in a black-box fashion, and consequently are often used in conjunction with powerful off-the-shelf estimation methods. These first-order methods are however provably suboptimal in a minimax sense for functional estimation when the nuisance functions live in Holder-type function spaces. This suboptimality of first-order debiasing has motivated the development of "higher-order" debiasing methods. The resulting estimators are, in some cases, provably optimal over Holder-type spaces, but both the estimators which are minimax-optimal and their analyses are crucially tied to properties of the underlying function space. In this paper we investigate the fundamental limits of structure-agnostic functional estimation, where relatively weak conditions are placed on the underlying nuisance functions. We show that there is a strong sense in which existing first-order methods are optimal. We achieve this goal by providing a formalization of the problem of functional estimation with black-box nuisance function estimates, and deriving minimax lower bounds for this problem. Our results highlight some clear tradeoffs in functional estimation -- if we wish to remain agnostic to the underlying nuisance function spaces, impose only high-level rate conditions, and maintain compatibility with black-box nuisance estimators then first-order methods are optimal. When we have an understanding of the structure of the underlying nuisance functions then carefully constructed higher-order estimators can outperform first-order estimators.

Feature Importance: A Closer Look at Shapley Values and LOCO

There is much interest lately in explainability in statistics and machine learning. One aspect of explainability is to quantify the importance of various features (or covariates). Two popular methods for defining variable importance are LOCO (Leave Out COvariates) and Shapley Values. We take a look at the properties of these methods and their advantages and disadvantages. We are particularly interested in the effect of correlation between features which can obscure interpretability. Contrary to some claims, Shapley values do not eliminate feature correlation. We critique the game theoretic axioms for Shapley values and suggest some new axioms. We propose new, more statistically oriented axioms for feature importance and some measures that satisfy these axioms. However, correcting for correlation is a Faustian bargain: removing the effect of correlation creates other forms of bias. Ultimately, we recommend a slightly modified version of LOCO. We briefly consider how to modify Shapley values to better address feature correlation.