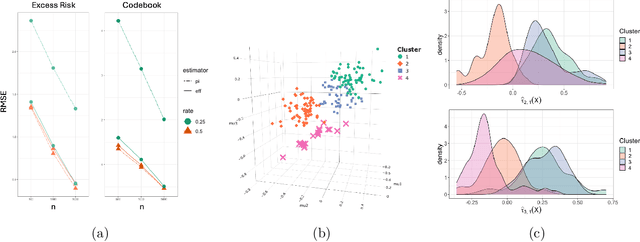
Hierarchical and Density-based Causal Clustering

Understanding treatment effect heterogeneity is vital for scientific and policy research. However, identifying and evaluating heterogeneous treatment effects pose significant challenges due to the typically unknown subgroup structure. Recently, a novel approach, causal k-means clustering, has emerged to assess heterogeneity of treatment effect by applying the k-means algorithm to unknown counterfactual regression functions. In this paper, we expand upon this framework by integrating hierarchical and density-based clustering algorithms. We propose plug-in estimators that are simple and readily implementable using off-the-shelf algorithms. Unlike k-means clustering, which requires the margin condition, our proposed estimators do not rely on strong structural assumptions on the outcome process. We go on to study their rate of convergence, and show that under the minimal regularity conditions, the additional cost of causal clustering is essentially the estimation error of the outcome regression functions. Our findings significantly extend the capabilities of the causal clustering framework, thereby contributing to the progression of methodologies for identifying homogeneous subgroups in treatment response, consequently facilitating more nuanced and targeted interventions. The proposed methods also open up new avenues for clustering with generic pseudo-outcomes. We explore finite sample properties via simulation, and illustrate the proposed methods in voting and employment projection datasets.

Causal K-Means Clustering

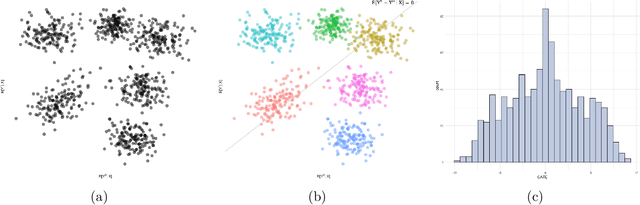
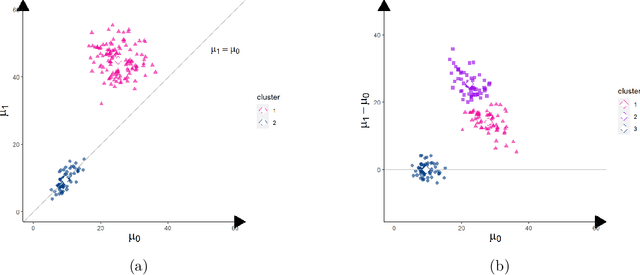
Causal effects are often characterized with population summaries. These might provide an incomplete picture when there are heterogeneous treatment effects across subgroups. Since the subgroup structure is typically unknown, it is more challenging to identify and evaluate subgroup effects than population effects. We propose a new solution to this problem: Causal k-Means Clustering, which harnesses the widely-used k-means clustering algorithm to uncover the unknown subgroup structure. Our problem differs significantly from the conventional clustering setup since the variables to be clustered are unknown counterfactual functions. We present a plug-in estimator which is simple and readily implementable using off-the-shelf algorithms, and study its rate of convergence. We also develop a new bias-corrected estimator based on nonparametric efficiency theory and double machine learning, and show that this estimator achieves fast root-n rates and asymptotic normality in large nonparametric models. Our proposed methods are especially useful for modern outcome-wide studies with multiple treatment levels. Further, our framework is extensible to clustering with generic pseudo-outcomes, such as partially observed outcomes or otherwise unknown functions. Finally, we explore finite sample properties via simulation, and illustrate the proposed methods in a study of treatment programs for adolescent substance abuse.

Causal Inference for Genomic Data with Multiple Heterogeneous Outcomes

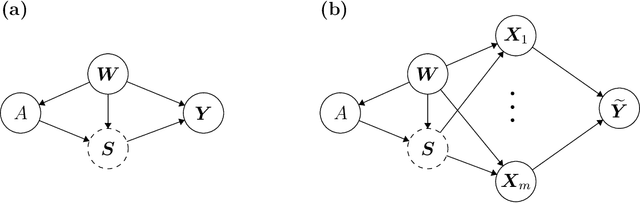
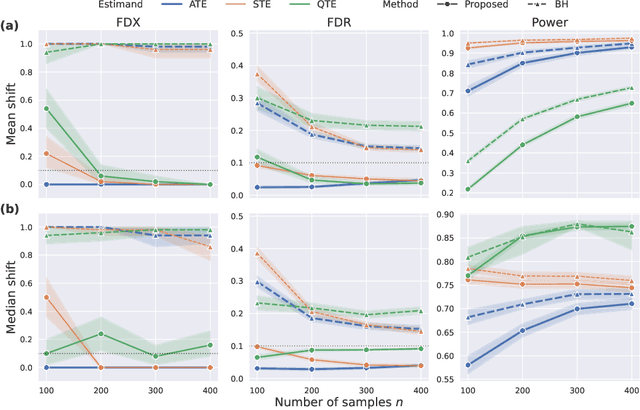
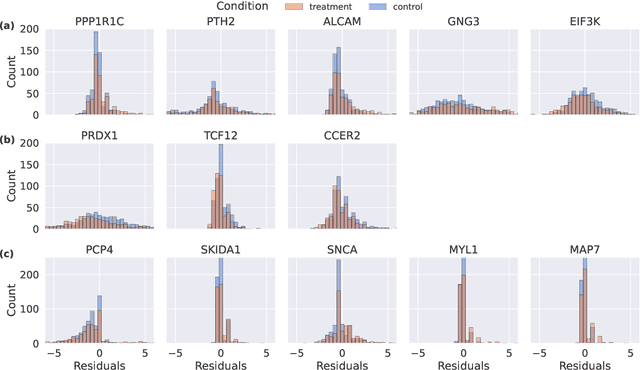
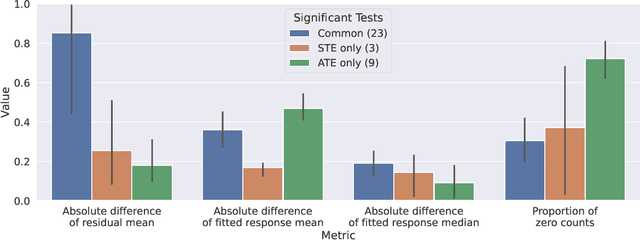
With the evolution of single-cell RNA sequencing techniques into a standard approach in genomics, it has become possible to conduct cohort-level causal inferences based on single-cell-level measurements. However, the individual gene expression levels of interest are not directly observable; instead, only repeated proxy measurements from each individual's cells are available, providing a derived outcome to estimate the underlying outcome for each of many genes. In this paper, we propose a generic semiparametric inference framework for doubly robust estimation with multiple derived outcomes, which also encompasses the usual setting of multiple outcomes when the response of each unit is available. To reliably quantify the causal effects of heterogeneous outcomes, we specialize the analysis to the standardized average treatment effects and the quantile treatment effects. Through this, we demonstrate the use of the semiparametric inferential results for doubly robust estimators derived from both Von Mises expansions and estimating equations. A multiple testing procedure based on the Gaussian multiplier bootstrap is tailored for doubly robust estimators to control the false discovery exceedance rate. Applications in single-cell CRISPR perturbation analysis and individual-level differential expression analysis demonstrate the utility of the proposed methods and offer insights into the usage of different estimands for causal inference in genomics.

Double Cross-fit Doubly Robust Estimators: Beyond Series Regression

Doubly robust estimators with cross-fitting have gained popularity in causal inference due to their favorable structure-agnostic error guarantees. However, when additional structure, such as H\"{o}lder smoothness, is available then more accurate "double cross-fit doubly robust" (DCDR) estimators can be constructed by splitting the training data and undersmoothing nuisance function estimators on independent samples. We study a DCDR estimator of the Expected Conditional Covariance, a functional of interest in causal inference and conditional independence testing, and derive a series of increasingly powerful results with progressively stronger assumptions. We first provide a structure-agnostic error analysis for the DCDR estimator with no assumptions on the nuisance functions or their estimators. Then, assuming the nuisance functions are H\"{o}lder smooth, but without assuming knowledge of the true smoothness level or the covariate density, we establish that DCDR estimators with several linear smoothers are semiparametric efficient under minimal conditions and achieve fast convergence rates in the non-$\sqrt{n}$ regime. When the covariate density and smoothnesses are known, we propose a minimax rate-optimal DCDR estimator based on undersmoothed kernel regression. Moreover, we show an undersmoothed DCDR estimator satisfies a slower-than-$\sqrt{n}$ central limit theorem, and that inference is possible even in the non-$\sqrt{n}$ regime. Finally, we support our theoretical results with simulations, providing intuition for double cross-fitting and undersmoothing, demonstrating where our estimator achieves semiparametric efficiency while the usual "single cross-fit" estimator fails, and illustrating asymptotic normality for the undersmoothed DCDR estimator.

Continuous Treatment Effects with Surrogate Outcomes

In many real-world causal inference applications, the primary outcomes (labels) are often partially missing, especially if they are expensive or difficult to collect. If the missingness depends on covariates (i.e., missingness is not completely at random), analyses based on fully-observed samples alone may be biased. Incorporating surrogates, which are fully observed post-treatment variables related to the primary outcome, can improve estimation in this case. In this paper, we study the role of surrogates in estimating continuous treatment effects and propose a doubly robust method to efficiently incorporate surrogates in the analysis, which uses both labeled and unlabeled data and does not suffer from the above selection bias problem. Importantly, we establish asymptotic normality of the proposed estimator and show possible improvements on the variance compared with methods that solely use labeled data. Extensive simulations show our methods enjoy appealing empirical performance.

The Fundamental Limits of Structure-Agnostic Functional Estimation

Many recent developments in causal inference, and functional estimation problems more generally, have been motivated by the fact that classical one-step (first-order) debiasing methods, or their more recent sample-split double machine-learning avatars, can outperform plugin estimators under surprisingly weak conditions. These first-order corrections improve on plugin estimators in a black-box fashion, and consequently are often used in conjunction with powerful off-the-shelf estimation methods. These first-order methods are however provably suboptimal in a minimax sense for functional estimation when the nuisance functions live in Holder-type function spaces. This suboptimality of first-order debiasing has motivated the development of "higher-order" debiasing methods. The resulting estimators are, in some cases, provably optimal over Holder-type spaces, but both the estimators which are minimax-optimal and their analyses are crucially tied to properties of the underlying function space. In this paper we investigate the fundamental limits of structure-agnostic functional estimation, where relatively weak conditions are placed on the underlying nuisance functions. We show that there is a strong sense in which existing first-order methods are optimal. We achieve this goal by providing a formalization of the problem of functional estimation with black-box nuisance function estimates, and deriving minimax lower bounds for this problem. Our results highlight some clear tradeoffs in functional estimation -- if we wish to remain agnostic to the underlying nuisance function spaces, impose only high-level rate conditions, and maintain compatibility with black-box nuisance estimators then first-order methods are optimal. When we have an understanding of the structure of the underlying nuisance functions then carefully constructed higher-order estimators can outperform first-order estimators.

An Efficient Doubly-Robust Test for the Kernel Treatment Effect

The average treatment effect, which is the difference in expectation of the counterfactuals, is probably the most popular target effect in causal inference with binary treatments. However, treatments may have effects beyond the mean, for instance decreasing or increasing the variance. We propose a new kernel-based test for distributional effects of the treatment. It is, to the best of our knowledge, the first kernel-based, doubly-robust test with provably valid type-I error. Furthermore, our proposed algorithm is efficient, avoiding the use of permutations.

Doubly Robust Counterfactual Classification

We study counterfactual classification as a new tool for decision-making under hypothetical (contrary to fact) scenarios. We propose a doubly-robust nonparametric estimator for a general counterfactual classifier, where we can incorporate flexible constraints by casting the classification problem as a nonlinear mathematical program involving counterfactuals. We go on to analyze the rates of convergence of the estimator and provide a closed-form expression for its asymptotic distribution. Our analysis shows that the proposed estimator is robust against nuisance model misspecification, and can attain fast $\sqrt{n}$ rates with tractable inference even when using nonparametric machine learning approaches. We study the empirical performance of our methods by simulation and apply them for recidivism risk prediction.

The role of the geometric mean in case-control studies

Historically used in settings where the outcome is rare or data collection is expensive, outcome-dependent sampling is relevant to many modern settings where data is readily available for a biased sample of the target population, such as public administrative data. Under outcome-dependent sampling, common effect measures such as the average risk difference and the average risk ratio are not identified, but the conditional odds ratio is. Aggregation of the conditional odds ratio is challenging since summary measures are generally not identified. Furthermore, the marginal odds ratio can be larger (or smaller) than all conditional odds ratios. This so-called non-collapsibility of the odds ratio is avoidable if we use an alternative aggregation to the standard arithmetic mean. We provide a new definition of collapsibility that makes this choice of aggregation method explicit, and we demonstrate that the odds ratio is collapsible under geometric aggregation. We describe how to partially identify, estimate, and do inference on the geometric odds ratio under outcome-dependent sampling. Our proposed estimator is based on the efficient influence function and therefore has doubly robust-style properties.

Doubly robust confidence sequences for sequential causal inference

This paper derives time-uniform confidence sequences (CS) for causal effects in experimental and observational settings. A confidence sequence for a target parameter $\psi$ is a sequence of confidence intervals $(C_t)_{t=1}^\infty$ such that every one of these intervals simultaneously captures $\psi$ with high probability. Such CSs provide valid statistical inference for $\psi$ at arbitrary stopping times, unlike classical fixed-time confidence intervals which require the sample size to be fixed in advance. Existing methods for constructing CSs focus on the nonasymptotic regime where certain assumptions (such as known bounds on the random variables) are imposed, while doubly-robust estimators of causal effects rely on (asymptotic) semiparametric theory. We use sequential versions of central limit theorem arguments to construct large-sample CSs for causal estimands, with a particular focus on the average treatment effect (ATE) under nonparametric conditions. These CSs allow analysts to update statistical inferences about the ATE in lieu of new data, and experiments can be continuously monitored, stopped, or continued for any data-dependent reason, all while controlling the type-I error rate. Finally, we describe how these CSs readily extend to other causal estimands and estimators, providing a new framework for sequential causal inference in a wide array of problems.