Scalable kernel balancing weights in a nationwide observational study of hospital profit status and heart attack outcomes

Weighting is a general and often-used method for statistical adjustment. Weighting has two objectives: first, to balance covariate distributions, and second, to ensure that the weights have minimal dispersion and thus produce a more stable estimator. A recent, increasingly common approach directly optimizes the weights toward these two objectives. However, this approach has not yet been feasible in large-scale datasets when investigators wish to flexibly balance general basis functions in an extended feature space. For example, many balancing approaches cannot scale to national-level health services research studies. To address this practical problem, we describe a scalable and flexible approach to weighting that integrates a basis expansion in a reproducing kernel Hilbert space with state-of-the-art convex optimization techniques. Specifically, we use the rank-restricted Nystr\"{o}m method to efficiently compute a kernel basis for balancing in {nearly} linear time and space, and then use the specialized first-order alternating direction method of multipliers to rapidly find the optimal weights. In an extensive simulation study, we provide new insights into the performance of weighting estimators in large datasets, showing that the proposed approach substantially outperforms others in terms of accuracy and speed. Finally, we use this weighting approach to conduct a national study of the relationship between hospital profit status and heart attack outcomes in a comprehensive dataset of 1.27 million patients. We find that for-profit hospitals use interventional cardiology to treat heart attacks at similar rates as other hospitals, but have higher mortality and readmission rates.

Fair and Robust Estimation of Heterogeneous Treatment Effects for Policy Learning

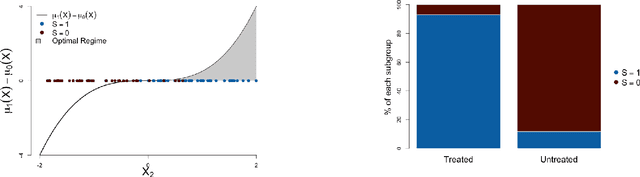
We propose a simple and general framework for nonparametric estimation of heterogeneous treatment effects under fairness constraints. Under standard regularity conditions, we show that the resulting estimators possess the double robustness property. We use this framework to characterize the trade-off between fairness and the maximum welfare achievable by the optimal policy. We evaluate the methods in a simulation study and illustrate them in a real-world case study.

Doubly Robust Counterfactual Classification

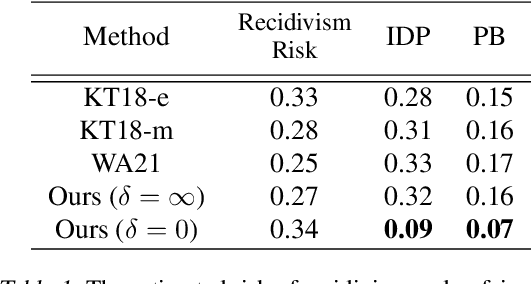
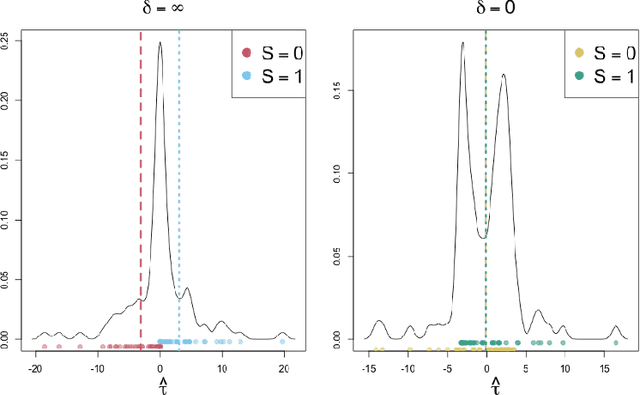
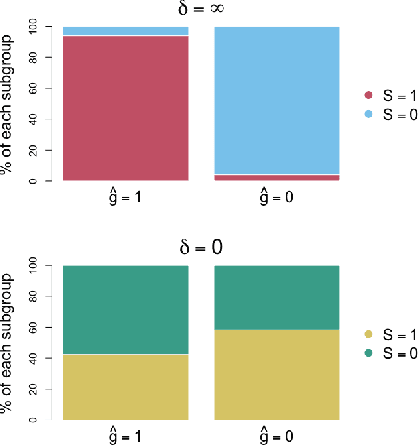
We study counterfactual classification as a new tool for decision-making under hypothetical (contrary to fact) scenarios. We propose a doubly-robust nonparametric estimator for a general counterfactual classifier, where we can incorporate flexible constraints by casting the classification problem as a nonlinear mathematical program involving counterfactuals. We go on to analyze the rates of convergence of the estimator and provide a closed-form expression for its asymptotic distribution. Our analysis shows that the proposed estimator is robust against nuisance model misspecification, and can attain fast $\sqrt{n}$ rates with tractable inference even when using nonparametric machine learning approaches. We study the empirical performance of our methods by simulation and apply them for recidivism risk prediction.