Multi-Armed Sequential Hypothesis Testing by Betting

We consider a variant of sequential testing by betting where, at each time step, the statistician is presented with multiple data sources (arms) and obtains data by choosing one of the arms. We consider the composite global null hypothesis $\mathscr{P}$ that all arms are null in a certain sense (e.g. all dosages of a treatment are ineffective) and we are interested in rejecting $\mathscr{P}$ in favor of a composite alternative $\mathscr{Q}$ where at least one arm is non-null (e.g. there exists an effective treatment dosage). We posit an optimality desideratum that we describe informally as follows: even if several arms are non-null, we seek $e$-processes and sequential tests whose performance are as strong as the ones that have oracle knowledge about which arm generates the most evidence against $\mathscr{P}$. Formally, we generalize notions of log-optimality and expected rejection time optimality to more than one arm, obtaining matching lower and upper bounds for both. A key technical device in this optimality analysis is a modified upper-confidence-bound-like algorithm for unobservable but sufficiently "estimable" rewards. In the design of this algorithm, we derive nonasymptotic concentration inequalities for optimal wealth growth rates in the sense of Kelly [1956]. These may be of independent interest.

On Nonasymptotic Confidence Intervals for Treatment Effects in Randomized Experiments

We study nonasymptotic (finite-sample) confidence intervals for treatment effects in randomized experiments. In the existing literature, the effective sample sizes of nonasymptotic confidence intervals tend to be looser than the corresponding central-limit-theorem-based confidence intervals by a factor depending on the square root of the propensity score. We show that this performance gap can be closed, designing nonasymptotic confidence intervals that have the same effective sample size as their asymptotic counterparts. Our approach involves systematic exploitation of negative dependence or variance adaptivity (or both). We also show that the nonasymptotic rates that we achieve are unimprovable in an information-theoretic sense.

Anytime-valid off-policy inference for contextual bandits

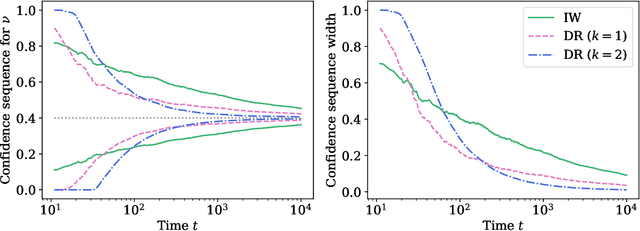
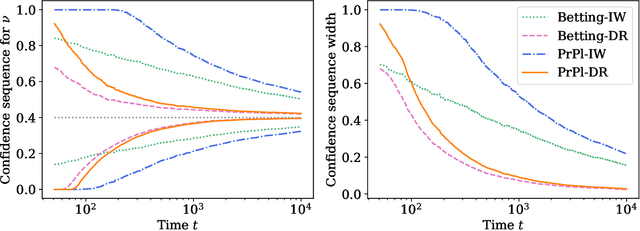
Contextual bandits are a modern staple tool for active sequential experimentation in the tech industry. They involve online learning algorithms that adaptively (over time) learn policies to map observed contexts $X_t$ to actions $A_t$ in an attempt to maximize stochastic rewards $R_t$. This adaptivity raises interesting but hard statistical inference questions, especially counterfactual ones: for example, it is often of interest to estimate the properties of a hypothetical policy that is different from the logging policy that was used to collect the data -- a problem known as "off-policy evaluation" (OPE). Using modern martingale techniques, we present a comprehensive framework for OPE inference that relax many unnecessary assumptions made in past work, significantly improving on them theoretically and empirically. Our methods remain valid in very general settings, and can be employed while the original experiment is still running (that is, not necessarily post-hoc), when the logging policy may be itself changing (due to learning), and even if the context distributions are drifting over time. More concretely, we derive confidence sequences for various functionals of interest in OPE. These include doubly robust ones for time-varying off-policy mean reward values, but also confidence bands for the entire CDF of the off-policy reward distribution. All of our methods (a) are valid at arbitrary stopping times (b) only make nonparametric assumptions, and (c) do not require known bounds on the maximal importance weights, and (d) adapt to the empirical variance of the reward and weight distributions. In summary, our methods enable anytime-valid off-policy inference using adaptively collected contextual bandit data.

Locally private nonparametric confidence intervals and sequences

This work derives methods for performing nonparametric, nonasymptotic statistical inference for population parameters under the constraint of local differential privacy (LDP). Given observations $(X_1, \dots, X_n)$ with mean $\mu^\star$ that are privatized into $(Z_1, \dots, Z_n)$, we introduce confidence intervals (CI) and time-uniform confidence sequences (CS) for $\mu^\star \in \mathbb R$ when only given access to the privatized data. We introduce a nonparametric and sequentially interactive generalization of Warner's famous "randomized response" mechanism, satisfying LDP for arbitrary bounded random variables, and then provide CIs and CSs for their means given access to the resulting privatized observations. We extend these CSs to capture time-varying (non-stationary) means, and conclude by illustrating how these methods can be used to conduct private online A/B tests.

Doubly robust confidence sequences for sequential causal inference

This paper derives time-uniform confidence sequences (CS) for causal effects in experimental and observational settings. A confidence sequence for a target parameter $\psi$ is a sequence of confidence intervals $(C_t)_{t=1}^\infty$ such that every one of these intervals simultaneously captures $\psi$ with high probability. Such CSs provide valid statistical inference for $\psi$ at arbitrary stopping times, unlike classical fixed-time confidence intervals which require the sample size to be fixed in advance. Existing methods for constructing CSs focus on the nonasymptotic regime where certain assumptions (such as known bounds on the random variables) are imposed, while doubly-robust estimators of causal effects rely on (asymptotic) semiparametric theory. We use sequential versions of central limit theorem arguments to construct large-sample CSs for causal estimands, with a particular focus on the average treatment effect (ATE) under nonparametric conditions. These CSs allow analysts to update statistical inferences about the ATE in lieu of new data, and experiments can be continuously monitored, stopped, or continued for any data-dependent reason, all while controlling the type-I error rate. Finally, we describe how these CSs readily extend to other causal estimands and estimators, providing a new framework for sequential causal inference in a wide array of problems.

Variance-adaptive confidence sequences by betting

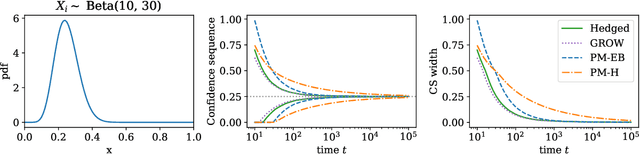
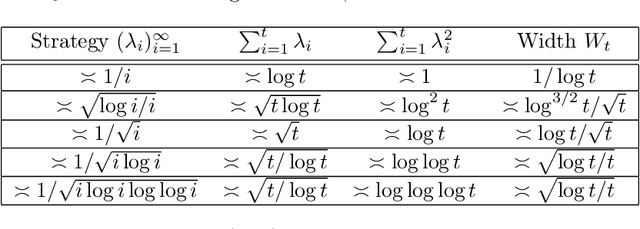
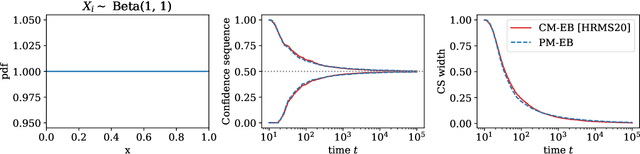
This paper derives confidence intervals (CI) and time-uniform confidence sequences (CS) for an unknown mean based on bounded observations. Our methods are based on a new general approach for deriving concentration bounds, that can be seen as a generalization (and improvement) of the classical Chernoff method. At its heart, it is based on deriving a new class of composite nonnegative martingales with initial value one, with strong connections to betting and the method of mixtures. We show how to extend these ideas to sampling without replacement. In all cases considered, the bounds are adaptive to the unknown variance, and empirically outperform competing approaches based on Hoeffding's or empirical Bernstein's inequalities and their recent supermartingale generalizations.

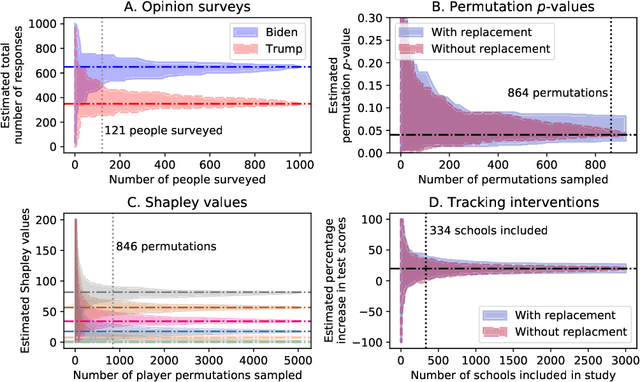
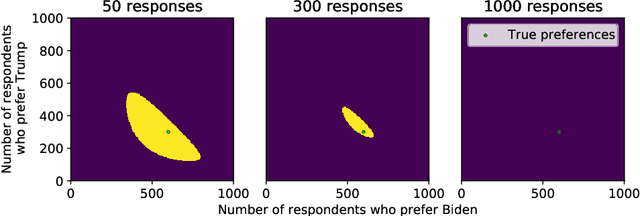
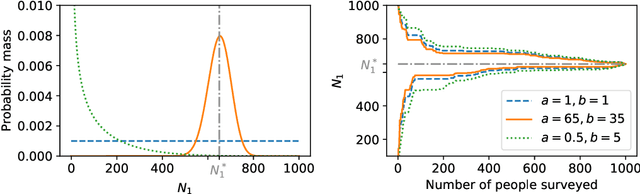
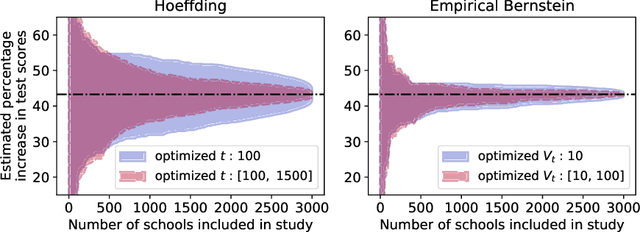
Confidence sequences for sampling without replacement

Many practical tasks involve sampling sequentially without replacement from a finite population of size $N$, in an attempt to estimate some parameter $\theta^\star$. Accurately quantifying uncertainty throughout this process is a nontrivial task, but is necessary because it often determines when we stop collecting samples and confidently report a result. We present a suite of tools to design confidence sequences (CS) for $\theta^\star$. A CS is a sequence of confidence sets $(C_n)_{n=1}^N$, that shrink in size, and all contain $\theta^\star$ simultaneously with high probability. We demonstrate their empirical performance using four example applications: local opinion surveys, calculating permutation $p$-values, estimating Shapley values, and tracking the effect of an intervention. We highlight two marked advantages over naive with-replacement sampling and/or uncertainty estimates: (1) each member of the finite population need only be queried once, saving time and money, and (2) our confidence sets are tighter and shrink to exactly zero width in $N$ steps.