Online monotone density estimation and log-optimal calibration

We study the problem of online monotone density estimation, where density estimators must be constructed in a predictable manner from sequentially observed data. We propose two online estimators: an online analogue of the classical Grenander estimator, and an expert aggregation estimator inspired by exponential weighting methods from the online learning literature. In the well-specified stochastic setting, where the underlying density is monotone, we show that the expected cumulative log-likelihood gap between the online estimators and the true density admits an $O(n^{1/3})$ bound. We further establish a $\sqrt{n\log{n}}$ pathwise regret bound for the expert aggregation estimator relative to the best offline monotone estimator chosen in hindsight, under minimal regularity assumptions on the observed sequence. As an application of independent interest, we show that the problem of constructing log-optimal p-to-e calibrators for sequential hypothesis testing can be formulated as an online monotone density estimation problem. We adapt the proposed estimators to build empirically adaptive p-to-e calibrators and establish their optimality. Numerical experiments illustrate the theoretical results.

Operationalizing Stein's Method for Online Linear Optimization: CLT-Based Optimal Tradeoffs

Adversarial online linear optimization (OLO) is essentially about making performance tradeoffs with respect to the unknown difficulty of the adversary. In the setting of one-dimensional fixed-time OLO on a bounded domain, it has been observed since Cover (1966) that achievable tradeoffs are governed by probabilistic inequalities, and these descriptive results can be converted into algorithms via dynamic programming, which, however, is not computationally efficient. We address this limitation by showing that Stein's method, a classical framework underlying the proofs of probabilistic limit theorems, can be operationalized as computationally efficient OLO algorithms. The associated regret and total loss upper bounds are "additively sharp", meaning that they surpass the conventional big-O optimality and match normal-approximation-based lower bounds by additive lower order terms. Our construction is inspired by the remarkably clean proof of a Wasserstein martingale central limit theorem (CLT) due to Röllin (2018). Several concrete benefits can be obtained from this general technique. First, with the same computational complexity, the proposed algorithm improves upon the total loss upper bounds of online gradient descent (OGD) and multiplicative weight update (MWU). Second, our algorithm can realize a continuum of optimal two-point tradeoffs between the total loss and the maximum regret over comparators, improving upon prior works in parameter-free online learning. Third, by allowing the adversary to randomize on an unbounded support, we achieve sharp in-expectation performance guarantees for OLO with noisy feedback.

An Asymptotic Law of the Iterated Logarithm for $\mathrm{KL}_{\inf}$

The population $\mathrm{KL}_{\inf}$ is a fundamental quantity that appears in lower bounds for (asymptotically) optimal regret of pure-exploration stochastic bandit algorithms, and optimal stopping time of sequential tests. Motivated by this, an empirical $\mathrm{KL}_{\inf}$ statistic is frequently used in the design of (asymptotically) optimal bandit algorithms and sequential tests. While nonasymptotic concentration bounds for the empirical $\mathrm{KL}_{\inf}$ have been developed, their optimality in terms of constants and rates is questionable, and their generality is limited (usually to bounded observations). The fundamental limits of nonasymptotic concentration are often described by the asymptotic fluctuations of the statistics. With that motivation, this paper presents a tight (upper and lower) law of the iterated logarithm for empirical $\mathrm{KL}_{\inf}$ applying to extremely general (unbounded) data.

Asymptotically optimal sequential change detection for bounded means

We consider the problem of quickest changepoint detection under the Average Run Length (ARL) constraint where the pre-change and post-change laws lie in composite families $\mathscr{P}$ and $\mathscr{Q}$ respectively. In such a problem, a massive challenge is characterizing the best possible detection delay when the "hardest" pre-change law in $\mathscr{P}$ depends on the unknown post-change law $Q\in\mathscr{Q}$. And typical simple-hypothesis likelihood-ratio arguments for Page-CUSUM and Shiryaev-Roberts do not at all apply here. To that end, we derive a universal sharp lower bound in full generality for any ARL-calibrated changepoint detector in the low type-I error ($γ\to\infty$ regime) of the order $\log(γ)/\mathrm{KL}_{\mathrm{inf}}(Q,\mathscr{P})$. We show achievability of this universal lower bound by proving a tight matching upper bound (with the same sharp $\logγ$ constant) in the important bounded mean detection setting. In addition, for separated mean shifts, we also we derive a uniform minimax guarantee of this achievability over the alternatives.

Eventually LIL Regret: Almost Sure $\ln\ln T$ Regret for a sub-Gaussian Mixture on Unbounded Data

We prove that a classic sub-Gaussian mixture proposed by Robbins in a stochastic setting actually satisfies a path-wise (deterministic) regret bound. For every path in a natural ``Ville event'' $E_α$, this regret till time $T$ is bounded by $\ln^2(1/α)/V_T + \ln (1/α) + \ln \ln V_T$ up to universal constants, where $V_T$ is a nonnegative, nondecreasing, cumulative variance process. (The bound reduces to $\ln(1/α) + \ln \ln V_T$ if $V_T \geq \ln(1/α)$.) If the data were stochastic, then one can show that $E_α$ has probability at least $1-α$ under a wide class of distributions (eg: sub-Gaussian, symmetric, variance-bounded, etc.). In fact, we show that on the Ville event $E_0$ of probability one, the regret on every path in $E_0$ is eventually bounded by $\ln \ln V_T$ (up to constants). We explain how this work helps bridge the world of adversarial online learning (which usually deals with regret bounds for bounded data), with game-theoretic statistics (which can handle unbounded data, albeit using stochastic assumptions). In short, conditional regret bounds serve as a bridge between stochastic and adversarial betting.

Vector-valued self-normalized concentration inequalities beyond sub-Gaussianity

The study of self-normalized processes plays a crucial role in a wide range of applications, from sequential decision-making to econometrics. While the behavior of self-normalized concentration has been widely investigated for scalar-valued processes, vector-valued processes remain comparatively underexplored, especially outside of the sub-Gaussian framework. In this contribution, we provide concentration bounds for self-normalized processes with light tails beyond sub-Gaussianity (such as Bennett or Bernstein bounds). We illustrate the relevance of our results in the context of online linear regression, with applications in (kernelized) linear bandits.

Adaptive Off-Policy Inference for M-Estimators Under Model Misspecification

When data are collected adaptively, such as in bandit algorithms, classical statistical approaches such as ordinary least squares and $M$-estimation will often fail to achieve asymptotic normality. Although recent lines of work have modified the classical approaches to ensure valid inference on adaptively collected data, most of these works assume that the model is correctly specified. We propose a method that provides valid inference for M-estimators that use adaptively collected bandit data with a (possibly) misspecified working model. A key ingredient in our approach is the use of flexible machine learning approaches to stabilize the variance induced by adaptive data collection. A major novelty is that our procedure enables the construction of valid confidence sets even in settings where treatment policies are unstable and non-converging, such as when there is no unique optimal arm and standard bandit algorithms are used. Empirical results on semi-synthetic datasets constructed from the Osteoarthritis Initiative demonstrate that the method maintains type I error control, while existing methods for inference in adaptive settings do not cover in the misspecified case.

Sequentially Auditing Differential Privacy

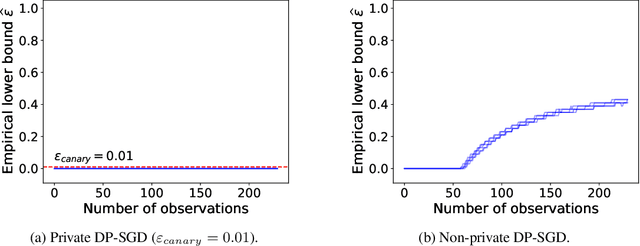
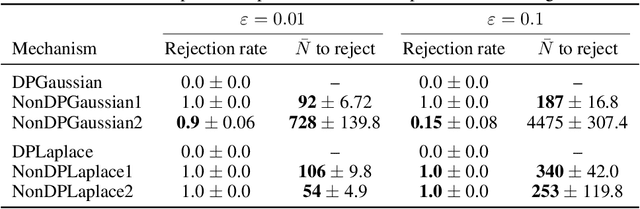
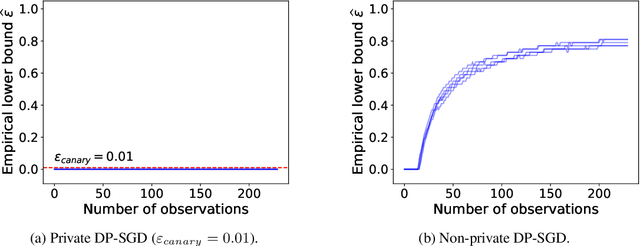
We propose a practical sequential test for auditing differential privacy guarantees of black-box mechanisms. The test processes streams of mechanisms' outputs providing anytime-valid inference while controlling Type I error, overcoming the fixed sample size limitation of previous batch auditing methods. Experiments show this test detects violations with sample sizes that are orders of magnitude smaller than existing methods, reducing this number from 50K to a few hundred examples, across diverse realistic mechanisms. Notably, it identifies DP-SGD privacy violations in \textit{under} one training run, unlike prior methods needing full model training.

A variational approach to dimension-free self-normalized concentration

We study the self-normalized concentration of vector-valued stochastic processes. We focus on bounds for sub-$\psi$ processes, a tail condition that encompasses a wide variety of well-known distributions (including sub-exponential, sub-Gaussian, sub-gamma, and sub-Poisson distributions). Our results recover and generalize the influential bound of Abbasi-Yadkori et al. (2011) and fill a gap in the literature between determinant-based bounds and those based on condition numbers. As applications we prove a Bernstein inequality for random vectors satisfying a moment condition (which is more general than boundedness), and also provide the first dimension-free, self-normalized empirical Bernstein inequality. Our techniques are based on the variational (PAC-Bayes) approach to concentration.

Private Evolution Converges

Private Evolution (PE) is a promising training-free method for differentially private (DP) synthetic data generation. While it achieves strong performance in some domains (e.g., images and text), its behavior in others (e.g., tabular data) is less consistent. To date, the only theoretical analysis of the convergence of PE depends on unrealistic assumptions about both the algorithm's behavior and the structure of the sensitive dataset. In this work, we develop a new theoretical framework to explain PE's practical behavior and identify sufficient conditions for its convergence. For $d$-dimensional sensitive datasets with $n$ data points from a bounded domain, we prove that PE produces an $(\epsilon, \delta)$-DP synthetic dataset with expected 1-Wasserstein distance of order $\tilde{O}(d(n\epsilon)^{-1/d})$ from the original, establishing worst-case convergence of the algorithm as $n \to \infty$. Our analysis extends to general Banach spaces as well. We also connect PE to the Private Signed Measure Mechanism, a method for DP synthetic data generation that has thus far not seen much practical adoption. We demonstrate the practical relevance of our theoretical findings in simulations.