Tomás González
Sequentially Auditing Differential Privacy
Sep 08, 2025
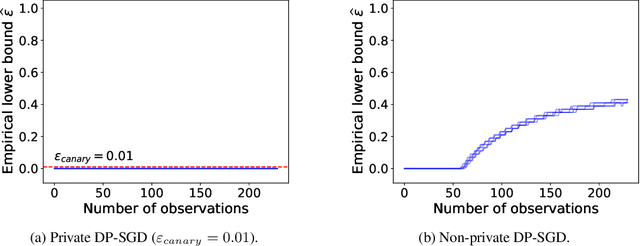
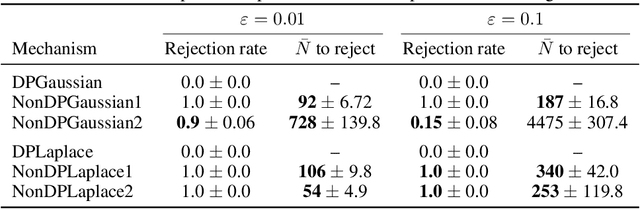
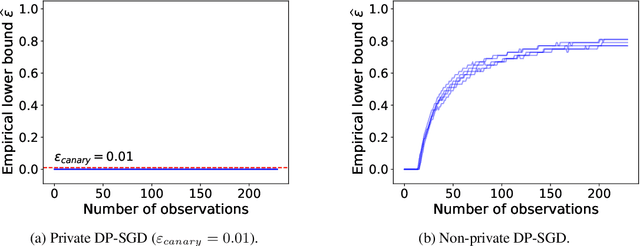
Abstract:We propose a practical sequential test for auditing differential privacy guarantees of black-box mechanisms. The test processes streams of mechanisms' outputs providing anytime-valid inference while controlling Type I error, overcoming the fixed sample size limitation of previous batch auditing methods. Experiments show this test detects violations with sample sizes that are orders of magnitude smaller than existing methods, reducing this number from 50K to a few hundred examples, across diverse realistic mechanisms. Notably, it identifies DP-SGD privacy violations in \textit{under} one training run, unlike prior methods needing full model training.
Private Evolution Converges
Jun 10, 2025Abstract:Private Evolution (PE) is a promising training-free method for differentially private (DP) synthetic data generation. While it achieves strong performance in some domains (e.g., images and text), its behavior in others (e.g., tabular data) is less consistent. To date, the only theoretical analysis of the convergence of PE depends on unrealistic assumptions about both the algorithm's behavior and the structure of the sensitive dataset. In this work, we develop a new theoretical framework to explain PE's practical behavior and identify sufficient conditions for its convergence. For $d$-dimensional sensitive datasets with $n$ data points from a bounded domain, we prove that PE produces an $(\epsilon, \delta)$-DP synthetic dataset with expected 1-Wasserstein distance of order $\tilde{O}(d(n\epsilon)^{-1/d})$ from the original, establishing worst-case convergence of the algorithm as $n \to \infty$. Our analysis extends to general Banach spaces as well. We also connect PE to the Private Signed Measure Mechanism, a method for DP synthetic data generation that has thus far not seen much practical adoption. We demonstrate the practical relevance of our theoretical findings in simulations.
Mirror Descent Algorithms with Nearly Dimension-Independent Rates for Differentially-Private Stochastic Saddle-Point Problems
Mar 05, 2024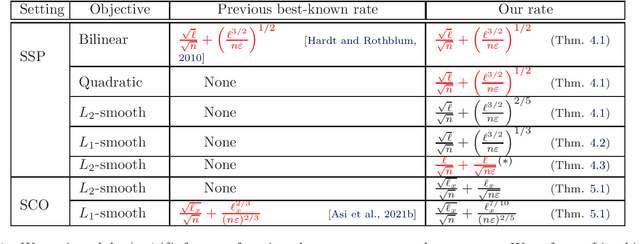
Abstract:We study the problem of differentially-private (DP) stochastic (convex-concave) saddle-points in the polyhedral setting. We propose $(\varepsilon, \delta)$-DP algorithms based on stochastic mirror descent that attain nearly dimension-independent convergence rates for the expected duality gap, a type of guarantee that was known before only for bilinear objectives. For convex-concave and first-order-smooth stochastic objectives, our algorithms attain a rate of $\sqrt{\log(d)/n} + (\log(d)^{3/2}/[n\varepsilon])^{1/3}$, where $d$ is the dimension of the problem and $n$ the dataset size. Under an additional second-order-smoothness assumption, we improve the rate on the expected gap to $\sqrt{\log(d)/n} + (\log(d)^{3/2}/[n\varepsilon])^{2/5}$. Under this additional assumption, we also show, by using bias-reduced gradient estimators, that the duality gap is bounded by $\log(d)/\sqrt{n} + \log(d)/[n\varepsilon]^{1/2}$ with constant success probability. This result provides evidence of the near-optimality of the approach. Finally, we show that combining our methods with acceleration techniques from online learning leads to the first algorithm for DP Stochastic Convex Optimization in the polyhedral setting that is not based on Frank-Wolfe methods. For convex and first-order-smooth stochastic objectives, our algorithms attain an excess risk of $\sqrt{\log(d)/n} + \log(d)^{7/10}/[n\varepsilon]^{2/5}$, and when additionally assuming second-order-smoothness, we improve the rate to $\sqrt{\log(d)/n} + \log(d)/\sqrt{n\varepsilon}$. Instrumental to all of these results are various extensions of the classical Maurey Sparsification Lemma, which may be of independent interest.
Faster Rates of Convergence to Stationary Points in Differentially Private Optimization
Jun 02, 2022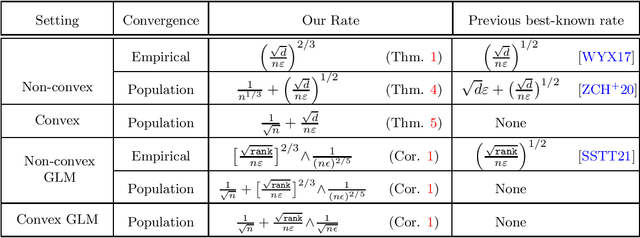
Abstract:We study the problem of approximating stationary points of Lipschitz and smooth functions under $(\varepsilon,\delta)$-differential privacy (DP) in both the finite-sum and stochastic settings. A point $\widehat{w}$ is called an $\alpha$-stationary point of a function $F:\mathbb{R}^d\rightarrow\mathbb{R}$ if $\|\nabla F(\widehat{w})\|\leq \alpha$. We provide a new efficient algorithm that finds an $\tilde{O}\big(\big[\frac{\sqrt{d}}{n\varepsilon}\big]^{2/3}\big)$-stationary point in the finite-sum setting, where $n$ is the number of samples. This improves on the previous best rate of $\tilde{O}\big(\big[\frac{\sqrt{d}}{n\varepsilon}\big]^{1/2}\big)$. We also give a new construction that improves over the existing rates in the stochastic optimization setting, where the goal is to find approximate stationary points of the population risk. Our construction finds a $\tilde{O}\big(\frac{1}{n^{1/3}} + \big[\frac{\sqrt{d}}{n\varepsilon}\big]^{1/2}\big)$-stationary point of the population risk in time linear in $n$. Furthermore, under the additional assumption of convexity, we completely characterize the sample complexity of finding stationary points of the population risk (up to polylog factors) and show that the optimal rate on population stationarity is $\tilde \Theta\big(\frac{1}{\sqrt{n}}+\frac{\sqrt{d}}{n\varepsilon}\big)$. Finally, we show that our methods can be used to provide dimension-independent rates of $O\big(\frac{1}{\sqrt{n}}+\min\big(\big[\frac{\sqrt{rank}}{n\varepsilon}\big]^{2/3},\frac{1}{(n\varepsilon)^{2/5}}\big)\big)$ on population stationarity for Generalized Linear Models (GLM), where $rank$ is the rank of the design matrix, which improves upon the previous best known rate.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge