Private Algorithms for Stochastic Saddle Points and Variational Inequalities: Beyond Euclidean Geometry

In this work, we conduct a systematic study of stochastic saddle point problems (SSP) and stochastic variational inequalities (SVI) under the constraint of $(\epsilon,\delta)$-differential privacy (DP) in both Euclidean and non-Euclidean setups. We first consider Lipschitz convex-concave SSPs in the $\ell_p/\ell_q$ setup, $p,q\in[1,2]$. Here, we obtain a bound of $\tilde{O}\big(\frac{1}{\sqrt{n}} + \frac{\sqrt{d}}{n\epsilon}\big)$ on the strong SP-gap, where $n$ is the number of samples and $d$ is the dimension. This rate is nearly optimal for any $p,q\in[1,2]$. Without additional assumptions, such as smoothness or linearity requirements, prior work under DP has only obtained this rate when $p=q=2$ (i.e., only in the Euclidean setup). Further, existing algorithms have each only been shown to work for specific settings of $p$ and $q$ and under certain assumptions on the loss and the feasible set, whereas we provide a general algorithm for DP SSPs whenever $p,q\in[1,2]$. Our result is obtained via a novel analysis of the recursive regularization algorithm. In particular, we develop new tools for analyzing generalization, which may be of independent interest. Next, we turn our attention towards SVIs with a monotone, bounded and Lipschitz operator and consider $\ell_p$-setups, $p\in[1,2]$. Here, we provide the first analysis which obtains a bound on the strong VI-gap of $\tilde{O}\big(\frac{1}{\sqrt{n}} + \frac{\sqrt{d}}{n\epsilon}\big)$. For $p-1=\Omega(1)$, this rate is near optimal due to existing lower bounds. To obtain this result, we develop a modified version of recursive regularization. Our analysis builds on the techniques we develop for SSPs as well as employing additional novel components which handle difficulties arising from adapting the recursive regularization framework to SVIs.

Public-data Assisted Private Stochastic Optimization: Power and Limitations

We study the limits and capability of public-data assisted differentially private (PA-DP) algorithms. Specifically, we focus on the problem of stochastic convex optimization (SCO) with either labeled or unlabeled public data. For complete/labeled public data, we show that any $(\epsilon,\delta)$-PA-DP has excess risk $\tilde{\Omega}\big(\min\big\{\frac{1}{\sqrt{n_{\text{pub}}}},\frac{1}{\sqrt{n}}+\frac{\sqrt{d}}{n\epsilon} \big\} \big)$, where $d$ is the dimension, ${n_{\text{pub}}}$ is the number of public samples, ${n_{\text{priv}}}$ is the number of private samples, and $n={n_{\text{pub}}}+{n_{\text{priv}}}$. These lower bounds are established via our new lower bounds for PA-DP mean estimation, which are of a similar form. Up to constant factors, these lower bounds show that the simple strategy of either treating all data as private or discarding the private data, is optimal. We also study PA-DP supervised learning with \textit{unlabeled} public samples. In contrast to our previous result, we here show novel methods for leveraging public data in private supervised learning. For generalized linear models (GLM) with unlabeled public data, we show an efficient algorithm which, given $\tilde{O}({n_{\text{priv}}}\epsilon)$ unlabeled public samples, achieves the dimension independent rate $\tilde{O}\big(\frac{1}{\sqrt{{n_{\text{priv}}}}} + \frac{1}{\sqrt{{n_{\text{priv}}}\epsilon}}\big)$. We develop new lower bounds for this setting which shows that this rate cannot be improved with more public samples, and any fewer public samples leads to a worse rate. Finally, we provide extensions of this result to general hypothesis classes with finite fat-shattering dimension with applications to neural networks and non-Euclidean geometries.

Differentially Private Non-Convex Optimization under the KL Condition with Optimal Rates

We study private empirical risk minimization (ERM) problem for losses satisfying the $(\gamma,\kappa)$-Kurdyka-{\L}ojasiewicz (KL) condition. The Polyak-{\L}ojasiewicz (PL) condition is a special case of this condition when $\kappa=2$. Specifically, we study this problem under the constraint of $\rho$ zero-concentrated differential privacy (zCDP). When $\kappa\in[1,2]$ and the loss function is Lipschitz and smooth over a sufficiently large region, we provide a new algorithm based on variance reduced gradient descent that achieves the rate $\tilde{O}\big(\big(\frac{\sqrt{d}}{n\sqrt{\rho}}\big)^\kappa\big)$ on the excess empirical risk, where $n$ is the dataset size and $d$ is the dimension. We further show that this rate is nearly optimal. When $\kappa \geq 2$ and the loss is instead Lipschitz and weakly convex, we show it is possible to achieve the rate $\tilde{O}\big(\big(\frac{\sqrt{d}}{n\sqrt{\rho}}\big)^\kappa\big)$ with a private implementation of the proximal point method. When the KL parameters are unknown, we provide a novel modification and analysis of the noisy gradient descent algorithm and show that this algorithm achieves a rate of $\tilde{O}\big(\big(\frac{\sqrt{d}}{n\sqrt{\rho}}\big)^{\frac{2\kappa}{4-\kappa}}\big)$ adaptively, which is nearly optimal when $\kappa = 2$. We further show that, without assuming the KL condition, the same gradient descent algorithm can achieve fast convergence to a stationary point when the gradient stays sufficiently large during the run of the algorithm. Specifically, we show that this algorithm can approximate stationary points of Lipschitz, smooth (and possibly nonconvex) objectives with rate as fast as $\tilde{O}\big(\frac{\sqrt{d}}{n\sqrt{\rho}}\big)$ and never worse than $\tilde{O}\big(\big(\frac{\sqrt{d}}{n\sqrt{\rho}}\big)^{1/2}\big)$. The latter rate matches the best known rate for methods that do not rely on variance reduction.

Differentially Private Algorithms for the Stochastic Saddle Point Problem with Optimal Rates for the Strong Gap

We show that convex-concave Lipschitz stochastic saddle point problems (also known as stochastic minimax optimization) can be solved under the constraint of $(\epsilon,\delta)$-differential privacy with \emph{strong (primal-dual) gap} rate of $\tilde O\big(\frac{1}{\sqrt{n}} + \frac{\sqrt{d}}{n\epsilon}\big)$, where $n$ is the dataset size and $d$ is the dimension of the problem. This rate is nearly optimal, based on existing lower bounds in differentially private stochastic optimization. Specifically, we prove a tight upper bound on the strong gap via novel implementation and analysis of the recursive regularization technique repurposed for saddle point problems. We show that this rate can be attained with $O\big(\min\big\{\frac{n^2\epsilon^{1.5}}{\sqrt{d}}, n^{3/2}\big\}\big)$ gradient complexity, and $O(n)$ gradient complexity if the loss function is smooth. As a byproduct of our method, we develop a general algorithm that, given a black-box access to a subroutine satisfying a certain $\alpha$ primal-dual accuracy guarantee with respect to the empirical objective, gives a solution to the stochastic saddle point problem with a strong gap of $\tilde{O}(\alpha+\frac{1}{\sqrt{n}})$. We show that this $\alpha$-accuracy condition is satisfied by standard algorithms for the empirical saddle point problem such as the proximal point method and the stochastic gradient descent ascent algorithm. Further, we show that even for simple problems it is possible for an algorithm to have zero weak gap and suffer from $\Omega(1)$ strong gap. We also show that there exists a fundamental tradeoff between stability and accuracy. Specifically, we show that any $\Delta$-stable algorithm has empirical gap $\Omega\big(\frac{1}{\Delta n}\big)$, and that this bound is tight. This result also holds also more specifically for empirical risk minimization problems and may be of independent interest.

Faster Rates of Convergence to Stationary Points in Differentially Private Optimization

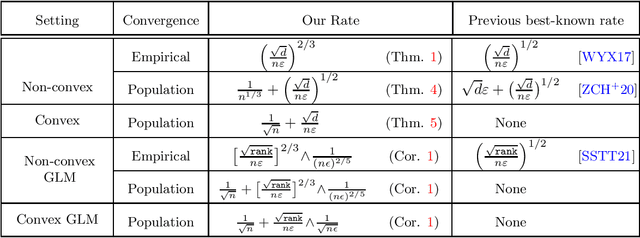
We study the problem of approximating stationary points of Lipschitz and smooth functions under $(\varepsilon,\delta)$-differential privacy (DP) in both the finite-sum and stochastic settings. A point $\widehat{w}$ is called an $\alpha$-stationary point of a function $F:\mathbb{R}^d\rightarrow\mathbb{R}$ if $\|\nabla F(\widehat{w})\|\leq \alpha$. We provide a new efficient algorithm that finds an $\tilde{O}\big(\big[\frac{\sqrt{d}}{n\varepsilon}\big]^{2/3}\big)$-stationary point in the finite-sum setting, where $n$ is the number of samples. This improves on the previous best rate of $\tilde{O}\big(\big[\frac{\sqrt{d}}{n\varepsilon}\big]^{1/2}\big)$. We also give a new construction that improves over the existing rates in the stochastic optimization setting, where the goal is to find approximate stationary points of the population risk. Our construction finds a $\tilde{O}\big(\frac{1}{n^{1/3}} + \big[\frac{\sqrt{d}}{n\varepsilon}\big]^{1/2}\big)$-stationary point of the population risk in time linear in $n$. Furthermore, under the additional assumption of convexity, we completely characterize the sample complexity of finding stationary points of the population risk (up to polylog factors) and show that the optimal rate on population stationarity is $\tilde \Theta\big(\frac{1}{\sqrt{n}}+\frac{\sqrt{d}}{n\varepsilon}\big)$. Finally, we show that our methods can be used to provide dimension-independent rates of $O\big(\frac{1}{\sqrt{n}}+\min\big(\big[\frac{\sqrt{rank}}{n\varepsilon}\big]^{2/3},\frac{1}{(n\varepsilon)^{2/5}}\big)\big)$ on population stationarity for Generalized Linear Models (GLM), where $rank$ is the rank of the design matrix, which improves upon the previous best known rate.

Differentially Private Generalized Linear Models Revisited

We study the problem of $(\epsilon,\delta)$-differentially private learning of linear predictors with convex losses. We provide results for two subclasses of loss functions. The first case is when the loss is smooth and non-negative but not necessarily Lipschitz (such as the squared loss). For this case, we establish an upper bound on the excess population risk of $\tilde{O}\left(\frac{\Vert w^*\Vert}{\sqrt{n}} + \min\left\{\frac{\Vert w^* \Vert^2}{(n\epsilon)^{2/3}},\frac{\sqrt{d}\Vert w^*\Vert^2}{n\epsilon}\right\}\right)$, where $n$ is the number of samples, $d$ is the dimension of the problem, and $w^*$ is the minimizer of the population risk. Apart from the dependence on $\Vert w^\ast\Vert$, our bound is essentially tight in all parameters. In particular, we show a lower bound of $\tilde{\Omega}\left(\frac{1}{\sqrt{n}} + {\min\left\{\frac{\Vert w^*\Vert^{4/3}}{(n\epsilon)^{2/3}}, \frac{\sqrt{d}\Vert w^*\Vert}{n\epsilon}\right\}}\right)$. We also revisit the previously studied case of Lipschitz losses [SSTT20]. For this case, we close the gap in the existing work and show that the optimal rate is (up to log factors) $\Theta\left(\frac{\Vert w^*\Vert}{\sqrt{n}} + \min\left\{\frac{\Vert w^*\Vert}{\sqrt{n\epsilon}},\frac{\sqrt{\text{rank}}\Vert w^*\Vert}{n\epsilon}\right\}\right)$, where $\text{rank}$ is the rank of the design matrix. This improves over existing work in the high privacy regime. Finally, our algorithms involve a private model selection approach that we develop to enable attaining the stated rates without a-priori knowledge of $\Vert w^*\Vert$.

Differentially Private Stochastic Optimization: New Results in Convex and Non-Convex Settings

We study differentially private stochastic optimization in convex and non-convex settings. For the convex case, we focus on the family of non-smooth generalized linear losses (GLLs). Our algorithm for the $\ell_2$ setting achieves optimal excess population risk in near-linear time, while the best known differentially private algorithms for general convex losses run in super-linear time. Our algorithm for the $\ell_1$ setting has nearly-optimal excess population risk $\tilde{O}\big(\sqrt{\frac{\log{d}}{n}}\big)$, and circumvents the dimension dependent lower bound of [AFKT21] for general non-smooth convex losses. In the differentially private non-convex setting, we provide several new algorithms for approximating stationary points of the population risk. For the $\ell_1$-case with smooth losses and polyhedral constraint, we provide the first nearly dimension independent rate, $\tilde O\big(\frac{\log^{2/3}{d}}{{n^{1/3}}}\big)$ in linear time. For the constrained $\ell_2$-case, with smooth losses, we obtain a linear-time algorithm with rate $\tilde O\big(\frac{1}{n^{3/10}d^{1/10}}+\big(\frac{d}{n^2}\big)^{1/5}\big)$. Finally, for the $\ell_2$-case we provide the first method for {\em non-smooth weakly convex} stochastic optimization with rate $\tilde O\big(\frac{1}{n^{1/4}}+\big(\frac{d}{n^2}\big)^{1/6}\big)$ which matches the best existing non-private algorithm when $d= O(\sqrt{n})$. We also extend all our results above for the non-convex $\ell_2$ setting to the $\ell_p$ setting, where $1 < p \leq 2$, with only polylogarithmic (in the dimension) overhead in the rates.