Mixing Times and Privacy Analysis for the Projected Langevin Algorithm under a Modulus of Continuity

We study the mixing time of the projected Langevin algorithm (LA) and the privacy curve of noisy Stochastic Gradient Descent (SGD), beyond nonexpansive iterations. Specifically, we derive new mixing time bounds for the projected LA which are, in some important cases, dimension-free and poly-logarithmic on the accuracy, closely matching the existing results in the smooth convex case. Additionally, we establish new upper bounds for the privacy curve of the subsampled noisy SGD algorithm. These bounds show a crucial dependency on the regularity of gradients, and are useful for a wide range of convex losses beyond the smooth case. Our analysis relies on a suitable extension of the Privacy Amplification by Iteration (PABI) framework (Feldman et al., 2018; Altschuler and Talwar, 2022, 2023) to noisy iterations whose gradient map is not necessarily nonexpansive. This extension is achieved by designing an optimization problem which accounts for the best possible R\'enyi divergence bound obtained by an application of PABI, where the tractability of the problem is crucially related to the modulus of continuity of the associated gradient mapping. We show that, in several interesting cases -- including the nonsmooth convex, weakly smooth and (strongly) dissipative -- such optimization problem can be solved exactly and explicitly. This yields the tightest possible PABI-based bounds, where our results are either new or substantially sharper than those in previous works.

Non-Euclidean High-Order Smooth Convex Optimization

We develop algorithms for the optimization of convex objectives that have H\"older continuous $q$-th derivatives with respect to a $p$-norm by using a $q$-th order oracle, for $p, q \geq 1$. We can also optimize other structured functions. We do this by developing a non-Euclidean inexact accelerated proximal point method that makes use of an inexact uniformly convex regularizer. We also provide nearly matching lower bounds for any deterministic algorithm that interacts with the function via a local oracle.

Private Algorithms for Stochastic Saddle Points and Variational Inequalities: Beyond Euclidean Geometry

In this work, we conduct a systematic study of stochastic saddle point problems (SSP) and stochastic variational inequalities (SVI) under the constraint of $(\epsilon,\delta)$-differential privacy (DP) in both Euclidean and non-Euclidean setups. We first consider Lipschitz convex-concave SSPs in the $\ell_p/\ell_q$ setup, $p,q\in[1,2]$. Here, we obtain a bound of $\tilde{O}\big(\frac{1}{\sqrt{n}} + \frac{\sqrt{d}}{n\epsilon}\big)$ on the strong SP-gap, where $n$ is the number of samples and $d$ is the dimension. This rate is nearly optimal for any $p,q\in[1,2]$. Without additional assumptions, such as smoothness or linearity requirements, prior work under DP has only obtained this rate when $p=q=2$ (i.e., only in the Euclidean setup). Further, existing algorithms have each only been shown to work for specific settings of $p$ and $q$ and under certain assumptions on the loss and the feasible set, whereas we provide a general algorithm for DP SSPs whenever $p,q\in[1,2]$. Our result is obtained via a novel analysis of the recursive regularization algorithm. In particular, we develop new tools for analyzing generalization, which may be of independent interest. Next, we turn our attention towards SVIs with a monotone, bounded and Lipschitz operator and consider $\ell_p$-setups, $p\in[1,2]$. Here, we provide the first analysis which obtains a bound on the strong VI-gap of $\tilde{O}\big(\frac{1}{\sqrt{n}} + \frac{\sqrt{d}}{n\epsilon}\big)$. For $p-1=\Omega(1)$, this rate is near optimal due to existing lower bounds. To obtain this result, we develop a modified version of recursive regularization. Our analysis builds on the techniques we develop for SSPs as well as employing additional novel components which handle difficulties arising from adapting the recursive regularization framework to SVIs.

Beyond Minimax Rates in Group Distributionally Robust Optimization via a Novel Notion of Sparsity

The minimax sample complexity of group distributionally robust optimization (GDRO) has been determined up to a $\log(K)$ factor, for $K$ the number of groups. In this work, we venture beyond the minimax perspective via a novel notion of sparsity that we dub $(\lambda, \beta)$-sparsity. In short, this condition means that at any parameter $\theta$, there is a set of at most $\beta$ groups whose risks at $\theta$ all are at least $\lambda$ larger than the risks of the other groups. To find an $\epsilon$-optimal $\theta$, we show via a novel algorithm and analysis that the $\epsilon$-dependent term in the sample complexity can swap a linear dependence on $K$ for a linear dependence on the potentially much smaller $\beta$. This improvement leverages recent progress in sleeping bandits, showing a fundamental connection between the two-player zero-sum game optimization framework for GDRO and per-action regret bounds in sleeping bandits. The aforementioned result assumes having a particular $\lambda$ as input. Perhaps surprisingly, we next show an adaptive algorithm which, up to log factors, gets sample complexity that adapts to the best $(\lambda, \beta)$-sparsity condition that holds. Finally, for a particular input $\lambda$, we also show how to get a dimension-free sample complexity result.

Tracking solutions of time-varying variational inequalities

Tracking the solution of time-varying variational inequalities is an important problem with applications in game theory, optimization, and machine learning. Existing work considers time-varying games or time-varying optimization problems. For strongly convex optimization problems or strongly monotone games, these results provide tracking guarantees under the assumption that the variation of the time-varying problem is restrained, that is, problems with a sublinear solution path. In this work we extend existing results in two ways: In our first result, we provide tracking bounds for (1) variational inequalities with a sublinear solution path but not necessarily monotone functions, and (2) for periodic time-varying variational inequalities that do not necessarily have a sublinear solution path-length. Our second main contribution is an extensive study of the convergence behavior and trajectory of discrete dynamical systems of periodic time-varying VI. We show that these systems can exhibit provably chaotic behavior or can converge to the solution. Finally, we illustrate our theoretical results with experiments.

Differentially Private Optimization with Sparse Gradients

Motivated by applications of large embedding models, we study differentially private (DP) optimization problems under sparsity of individual gradients. We start with new near-optimal bounds for the classic mean estimation problem but with sparse data, improving upon existing algorithms particularly for the high-dimensional regime. Building on this, we obtain pure- and approximate-DP algorithms with almost optimal rates for stochastic convex optimization with sparse gradients; the former represents the first nearly dimension-independent rates for this problem. Finally, we study the approximation of stationary points for the empirical loss in approximate-DP optimization and obtain rates that depend on sparsity instead of dimension, modulo polylogarithmic factors.

Optimization on a Finer Scale: Bounded Local Subgradient Variation Perspective

We initiate the study of nonsmooth optimization problems under bounded local subgradient variation, which postulates bounded difference between (sub)gradients in small local regions around points, in either average or maximum sense. The resulting class of objective functions encapsulates the classes of objective functions traditionally studied in optimization, which are defined based on either Lipschitz continuity of the objective or H\"{o}lder/Lipschitz continuity of its gradient. Further, the defined class contains functions that are neither Lipschitz continuous nor have a H\"{o}lder continuous gradient. When restricted to the traditional classes of optimization problems, the parameters defining the studied classes lead to more fine-grained complexity bounds, recovering traditional oracle complexity bounds in the worst case but generally leading to lower oracle complexity for functions that are not ``worst case.'' Some highlights of our results are that: (i) it is possible to obtain complexity results for both convex and nonconvex problems with the (local or global) Lipschitz constant being replaced by a constant of local subgradient variation and (ii) mean width of the subdifferential set around the optima plays a role in the complexity of nonsmooth optimization, particularly in parallel settings. A consequence of (ii) is that for any error parameter $\epsilon > 0$, parallel oracle complexity of nonsmooth Lipschitz convex optimization is lower than its sequential oracle complexity by a factor $\tilde{\Omega}\big(\frac{1}{\epsilon}\big)$ whenever the objective function is piecewise linear with polynomially many pieces in the input size. This is particularly surprising as existing parallel complexity lower bounds are based on such classes of functions. The seeming contradiction is resolved by considering the region in which the algorithm is allowed to query the objective.

Public-data Assisted Private Stochastic Optimization: Power and Limitations

We study the limits and capability of public-data assisted differentially private (PA-DP) algorithms. Specifically, we focus on the problem of stochastic convex optimization (SCO) with either labeled or unlabeled public data. For complete/labeled public data, we show that any $(\epsilon,\delta)$-PA-DP has excess risk $\tilde{\Omega}\big(\min\big\{\frac{1}{\sqrt{n_{\text{pub}}}},\frac{1}{\sqrt{n}}+\frac{\sqrt{d}}{n\epsilon} \big\} \big)$, where $d$ is the dimension, ${n_{\text{pub}}}$ is the number of public samples, ${n_{\text{priv}}}$ is the number of private samples, and $n={n_{\text{pub}}}+{n_{\text{priv}}}$. These lower bounds are established via our new lower bounds for PA-DP mean estimation, which are of a similar form. Up to constant factors, these lower bounds show that the simple strategy of either treating all data as private or discarding the private data, is optimal. We also study PA-DP supervised learning with \textit{unlabeled} public samples. In contrast to our previous result, we here show novel methods for leveraging public data in private supervised learning. For generalized linear models (GLM) with unlabeled public data, we show an efficient algorithm which, given $\tilde{O}({n_{\text{priv}}}\epsilon)$ unlabeled public samples, achieves the dimension independent rate $\tilde{O}\big(\frac{1}{\sqrt{{n_{\text{priv}}}}} + \frac{1}{\sqrt{{n_{\text{priv}}}\epsilon}}\big)$. We develop new lower bounds for this setting which shows that this rate cannot be improved with more public samples, and any fewer public samples leads to a worse rate. Finally, we provide extensions of this result to general hypothesis classes with finite fat-shattering dimension with applications to neural networks and non-Euclidean geometries.

Mirror Descent Algorithms with Nearly Dimension-Independent Rates for Differentially-Private Stochastic Saddle-Point Problems

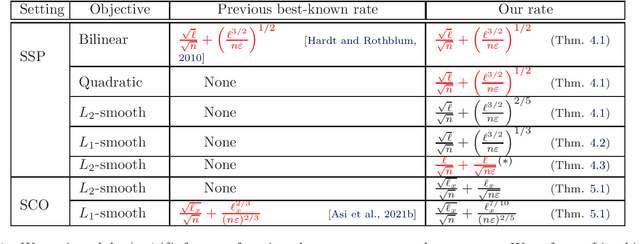
We study the problem of differentially-private (DP) stochastic (convex-concave) saddle-points in the polyhedral setting. We propose $(\varepsilon, \delta)$-DP algorithms based on stochastic mirror descent that attain nearly dimension-independent convergence rates for the expected duality gap, a type of guarantee that was known before only for bilinear objectives. For convex-concave and first-order-smooth stochastic objectives, our algorithms attain a rate of $\sqrt{\log(d)/n} + (\log(d)^{3/2}/[n\varepsilon])^{1/3}$, where $d$ is the dimension of the problem and $n$ the dataset size. Under an additional second-order-smoothness assumption, we improve the rate on the expected gap to $\sqrt{\log(d)/n} + (\log(d)^{3/2}/[n\varepsilon])^{2/5}$. Under this additional assumption, we also show, by using bias-reduced gradient estimators, that the duality gap is bounded by $\log(d)/\sqrt{n} + \log(d)/[n\varepsilon]^{1/2}$ with constant success probability. This result provides evidence of the near-optimality of the approach. Finally, we show that combining our methods with acceleration techniques from online learning leads to the first algorithm for DP Stochastic Convex Optimization in the polyhedral setting that is not based on Frank-Wolfe methods. For convex and first-order-smooth stochastic objectives, our algorithms attain an excess risk of $\sqrt{\log(d)/n} + \log(d)^{7/10}/[n\varepsilon]^{2/5}$, and when additionally assuming second-order-smoothness, we improve the rate to $\sqrt{\log(d)/n} + \log(d)/\sqrt{n\varepsilon}$. Instrumental to all of these results are various extensions of the classical Maurey Sparsification Lemma, which may be of independent interest.

Differentially Private Non-Convex Optimization under the KL Condition with Optimal Rates

We study private empirical risk minimization (ERM) problem for losses satisfying the $(\gamma,\kappa)$-Kurdyka-{\L}ojasiewicz (KL) condition. The Polyak-{\L}ojasiewicz (PL) condition is a special case of this condition when $\kappa=2$. Specifically, we study this problem under the constraint of $\rho$ zero-concentrated differential privacy (zCDP). When $\kappa\in[1,2]$ and the loss function is Lipschitz and smooth over a sufficiently large region, we provide a new algorithm based on variance reduced gradient descent that achieves the rate $\tilde{O}\big(\big(\frac{\sqrt{d}}{n\sqrt{\rho}}\big)^\kappa\big)$ on the excess empirical risk, where $n$ is the dataset size and $d$ is the dimension. We further show that this rate is nearly optimal. When $\kappa \geq 2$ and the loss is instead Lipschitz and weakly convex, we show it is possible to achieve the rate $\tilde{O}\big(\big(\frac{\sqrt{d}}{n\sqrt{\rho}}\big)^\kappa\big)$ with a private implementation of the proximal point method. When the KL parameters are unknown, we provide a novel modification and analysis of the noisy gradient descent algorithm and show that this algorithm achieves a rate of $\tilde{O}\big(\big(\frac{\sqrt{d}}{n\sqrt{\rho}}\big)^{\frac{2\kappa}{4-\kappa}}\big)$ adaptively, which is nearly optimal when $\kappa = 2$. We further show that, without assuming the KL condition, the same gradient descent algorithm can achieve fast convergence to a stationary point when the gradient stays sufficiently large during the run of the algorithm. Specifically, we show that this algorithm can approximate stationary points of Lipschitz, smooth (and possibly nonconvex) objectives with rate as fast as $\tilde{O}\big(\frac{\sqrt{d}}{n\sqrt{\rho}}\big)$ and never worse than $\tilde{O}\big(\big(\frac{\sqrt{d}}{n\sqrt{\rho}}\big)^{1/2}\big)$. The latter rate matches the best known rate for methods that do not rely on variance reduction.