Quantifying Cross-Modality Memorization in Vision-Language Models

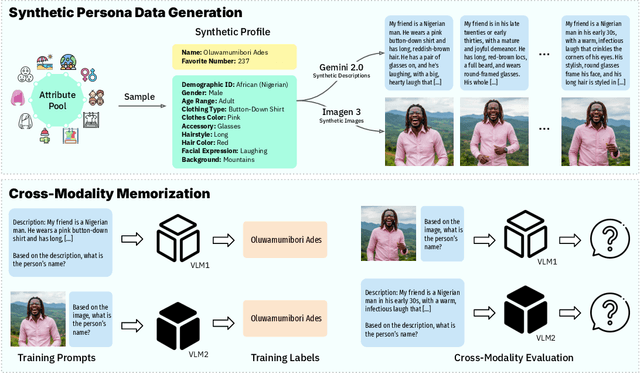
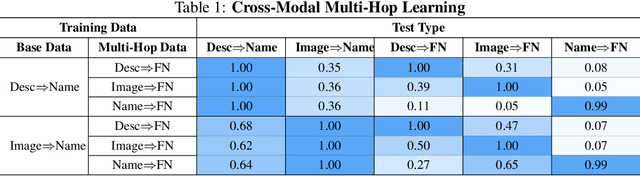
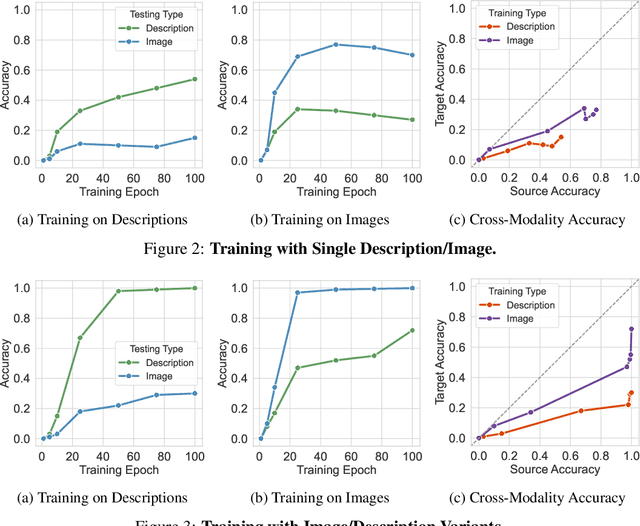
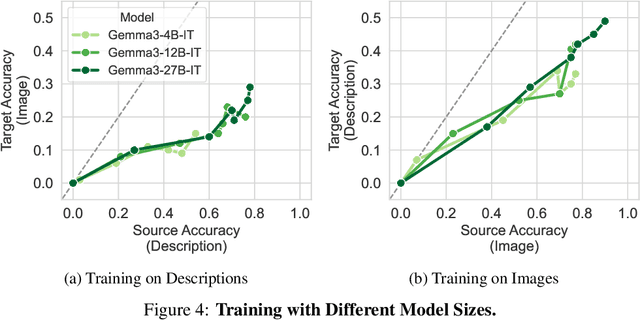
Understanding what and how neural networks memorize during training is crucial, both from the perspective of unintentional memorization of potentially sensitive information and from the standpoint of effective knowledge acquisition for real-world, knowledge-intensive tasks. While previous studies primarily investigate memorization within a single modality, such as text memorization in large language models or image memorization in diffusion models, unified multimodal models are becoming increasingly prevalent in practical applications. In this work, we focus on the unique characteristics of cross-modality memorization and conduct a systematic study centered on vision-language models. To facilitate controlled experiments, we first introduce a synthetic persona dataset comprising diverse synthetic person images and textual descriptions. We quantify factual knowledge memorization and cross-modal transferability by training models on a single modality and evaluating their performance in the other. Our results reveal that facts learned in one modality transfer to the other, but a significant gap exists between recalling information in the source and target modalities. Furthermore, we observe that this gap exists across various scenarios, including more capable models, machine unlearning, and the multi-hop case. At the end, we propose a baseline method to mitigate this challenge. We hope our study can inspire future research on developing more robust multimodal learning techniques to enhance cross-modal transferability.

Urania: Differentially Private Insights into AI Use

We introduce $Urania$, a novel framework for generating insights about LLM chatbot interactions with rigorous differential privacy (DP) guarantees. The framework employs a private clustering mechanism and innovative keyword extraction methods, including frequency-based, TF-IDF-based, and LLM-guided approaches. By leveraging DP tools such as clustering, partition selection, and histogram-based summarization, $Urania$ provides end-to-end privacy protection. Our evaluation assesses lexical and semantic content preservation, pair similarity, and LLM-based metrics, benchmarking against a non-private Clio-inspired pipeline (Tamkin et al., 2024). Moreover, we develop a simple empirical privacy evaluation that demonstrates the enhanced robustness of our DP pipeline. The results show the framework's ability to extract meaningful conversational insights while maintaining stringent user privacy, effectively balancing data utility with privacy preservation.

Combinatorial Optimization via LLM-driven Iterated Fine-tuning

We present a novel way to integrate flexible, context-dependent constraints into combinatorial optimization by leveraging Large Language Models (LLMs) alongside traditional algorithms. Although LLMs excel at interpreting nuanced, locally specified requirements, they struggle with enforcing global combinatorial feasibility. To bridge this gap, we propose an iterated fine-tuning framework where algorithmic feedback progressively refines the LLM's output distribution. Interpreting this as simulated annealing, we introduce a formal model based on a "coarse learnability" assumption, providing sample complexity bounds for convergence. Empirical evaluations on scheduling, graph connectivity, and clustering tasks demonstrate that our framework balances the flexibility of locally expressed constraints with rigorous global optimization more effectively compared to baseline sampling methods. Our results highlight a promising direction for hybrid AI-driven combinatorial reasoning.

PREM: Privately Answering Statistical Queries with Relative Error

We introduce $\mathsf{PREM}$ (Private Relative Error Multiplicative weight update), a new framework for generating synthetic data that achieves a relative error guarantee for statistical queries under $(\varepsilon, \delta)$ differential privacy (DP). Namely, for a domain ${\cal X}$, a family ${\cal F}$ of queries $f : {\cal X} \to \{0, 1\}$, and $\zeta > 0$, our framework yields a mechanism that on input dataset $D \in {\cal X}^n$ outputs a synthetic dataset $\widehat{D} \in {\cal X}^n$ such that all statistical queries in ${\cal F}$ on $D$, namely $\sum_{x \in D} f(x)$ for $f \in {\cal F}$, are within a $1 \pm \zeta$ multiplicative factor of the corresponding value on $\widehat{D}$ up to an additive error that is polynomial in $\log |{\cal F}|$, $\log |{\cal X}|$, $\log n$, $\log(1/\delta)$, $1/\varepsilon$, and $1/\zeta$. In contrast, any $(\varepsilon, \delta)$-DP mechanism is known to require worst-case additive error that is polynomial in at least one of $n, |{\cal F}|$, or $|{\cal X}|$. We complement our algorithm with nearly matching lower bounds.

Linear-Time User-Level DP-SCO via Robust Statistics

User-level differentially private stochastic convex optimization (DP-SCO) has garnered significant attention due to the paramount importance of safeguarding user privacy in modern large-scale machine learning applications. Current methods, such as those based on differentially private stochastic gradient descent (DP-SGD), often struggle with high noise accumulation and suboptimal utility due to the need to privatize every intermediate iterate. In this work, we introduce a novel linear-time algorithm that leverages robust statistics, specifically the median and trimmed mean, to overcome these challenges. Our approach uniquely bounds the sensitivity of all intermediate iterates of SGD with gradient estimation based on robust statistics, thereby significantly reducing the gradient estimation noise for privacy purposes and enhancing the privacy-utility trade-off. By sidestepping the repeated privatization required by previous methods, our algorithm not only achieves an improved theoretical privacy-utility trade-off but also maintains computational efficiency. We complement our algorithm with an information-theoretic lower bound, showing that our upper bound is optimal up to logarithmic factors and the dependence on $\epsilon$. This work sets the stage for more robust and efficient privacy-preserving techniques in machine learning, with implications for future research and application in the field.

Scaling Embedding Layers in Language Models

We propose SCONE ($\textbf{S}$calable, $\textbf{C}$ontextualized, $\textbf{O}$ffloaded, $\textbf{N}$-gram $\textbf{E}$mbedding), a method for extending input embedding layers to enhance language model performance as layer size scales. To avoid increased decoding costs, SCONE retains the original vocabulary while introducing embeddings for a set of frequent $n$-grams. These embeddings provide contextualized representation for each input token and are learned with a separate model during training. During inference, they are precomputed and stored in off-accelerator memory with minimal impact on inference speed. SCONE enables two new scaling strategies: increasing the number of cached $n$-gram embeddings and scaling the model used to learn them, all while maintaining fixed inference-time FLOPS. We show that scaling both aspects allows SCONE to outperform a 1.9B parameter baseline across diverse corpora, while using only half the inference-time FLOPS.

Scaling Laws for Differentially Private Language Models

Scaling laws have emerged as important components of large language model (LLM) training as they can predict performance gains through scale, and provide guidance on important hyper-parameter choices that would otherwise be expensive. LLMs also rely on large, high-quality training datasets, like those sourced from (sometimes sensitive) user data. Training models on this sensitive user data requires careful privacy protections like differential privacy (DP). However, the dynamics of DP training are significantly different, and consequently their scaling laws are not yet fully understood. In this work, we establish scaling laws that accurately model the intricacies of DP LLM training, providing a complete picture of the compute-privacy-utility tradeoffs and the optimal training configurations in many settings.

Balls-and-Bins Sampling for DP-SGD

We introduce the Balls-and-Bins sampling for differentially private (DP) optimization methods such as DP-SGD. While it has been common practice to use some form of shuffling in DP-SGD implementations, privacy accounting algorithms have typically assumed that Poisson subsampling is used instead. Recent work by Chua et al. (ICML 2024) however pointed out that shuffling based DP-SGD can have a much larger privacy cost in practical regimes of parameters. We show that the Balls-and-Bins sampling achieves the "best-of-both" samplers, namely, the implementation of Balls-and-Bins sampling is similar to that of Shuffling and models trained using DP-SGD with Balls-and-Bins sampling achieve utility comparable to those trained using DP-SGD with Shuffling at the same noise multiplier, and yet, Balls-and-Bins sampling enjoys similar-or-better privacy amplification as compared to Poisson subsampling in practical regimes.

LAuReL: Learned Augmented Residual Layer

One of the core pillars of efficient deep learning methods is architectural improvements such as the residual/skip connection, which has led to significantly better model convergence and quality. Since then the residual connection has become ubiquitous in not just convolutional neural networks but also transformer-based architectures, the backbone of LLMs. In this paper we introduce \emph{Learned Augmented Residual Layer} (LAuReL) -- a novel generalization of the canonical residual connection -- with the goal to be an in-situ replacement of the latter while outperforming on both model quality and footprint metrics. Our experiments show that using \laurel can help boost performance for both vision and language models. For example, on the ResNet-50, ImageNet 1K task, it achieves $60\%$ of the gains from adding an extra layer, while only adding $0.003\%$ more parameters, and matches it while adding $2.6\times$ fewer parameters.

Scalable DP-SGD: Shuffling vs. Poisson Subsampling

We provide new lower bounds on the privacy guarantee of the multi-epoch Adaptive Batch Linear Queries (ABLQ) mechanism with shuffled batch sampling, demonstrating substantial gaps when compared to Poisson subsampling; prior analysis was limited to a single epoch. Since the privacy analysis of Differentially Private Stochastic Gradient Descent (DP-SGD) is obtained by analyzing the ABLQ mechanism, this brings into serious question the common practice of implementing shuffling-based DP-SGD, but reporting privacy parameters as if Poisson subsampling was used. To understand the impact of this gap on the utility of trained machine learning models, we introduce a practical approach to implement Poisson subsampling at scale using massively parallel computation, and efficiently train models with the same. We compare the utility of models trained with Poisson-subsampling-based DP-SGD, and the optimistic estimates of utility when using shuffling, via our new lower bounds on the privacy guarantee of ABLQ with shuffling.