Daogao Liu
FlexOlmo: Open Language Models for Flexible Data Use
Jul 09, 2025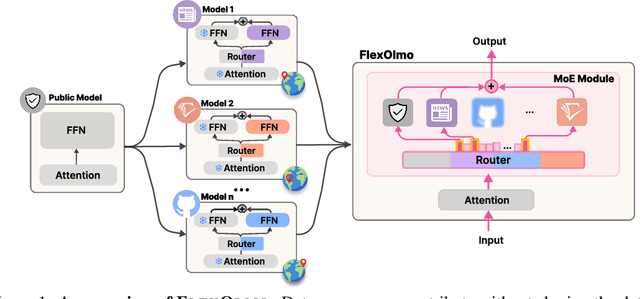
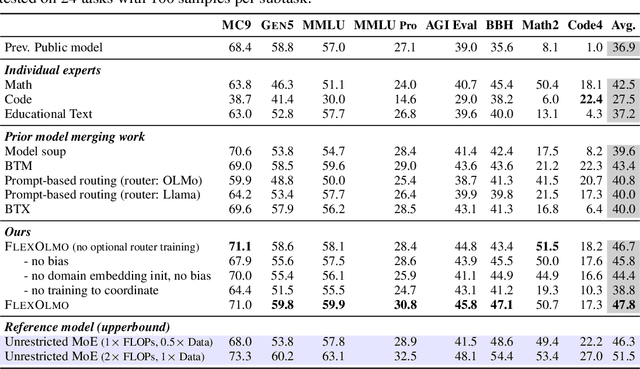
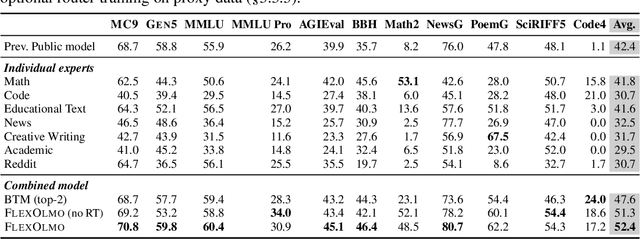
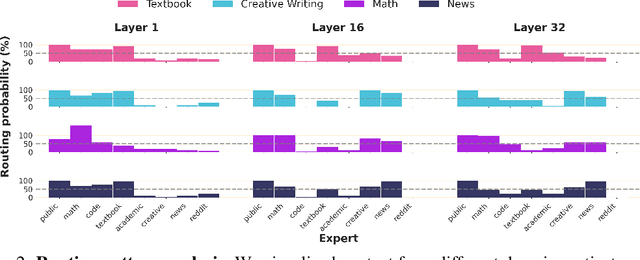
Abstract:We introduce FlexOlmo, a new class of language models (LMs) that supports (1) distributed training without data sharing, where different model parameters are independently trained on closed datasets, and (2) data-flexible inference, where these parameters along with their associated data can be flexibly included or excluded from model inferences with no further training. FlexOlmo employs a mixture-of-experts (MoE) architecture where each expert is trained independently on closed datasets and later integrated through a new domain-informed routing without any joint training. FlexOlmo is trained on FlexMix, a corpus we curate comprising publicly available datasets alongside seven domain-specific sets, representing realistic approximations of closed sets. We evaluate models with up to 37 billion parameters (20 billion active) on 31 diverse downstream tasks. We show that a general expert trained on public data can be effectively combined with independently trained experts from other data owners, leading to an average 41% relative improvement while allowing users to opt out of certain data based on data licensing or permission requirements. Our approach also outperforms prior model merging methods by 10.1% on average and surpasses the standard MoE trained without data restrictions using the same training FLOPs. Altogether, this research presents a solution for both data owners and researchers in regulated industries with sensitive or protected data. FlexOlmo enables benefiting from closed data while respecting data owners' preferences by keeping their data local and supporting fine-grained control of data access during inference.
Urania: Differentially Private Insights into AI Use
Jun 05, 2025Abstract:We introduce $Urania$, a novel framework for generating insights about LLM chatbot interactions with rigorous differential privacy (DP) guarantees. The framework employs a private clustering mechanism and innovative keyword extraction methods, including frequency-based, TF-IDF-based, and LLM-guided approaches. By leveraging DP tools such as clustering, partition selection, and histogram-based summarization, $Urania$ provides end-to-end privacy protection. Our evaluation assesses lexical and semantic content preservation, pair similarity, and LLM-based metrics, benchmarking against a non-private Clio-inspired pipeline (Tamkin et al., 2024). Moreover, we develop a simple empirical privacy evaluation that demonstrates the enhanced robustness of our DP pipeline. The results show the framework's ability to extract meaningful conversational insights while maintaining stringent user privacy, effectively balancing data utility with privacy preservation.
Private Geometric Median in Nearly-Linear Time
May 26, 2025Abstract:Estimating the geometric median of a dataset is a robust counterpart to mean estimation, and is a fundamental problem in computational geometry. Recently, [HSU24] gave an $(\varepsilon, \delta)$-differentially private algorithm obtaining an $\alpha$-multiplicative approximation to the geometric median objective, $\frac 1 n \sum_{i \in [n]} \|\cdot - \mathbf{x}_i\|$, given a dataset $\mathcal{D} := \{\mathbf{x}_i\}_{i \in [n]} \subset \mathbb{R}^d$. Their algorithm requires $n \gtrsim \sqrt d \cdot \frac 1 {\alpha\varepsilon}$ samples, which they prove is information-theoretically optimal. This result is surprising because its error scales with the \emph{effective radius} of $\mathcal{D}$ (i.e., of a ball capturing most points), rather than the worst-case radius. We give an improved algorithm that obtains the same approximation quality, also using $n \gtrsim \sqrt d \cdot \frac 1 {\alpha\epsilon}$ samples, but in time $\widetilde{O}(nd + \frac d {\alpha^2})$. Our runtime is nearly-linear, plus the cost of the cheapest non-private first-order method due to [CLM+16]. To achieve our results, we use subsampling and geometric aggregation tools inspired by FriendlyCore [TCK+22] to speed up the "warm start" component of the [HSU24] algorithm, combined with a careful custom analysis of DP-SGD's sensitivity for the geometric median objective.
Linear-Time User-Level DP-SCO via Robust Statistics
Feb 13, 2025Abstract:User-level differentially private stochastic convex optimization (DP-SCO) has garnered significant attention due to the paramount importance of safeguarding user privacy in modern large-scale machine learning applications. Current methods, such as those based on differentially private stochastic gradient descent (DP-SGD), often struggle with high noise accumulation and suboptimal utility due to the need to privatize every intermediate iterate. In this work, we introduce a novel linear-time algorithm that leverages robust statistics, specifically the median and trimmed mean, to overcome these challenges. Our approach uniquely bounds the sensitivity of all intermediate iterates of SGD with gradient estimation based on robust statistics, thereby significantly reducing the gradient estimation noise for privacy purposes and enhancing the privacy-utility trade-off. By sidestepping the repeated privatization required by previous methods, our algorithm not only achieves an improved theoretical privacy-utility trade-off but also maintains computational efficiency. We complement our algorithm with an information-theoretic lower bound, showing that our upper bound is optimal up to logarithmic factors and the dependence on $\epsilon$. This work sets the stage for more robust and efficient privacy-preserving techniques in machine learning, with implications for future research and application in the field.
Scaling Embedding Layers in Language Models
Feb 03, 2025Abstract:We propose SCONE ($\textbf{S}$calable, $\textbf{C}$ontextualized, $\textbf{O}$ffloaded, $\textbf{N}$-gram $\textbf{E}$mbedding), a method for extending input embedding layers to enhance language model performance as layer size scales. To avoid increased decoding costs, SCONE retains the original vocabulary while introducing embeddings for a set of frequent $n$-grams. These embeddings provide contextualized representation for each input token and are learned with a separate model during training. During inference, they are precomputed and stored in off-accelerator memory with minimal impact on inference speed. SCONE enables two new scaling strategies: increasing the number of cached $n$-gram embeddings and scaling the model used to learn them, all while maintaining fixed inference-time FLOPS. We show that scaling both aspects allows SCONE to outperform a 1.9B parameter baseline across diverse corpora, while using only half the inference-time FLOPS.
Faster Algorithms for User-Level Private Stochastic Convex Optimization
Oct 24, 2024
Abstract:We study private stochastic convex optimization (SCO) under user-level differential privacy (DP) constraints. In this setting, there are $n$ users (e.g., cell phones), each possessing $m$ data items (e.g., text messages), and we need to protect the privacy of each user's entire collection of data items. Existing algorithms for user-level DP SCO are impractical in many large-scale machine learning scenarios because: (i) they make restrictive assumptions on the smoothness parameter of the loss function and require the number of users to grow polynomially with the dimension of the parameter space; or (ii) they are prohibitively slow, requiring at least $(mn)^{3/2}$ gradient computations for smooth losses and $(mn)^3$ computations for non-smooth losses. To address these limitations, we provide novel user-level DP algorithms with state-of-the-art excess risk and runtime guarantees, without stringent assumptions. First, we develop a linear-time algorithm with state-of-the-art excess risk (for a non-trivial linear-time algorithm) under a mild smoothness assumption. Our second algorithm applies to arbitrary smooth losses and achieves optimal excess risk in $\approx (mn)^{9/8}$ gradient computations. Third, for non-smooth loss functions, we obtain optimal excess risk in $n^{11/8} m^{5/4}$ gradient computations. Moreover, our algorithms do not require the number of users to grow polynomially with the dimension.
Adaptive Batch Size for Privately Finding Second-Order Stationary Points
Oct 10, 2024Abstract:There is a gap between finding a first-order stationary point (FOSP) and a second-order stationary point (SOSP) under differential privacy constraints, and it remains unclear whether privately finding an SOSP is more challenging than finding an FOSP. Specifically, Ganesh et al. (2023) demonstrated that an $\alpha$-SOSP can be found with $\alpha=O(\frac{1}{n^{1/3}}+(\frac{\sqrt{d}}{n\epsilon})^{3/7})$, where $n$ is the dataset size, $d$ is the dimension, and $\epsilon$ is the differential privacy parameter. Building on the SpiderBoost algorithm framework, we propose a new approach that uses adaptive batch sizes and incorporates the binary tree mechanism. Our method improves the results for privately finding an SOSP, achieving $\alpha=O(\frac{1}{n^{1/3}}+(\frac{\sqrt{d}}{n\epsilon})^{1/2})$. This improved bound matches the state-of-the-art for finding an FOSP, suggesting that privately finding an SOSP may be achievable at no additional cost.
Improved Sample Complexity for Private Nonsmooth Nonconvex Optimization
Oct 08, 2024Abstract:We study differentially private (DP) optimization algorithms for stochastic and empirical objectives which are neither smooth nor convex, and propose methods that return a Goldstein-stationary point with sample complexity bounds that improve on existing works. We start by providing a single-pass $(\epsilon,\delta)$-DP algorithm that returns an $(\alpha,\beta)$-stationary point as long as the dataset is of size $\widetilde{\Omega}\left(1/\alpha\beta^{3}+d/\epsilon\alpha\beta^{2}+d^{3/4}/\epsilon^{1/2}\alpha\beta^{5/2}\right)$, which is $\Omega(\sqrt{d})$ times smaller than the algorithm of Zhang et al. [2024] for this task, where $d$ is the dimension. We then provide a multi-pass polynomial time algorithm which further improves the sample complexity to $\widetilde{\Omega}\left(d/\beta^2+d^{3/4}/\epsilon\alpha^{1/2}\beta^{3/2}\right)$, by designing a sample efficient ERM algorithm, and proving that Goldstein-stationary points generalize from the empirical loss to the population loss.
MUSE: Machine Unlearning Six-Way Evaluation for Language Models
Jul 08, 2024Abstract:Language models (LMs) are trained on vast amounts of text data, which may include private and copyrighted content. Data owners may request the removal of their data from a trained model due to privacy or copyright concerns. However, exactly unlearning only these datapoints (i.e., retraining with the data removed) is intractable in modern-day models. This has led to the development of many approximate unlearning algorithms. The evaluation of the efficacy of these algorithms has traditionally been narrow in scope, failing to precisely quantify the success and practicality of the algorithm from the perspectives of both the model deployers and the data owners. We address this issue by proposing MUSE, a comprehensive machine unlearning evaluation benchmark that enumerates six diverse desirable properties for unlearned models: (1) no verbatim memorization, (2) no knowledge memorization, (3) no privacy leakage, (4) utility preservation on data not intended for removal, (5) scalability with respect to the size of removal requests, and (6) sustainability over sequential unlearning requests. Using these criteria, we benchmark how effectively eight popular unlearning algorithms on 7B-parameter LMs can unlearn Harry Potter books and news articles. Our results demonstrate that most algorithms can prevent verbatim memorization and knowledge memorization to varying degrees, but only one algorithm does not lead to severe privacy leakage. Furthermore, existing algorithms fail to meet deployer's expectations because they often degrade general model utility and also cannot sustainably accommodate successive unlearning requests or large-scale content removal. Our findings identify key issues with the practicality of existing unlearning algorithms on language models, and we release our benchmark to facilitate further evaluations: muse-bench.github.io
Mind the Privacy Unit! User-Level Differential Privacy for Language Model Fine-Tuning
Jun 20, 2024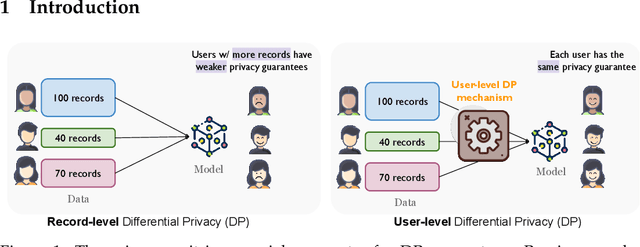
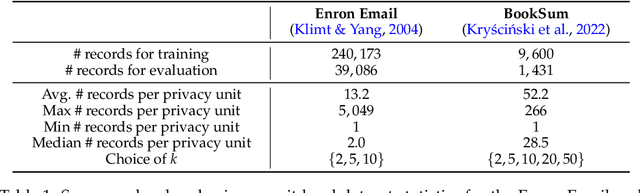

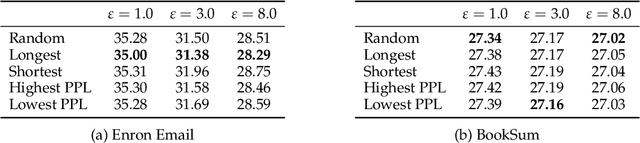
Abstract:Large language models (LLMs) have emerged as powerful tools for tackling complex tasks across diverse domains, but they also raise privacy concerns when fine-tuned on sensitive data due to potential memorization. While differential privacy (DP) offers a promising solution by ensuring models are `almost indistinguishable' with or without any particular privacy unit, current evaluations on LLMs mostly treat each example (text record) as the privacy unit. This leads to uneven user privacy guarantees when contributions per user vary. We therefore study user-level DP motivated by applications where it necessary to ensure uniform privacy protection across users. We present a systematic evaluation of user-level DP for LLM fine-tuning on natural language generation tasks. Focusing on two mechanisms for achieving user-level DP guarantees, Group Privacy and User-wise DP-SGD, we investigate design choices like data selection strategies and parameter tuning for the best privacy-utility tradeoff.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge