Instance-Optimality for Private KL Distribution Estimation

We study the fundamental problem of estimating an unknown discrete distribution $p$ over $d$ symbols, given $n$ i.i.d. samples from the distribution. We are interested in minimizing the KL divergence between the true distribution and the algorithm's estimate. We first construct minimax optimal private estimators. Minimax optimality however fails to shed light on an algorithm's performance on individual (non-worst-case) instances $p$ and simple minimax-optimal DP estimators can have poor empirical performance on real distributions. We then study this problem from an instance-optimality viewpoint, where the algorithm's error on $p$ is compared to the minimum achievable estimation error over a small local neighborhood of $p$. Under natural notions of local neighborhood, we propose algorithms that achieve instance-optimality up to constant factors, with and without a differential privacy constraint. Our upper bounds rely on (private) variants of the Good-Turing estimator. Our lower bounds use additive local neighborhoods that more precisely captures the hardness of distribution estimation in KL divergence, compared to ones considered in prior works.

Faster Rates for Private Adversarial Bandits

We design new differentially private algorithms for the problems of adversarial bandits and bandits with expert advice. For adversarial bandits, we give a simple and efficient conversion of any non-private bandit algorithm to a private bandit algorithm. Instantiating our conversion with existing non-private bandit algorithms gives a regret upper bound of $O\left(\frac{\sqrt{KT}}{\sqrt{\epsilon}}\right)$, improving upon the existing upper bound $O\left(\frac{\sqrt{KT \log(KT)}}{\epsilon}\right)$ for all $\epsilon \leq 1$. In particular, our algorithms allow for sublinear expected regret even when $\epsilon \leq \frac{1}{\sqrt{T}}$, establishing the first known separation between central and local differential privacy for this problem. For bandits with expert advice, we give the first differentially private algorithms, with expected regret $O\left(\frac{\sqrt{NT}}{\sqrt{\epsilon}}\right), O\left(\frac{\sqrt{KT\log(N)}\log(KT)}{\epsilon}\right)$, and $\tilde{O}\left(\frac{N^{1/6}K^{1/2}T^{2/3}\log(NT)}{\epsilon ^{1/3}} + \frac{N^{1/2}\log(NT)}{\epsilon}\right)$, where $K$ and $N$ are the number of actions and experts respectively. These rates allow us to get sublinear regret for different combinations of small and large $K, N$ and $\epsilon.$

On Privately Estimating a Single Parameter

We investigate differentially private estimators for individual parameters within larger parametric models. While generic private estimators exist, the estimators we provide repose on new local notions of estimand stability, and these notions allow procedures that provide private certificates of their own stability. By leveraging these private certificates, we provide computationally and statistical efficient mechanisms that release private statistics that are, at least asymptotically in the sample size, essentially unimprovable: they achieve instance optimal bounds. Additionally, we investigate the practicality of the algorithms both in simulated data and in real-world data from the American Community Survey and US Census, highlighting scenarios in which the new procedures are successful and identifying areas for future work.

PREAMBLE: Private and Efficient Aggregation of Block Sparse Vectors and Applications

We revisit the problem of secure aggregation of high-dimensional vectors in a two-server system such as Prio. These systems are typically used to aggregate vectors such as gradients in private federated learning, where the aggregate itself is protected via noise addition to ensure differential privacy. Existing approaches require communication scaling with the dimensionality, and thus limit the dimensionality of vectors one can efficiently process in this setup. We propose PREAMBLE: Private Efficient Aggregation Mechanism for BLock-sparse Euclidean Vectors. PREAMBLE is a novel extension of distributed point functions that enables communication- and computation-efficient aggregation of block-sparse vectors, which are sparse vectors where the non-zero entries occur in a small number of clusters of consecutive coordinates. We then show that PREAMBLE can be combined with random sampling and privacy amplification by sampling results, to allow asymptotically optimal privacy-utility trade-offs for vector aggregation, at a fraction of the communication cost. When coupled with recent advances in numerical privacy accounting, our approach incurs a negligible overhead in noise variance, compared to the Gaussian mechanism used with Prio.

Local Pan-Privacy for Federated Analytics

Pan-privacy was proposed by Dwork et al. as an approach to designing a private analytics system that retains its privacy properties in the face of intrusions that expose the system's internal state. Motivated by federated telemetry applications, we study local pan-privacy, where privacy should be retained under repeated unannounced intrusions on the local state. We consider the problem of monitoring the count of an event in a federated system, where event occurrences on a local device should be hidden even from an intruder on that device. We show that under reasonable constraints, the goal of providing information-theoretic differential privacy under intrusion is incompatible with collecting telemetry information. We then show that this problem can be solved in a scalable way using standard cryptographic primitives.

Fingerprinting Codes Meet Geometry: Improved Lower Bounds for Private Query Release and Adaptive Data Analysis

Fingerprinting codes are a crucial tool for proving lower bounds in differential privacy. They have been used to prove tight lower bounds for several fundamental questions, especially in the ``low accuracy'' regime. Unlike reconstruction/discrepancy approaches however, they are more suited for query sets that arise naturally from the fingerprinting codes construction. In this work, we propose a general framework for proving fingerprinting type lower bounds, that allows us to tailor the technique to the geometry of the query set. Our approach allows us to prove several new results, including the following. First, we show that any (sample- and population-)accurate algorithm for answering $Q$ arbitrary adaptive counting queries over a universe $\mathcal{X}$ to accuracy $\alpha$ needs $\Omega(\frac{\sqrt{\log |\mathcal{X}|}\cdot \log Q}{\alpha^3})$ samples, matching known upper bounds. This shows that the approaches based on differential privacy are optimal for this question, and improves significantly on the previously known lower bounds of $\frac{\log Q}{\alpha^2}$ and $\min(\sqrt{Q}, \sqrt{\log |\mathcal{X}|})/\alpha^2$. Second, we show that any $(\varepsilon,\delta)$-DP algorithm for answering $Q$ counting queries to accuracy $\alpha$ needs $\Omega(\frac{\sqrt{ \log|\mathcal{X}| \log(1/\delta)} \log Q}{\varepsilon\alpha^2})$ samples, matching known upper bounds up to constants. Our framework allows for proving this bound via a direct correlation analysis and improves the prior bound of [BUV'14] by $\sqrt{\log(1/\delta)}$. Third, we characterize the sample complexity of answering a set of random $0$-$1$ queries under approximate differential privacy. We give new upper and lower bounds in different regimes. By combining them with known results, we can complete the whole picture.

Privacy-Computation trade-offs in Private Repetition and Metaselection

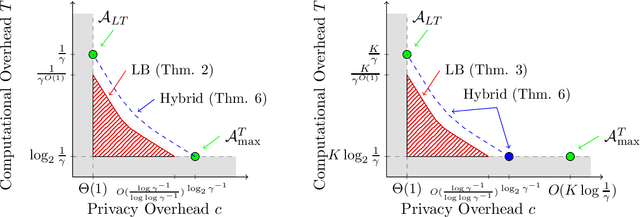
A Private Repetition algorithm takes as input a differentially private algorithm with constant success probability and boosts it to one that succeeds with high probability. These algorithms are closely related to private metaselection algorithms that compete with the best of many private algorithms, and private hyperparameter tuning algorithms that compete with the best hyperparameter settings for a private learning algorithm. Existing algorithms for these tasks pay either a large overhead in privacy cost, or a large overhead in computational cost. In this work, we show strong lower bounds for problems of this kind, showing in particular that for any algorithm that preserves the privacy cost up to a constant factor, the failure probability can only fall polynomially in the computational overhead. This is in stark contrast with the non-private setting, where the failure probability falls exponentially in the computational overhead. By carefully combining existing algorithms for metaselection, we prove computation-privacy tradeoffs that nearly match our lower bounds.

Adaptive Batch Size for Privately Finding Second-Order Stationary Points

There is a gap between finding a first-order stationary point (FOSP) and a second-order stationary point (SOSP) under differential privacy constraints, and it remains unclear whether privately finding an SOSP is more challenging than finding an FOSP. Specifically, Ganesh et al. (2023) demonstrated that an $\alpha$-SOSP can be found with $\alpha=O(\frac{1}{n^{1/3}}+(\frac{\sqrt{d}}{n\epsilon})^{3/7})$, where $n$ is the dataset size, $d$ is the dimension, and $\epsilon$ is the differential privacy parameter. Building on the SpiderBoost algorithm framework, we propose a new approach that uses adaptive batch sizes and incorporates the binary tree mechanism. Our method improves the results for privately finding an SOSP, achieving $\alpha=O(\frac{1}{n^{1/3}}+(\frac{\sqrt{d}}{n\epsilon})^{1/2})$. This improved bound matches the state-of-the-art for finding an FOSP, suggesting that privately finding an SOSP may be achievable at no additional cost.

Improved Sample Complexity for Private Nonsmooth Nonconvex Optimization

We study differentially private (DP) optimization algorithms for stochastic and empirical objectives which are neither smooth nor convex, and propose methods that return a Goldstein-stationary point with sample complexity bounds that improve on existing works. We start by providing a single-pass $(\epsilon,\delta)$-DP algorithm that returns an $(\alpha,\beta)$-stationary point as long as the dataset is of size $\widetilde{\Omega}\left(1/\alpha\beta^{3}+d/\epsilon\alpha\beta^{2}+d^{3/4}/\epsilon^{1/2}\alpha\beta^{5/2}\right)$, which is $\Omega(\sqrt{d})$ times smaller than the algorithm of Zhang et al. [2024] for this task, where $d$ is the dimension. We then provide a multi-pass polynomial time algorithm which further improves the sample complexity to $\widetilde{\Omega}\left(d/\beta^2+d^{3/4}/\epsilon\alpha^{1/2}\beta^{3/2}\right)$, by designing a sample efficient ERM algorithm, and proving that Goldstein-stationary points generalize from the empirical loss to the population loss.

Instance-Optimal Private Density Estimation in the Wasserstein Distance

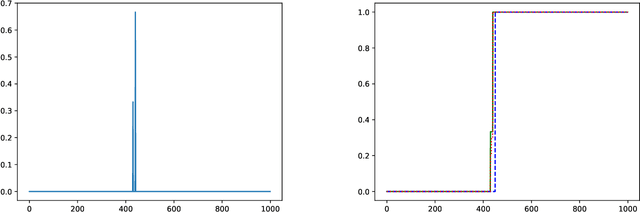
Estimating the density of a distribution from samples is a fundamental problem in statistics. In many practical settings, the Wasserstein distance is an appropriate error metric for density estimation. For example, when estimating population densities in a geographic region, a small Wasserstein distance means that the estimate is able to capture roughly where the population mass is. In this work we study differentially private density estimation in the Wasserstein distance. We design and analyze instance-optimal algorithms for this problem that can adapt to easy instances. For distributions $P$ over $\mathbb{R}$, we consider a strong notion of instance-optimality: an algorithm that uniformly achieves the instance-optimal estimation rate is competitive with an algorithm that is told that the distribution is either $P$ or $Q_P$ for some distribution $Q_P$ whose probability density function (pdf) is within a factor of 2 of the pdf of $P$. For distributions over $\mathbb{R}^2$, we use a different notion of instance optimality. We say that an algorithm is instance-optimal if it is competitive with an algorithm that is given a constant-factor multiplicative approximation of the density of the distribution. We characterize the instance-optimal estimation rates in both these settings and show that they are uniformly achievable (up to polylogarithmic factors). Our approach for $\mathbb{R}^2$ extends to arbitrary metric spaces as it goes via hierarchically separated trees. As a special case our results lead to instance-optimal private learning in TV distance for discrete distributions.