John C. Duchi
Prior Diffusiveness and Regret in the Linear-Gaussian Bandit
Jan 05, 2026Abstract:We prove that Thompson sampling exhibits $\tilde{O}(σd \sqrt{T} + d r \sqrt{\mathrm{Tr}(Σ_0)})$ Bayesian regret in the linear-Gaussian bandit with a $\mathcal{N}(μ_0, Σ_0)$ prior distribution on the coefficients, where $d$ is the dimension, $T$ is the time horizon, $r$ is the maximum $\ell_2$ norm of the actions, and $σ^2$ is the noise variance. In contrast to existing regret bounds, this shows that to within logarithmic factors, the prior-dependent ``burn-in'' term $d r \sqrt{\mathrm{Tr}(Σ_0)}$ decouples additively from the minimax (long run) regret $σd \sqrt{T}$. Previous regret bounds exhibit a multiplicative dependence on these terms. We establish these results via a new ``elliptical potential'' lemma, and also provide a lower bound indicating that the burn-in term is unavoidable.
Distribution free M-estimation
May 28, 2025Abstract:The basic question of delineating those statistical problems that are solvable without making any assumptions on the underlying data distribution has long animated statistics and learning theory. This paper characterizes when a (univariate) convex M-estimation or stochastic optimization problem is solvable in such an assumption-free setting, providing a precise dividing line between solvable and unsolvable problems. The conditions we identify show, perhaps surprisingly, that Lipschitz continuity of the loss being minimized is not necessary for distribution free minimization, and they are also distinct from classical characterizations of learnability in machine learning.
On Privately Estimating a Single Parameter
Mar 21, 2025



Abstract:We investigate differentially private estimators for individual parameters within larger parametric models. While generic private estimators exist, the estimators we provide repose on new local notions of estimand stability, and these notions allow procedures that provide private certificates of their own stability. By leveraging these private certificates, we provide computationally and statistical efficient mechanisms that release private statistics that are, at least asymptotically in the sample size, essentially unimprovable: they achieve instance optimal bounds. Additionally, we investigate the practicality of the algorithms both in simulated data and in real-world data from the American Community Survey and US Census, highlighting scenarios in which the new procedures are successful and identifying areas for future work.
Predictive Inference in Multi-environment Scenarios
Mar 25, 2024Abstract:We address the challenge of constructing valid confidence intervals and sets in problems of prediction across multiple environments. We investigate two types of coverage suitable for these problems, extending the jackknife and split-conformal methods to show how to obtain distribution-free coverage in such non-traditional, hierarchical data-generating scenarios. Our contributions also include extensions for settings with non-real-valued responses and a theory of consistency for predictive inference in these general problems. We demonstrate a novel resizing method to adapt to problem difficulty, which applies both to existing approaches for predictive inference with hierarchical data and the methods we develop; this reduces prediction set sizes using limited information from the test environment, a key to the methods' practical performance, which we evaluate through neurochemical sensing and species classification datasets.
PPI++: Efficient Prediction-Powered Inference
Nov 02, 2023Abstract:We present PPI++: a computationally lightweight methodology for estimation and inference based on a small labeled dataset and a typically much larger dataset of machine-learning predictions. The methods automatically adapt to the quality of available predictions, yielding easy-to-compute confidence sets -- for parameters of any dimensionality -- that always improve on classical intervals using only the labeled data. PPI++ builds on prediction-powered inference (PPI), which targets the same problem setting, improving its computational and statistical efficiency. Real and synthetic experiments demonstrate the benefits of the proposed adaptations.
The Lifecycle of a Statistical Model: Model Failure Detection, Identification, and Refitting
Feb 08, 2022



Abstract:The statistical machine learning community has demonstrated considerable resourcefulness over the years in developing highly expressive tools for estimation, prediction, and inference. The bedrock assumptions underlying these developments are that the data comes from a fixed population and displays little heterogeneity. But reality is significantly more complex: statistical models now routinely fail when released into real-world systems and scientific applications, where such assumptions rarely hold. Consequently, we pursue a different path in this paper vis-a-vis the well-worn trail of developing new methodology for estimation and prediction. In this paper, we develop tools and theory for detecting and identifying regions of the covariate space (subpopulations) where model performance has begun to degrade, and study intervening to fix these failures through refitting. We present empirical results with three real-world data sets -- including a time series involving forecasting the incidence of COVID-19 -- showing that our methodology generates interpretable results, is useful for tracking model performance, and can boost model performance through refitting. We complement these empirical results with theory proving that our methodology is minimax optimal for recovering anomalous subpopulations as well as refitting to improve accuracy in a structured normal means setting.
Accelerated, Optimal, and Parallel: Some Results on Model-Based Stochastic Optimization
Jan 07, 2021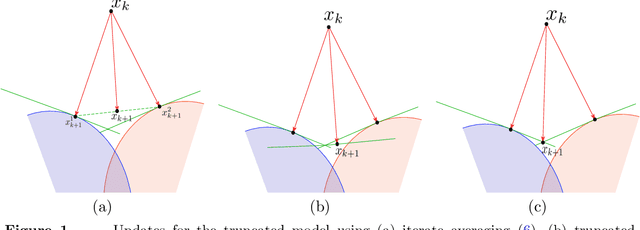
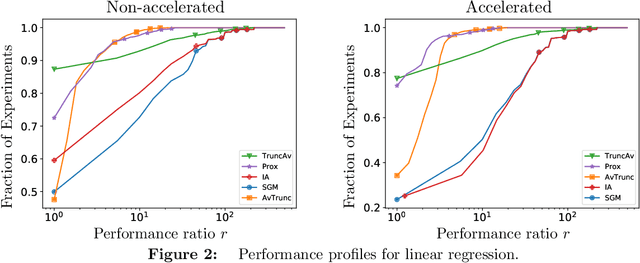
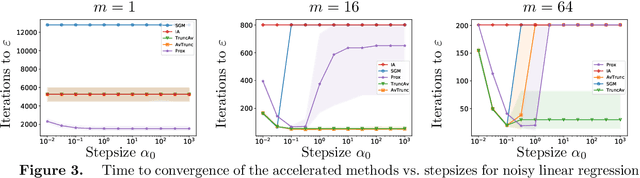
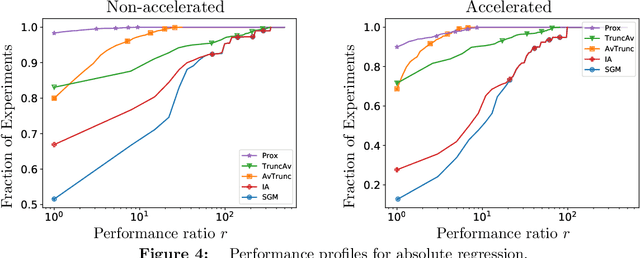
Abstract:We extend the Approximate-Proximal Point (aProx) family of model-based methods for solving stochastic convex optimization problems, including stochastic subgradient, proximal point, and bundle methods, to the minibatch and accelerated setting. To do so, we propose specific model-based algorithms and an acceleration scheme for which we provide non-asymptotic convergence guarantees, which are order-optimal in all problem-dependent constants and provide linear speedup in minibatch size, while maintaining the desirable robustness traits (e.g. to stepsize) of the aProx family. Additionally, we show improved convergence rates and matching lower bounds identifying new fundamental constants for "interpolation" problems, whose importance in statistical machine learning is growing; this, for example, gives a parallelization strategy for alternating projections. We corroborate our theoretical results with empirical testing to demonstrate the gains accurate modeling, acceleration, and minibatching provide.
Large-Scale Methods for Distributionally Robust Optimization
Oct 12, 2020



Abstract:We propose and analyze algorithms for distributionally robust optimization of convex losses with conditional value at risk (CVaR) and $\chi^2$ divergence uncertainty sets. We prove that our algorithms require a number of gradient evaluations independent of training set size and number of parameters, making them suitable for large-scale applications. For $\chi^2$ uncertainty sets these are the first such guarantees in the literature, and for CVaR our guarantees scale linearly in the uncertainty level rather than quadratically as in previous work. We also provide lower bounds proving the worst-case optimality of our algorithms for CVaR and a penalized version of the $\chi^2$ problem. Our primary technical contributions are novel bounds on the bias of batch robust risk estimation and the variance of a multilevel Monte Carlo gradient estimator due to [Blanchet & Glynn, 2015]. Experiments on MNIST and ImageNet confirm the theoretical scaling of our algorithms, which are 9--36 times more efficient than full-batch methods.
Robust Validation: Confident Predictions Even When Distributions Shift
Aug 10, 2020



Abstract:While the traditional viewpoint in machine learning and statistics assumes training and testing samples come from the same population, practice belies this fiction. One strategy---coming from robust statistics and optimization---is thus to build a model robust to distributional perturbations. In this paper, we take a different approach to describe procedures for robust predictive inference, where a model provides uncertainty estimates on its predictions rather than point predictions. We present a method that produces prediction sets (almost exactly) giving the right coverage level for any test distribution in an $f$-divergence ball around the training population. The method, based on conformal inference, achieves (nearly) valid coverage in finite samples, under only the condition that the training data be exchangeable. An essential component of our methodology is to estimate the amount of expected future data shift and build robustness to it; we develop estimators and prove their consistency for protection and validity of uncertainty estimates under shifts. By experimenting on several large-scale benchmark datasets, including Recht et al.'s CIFAR-v4 and ImageNet-V2 datasets, we provide complementary empirical results that highlight the importance of robust predictive validity.
Second-Order Information in Non-Convex Stochastic Optimization: Power and Limitations
Jun 24, 2020


Abstract:We design an algorithm which finds an $\epsilon$-approximate stationary point (with $\|\nabla F(x)\|\le \epsilon$) using $O(\epsilon^{-3})$ stochastic gradient and Hessian-vector products, matching guarantees that were previously available only under a stronger assumption of access to multiple queries with the same random seed. We prove a lower bound which establishes that this rate is optimal and---surprisingly---that it cannot be improved using stochastic $p$th order methods for any $p\ge 2$, even when the first $p$ derivatives of the objective are Lipschitz. Together, these results characterize the complexity of non-convex stochastic optimization with second-order methods and beyond. Expanding our scope to the oracle complexity of finding $(\epsilon,\gamma)$-approximate second-order stationary points, we establish nearly matching upper and lower bounds for stochastic second-order methods. Our lower bounds here are novel even in the noiseless case.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge