Closing the Computational-Query Depth Gap in Parallel Stochastic Convex Optimization

We develop a new parallel algorithm for minimizing Lipschitz, convex functions with a stochastic subgradient oracle. The total number of queries made and the query depth, i.e., the number of parallel rounds of queries, match the prior state-of-the-art, [CJJLLST23], while improving upon the computational depth by a polynomial factor for sufficiently small accuracy. When combined with previous state-of-the-art methods our result closes a gap between the best-known query depth and the best-known computational depth of parallel algorithms. Our method starts with a ball acceleration framework of previous parallel methods, i.e., [CJJJLST20, ACJJS21], which reduce the problem to minimizing a regularized Gaussian convolution of the function constrained to Euclidean balls. By developing and leveraging new stability properties of the Hessian of this induced function, we depart from prior parallel algorithms and reduce these ball-constrained optimization problems to stochastic unconstrained quadratic minimization problems. Although we are unable to prove concentration of the asymmetric matrices that we use to approximate this Hessian, we nevertheless develop an efficient parallel method for solving these quadratics. Interestingly, our algorithms can be improved using fast matrix multiplication and use nearly-linear work if the matrix multiplication exponent is 2.

Faster Spectral Density Estimation and Sparsification in the Nuclear Norm

We consider the problem of estimating the spectral density of the normalized adjacency matrix of an $n$-node undirected graph. We provide a randomized algorithm that, with $O(n\epsilon^{-2})$ queries to a degree and neighbor oracle and in $O(n\epsilon^{-3})$ time, estimates the spectrum up to $\epsilon$ accuracy in the Wasserstein-1 metric. This improves on previous state-of-the-art methods, including an $O(n\epsilon^{-7})$ time algorithm from [Braverman et al., STOC 2022] and, for sufficiently small $\epsilon$, a $2^{O(\epsilon^{-1})}$ time method from [Cohen-Steiner et al., KDD 2018]. To achieve this result, we introduce a new notion of graph sparsification, which we call nuclear sparsification. We provide an $O(n\epsilon^{-2})$-query and $O(n\epsilon^{-2})$-time algorithm for computing $O(n\epsilon^{-2})$-sparse nuclear sparsifiers. We show that this bound is optimal in both its sparsity and query complexity, and we separate our results from the related notion of additive spectral sparsification. Of independent interest, we show that our sparsification method also yields the first deterministic algorithm for spectral density estimation that scales linearly with $n$ (sublinear in the representation size of the graph).

Truncated Variance Reduced Value Iteration

We provide faster randomized algorithms for computing an $\epsilon$-optimal policy in a discounted Markov decision process with $A_{\text{tot}}$-state-action pairs, bounded rewards, and discount factor $\gamma$. We provide an $\tilde{O}(A_{\text{tot}}[(1 - \gamma)^{-3}\epsilon^{-2} + (1 - \gamma)^{-2}])$-time algorithm in the sampling setting, where the probability transition matrix is unknown but accessible through a generative model which can be queried in $\tilde{O}(1)$-time, and an $\tilde{O}(s + (1-\gamma)^{-2})$-time algorithm in the offline setting where the probability transition matrix is known and $s$-sparse. These results improve upon the prior state-of-the-art which either ran in $\tilde{O}(A_{\text{tot}}[(1 - \gamma)^{-3}\epsilon^{-2} + (1 - \gamma)^{-3}])$ time [Sidford, Wang, Wu, Ye 2018] in the sampling setting, $\tilde{O}(s + A_{\text{tot}} (1-\gamma)^{-3})$ time [Sidford, Wang, Wu, Yang, Ye 2018] in the offline setting, or time at least quadratic in the number of states using interior point methods for linear programming. We achieve our results by building upon prior stochastic variance-reduced value iteration methods [Sidford, Wang, Wu, Yang, Ye 2018]. We provide a variant that carefully truncates the progress of its iterates to improve the variance of new variance-reduced sampling procedures that we introduce to implement the steps. Our method is essentially model-free and can be implemented in $\tilde{O}(A_{\text{tot}})$-space when given generative model access. Consequently, our results take a step in closing the sample-complexity gap between model-free and model-based methods.

A Whole New Ball Game: A Primal Accelerated Method for Matrix Games and Minimizing the Maximum of Smooth Functions

We design algorithms for minimizing $\max_{i\in[n]} f_i(x)$ over a $d$-dimensional Euclidean or simplex domain. When each $f_i$ is $1$-Lipschitz and $1$-smooth, our method computes an $\epsilon$-approximate solution using $\widetilde{O}(n \epsilon^{-1/3} + \epsilon^{-2})$ gradient and function evaluations, and $\widetilde{O}(n \epsilon^{-4/3})$ additional runtime. For large $n$, our evaluation complexity is optimal up to polylogarithmic factors. In the special case where each $f_i$ is linear -- which corresponds to finding a near-optimal primal strategy in a matrix game -- our method finds an $\epsilon$-approximate solution in runtime $\widetilde{O}(n (d/\epsilon)^{2/3} + nd + d\epsilon^{-2})$. For $n>d$ and $\epsilon=1/\sqrt{n}$ this improves over all existing first-order methods. When additionally $d = \omega(n^{8/11})$ our runtime also improves over all known interior point methods. Our algorithm combines three novel primitives: (1) A dynamic data structure which enables efficient stochastic gradient estimation in small $\ell_2$ or $\ell_1$ balls. (2) A mirror descent algorithm tailored to our data structure implementing an oracle which minimizes the objective over these balls. (3) A simple ball oracle acceleration framework suitable for non-Euclidean geometry.

Structured Semidefinite Programming for Recovering Structured Preconditioners

We develop a general framework for finding approximately-optimal preconditioners for solving linear systems. Leveraging this framework we obtain improved runtimes for fundamental preconditioning and linear system solving problems including the following. We give an algorithm which, given positive definite $\mathbf{K} \in \mathbb{R}^{d \times d}$ with $\mathrm{nnz}(\mathbf{K})$ nonzero entries, computes an $\epsilon$-optimal diagonal preconditioner in time $\widetilde{O}(\mathrm{nnz}(\mathbf{K}) \cdot \mathrm{poly}(\kappa^\star,\epsilon^{-1}))$, where $\kappa^\star$ is the optimal condition number of the rescaled matrix. We give an algorithm which, given $\mathbf{M} \in \mathbb{R}^{d \times d}$ that is either the pseudoinverse of a graph Laplacian matrix or a constant spectral approximation of one, solves linear systems in $\mathbf{M}$ in $\widetilde{O}(d^2)$ time. Our diagonal preconditioning results improve state-of-the-art runtimes of $\Omega(d^{3.5})$ attained by general-purpose semidefinite programming, and our solvers improve state-of-the-art runtimes of $\Omega(d^{\omega})$ where $\omega > 2.3$ is the current matrix multiplication constant. We attain our results via new algorithms for a class of semidefinite programs (SDPs) we call matrix-dictionary approximation SDPs, which we leverage to solve an associated problem we call matrix-dictionary recovery.

Matrix Completion in Almost-Verification Time

We give a new framework for solving the fundamental problem of low-rank matrix completion, i.e., approximating a rank-$r$ matrix $\mathbf{M} \in \mathbb{R}^{m \times n}$ (where $m \ge n$) from random observations. First, we provide an algorithm which completes $\mathbf{M}$ on $99\%$ of rows and columns under no further assumptions on $\mathbf{M}$ from $\approx mr$ samples and using $\approx mr^2$ time. Then, assuming the row and column spans of $\mathbf{M}$ satisfy additional regularity properties, we show how to boost this partial completion guarantee to a full matrix completion algorithm by aggregating solutions to regression problems involving the observations. In the well-studied setting where $\mathbf{M}$ has incoherent row and column spans, our algorithms complete $\mathbf{M}$ to high precision from $mr^{2+o(1)}$ observations in $mr^{3 + o(1)}$ time (omitting logarithmic factors in problem parameters), improving upon the prior state-of-the-art [JN15] which used $\approx mr^5$ samples and $\approx mr^7$ time. Under an assumption on the row and column spans of $\mathbf{M}$ we introduce (which is satisfied by random subspaces with high probability), our sample complexity improves to an almost information-theoretically optimal $mr^{1 + o(1)}$, and our runtime improves to $mr^{2 + o(1)}$. Our runtimes have the appealing property of matching the best known runtime to verify that a rank-$r$ decomposition $\mathbf{U}\mathbf{V}^\top$ agrees with the sampled observations. We also provide robust variants of our algorithms that, given random observations from $\mathbf{M} + \mathbf{N}$ with $\|\mathbf{N}\|_{F} \le \Delta$, complete $\mathbf{M}$ to Frobenius norm distance $\approx r^{1.5}\Delta$ in the same runtimes as the noiseless setting. Prior noisy matrix completion algorithms [CP10] only guaranteed a distance of $\approx \sqrt{n}\Delta$.

Moments, Random Walks, and Limits for Spectrum Approximation

We study lower bounds for the problem of approximating a one dimensional distribution given (noisy) measurements of its moments. We show that there are distributions on $[-1,1]$ that cannot be approximated to accuracy $\epsilon$ in Wasserstein-1 distance even if we know \emph{all} of their moments to multiplicative accuracy $(1\pm2^{-\Omega(1/\epsilon)})$; this result matches an upper bound of Kong and Valiant [Annals of Statistics, 2017]. To obtain our result, we provide a hard instance involving distributions induced by the eigenvalue spectra of carefully constructed graph adjacency matrices. Efficiently approximating such spectra in Wasserstein-1 distance is a well-studied algorithmic problem, and a recent result of Cohen-Steiner et al. [KDD 2018] gives a method based on accurately approximating spectral moments using $2^{O(1/\epsilon)}$ random walks initiated at uniformly random nodes in the graph. As a strengthening of our main result, we show that improving the dependence on $1/\epsilon$ in this result would require a new algorithmic approach. Specifically, no algorithm can compute an $\epsilon$-accurate approximation to the spectrum of a normalized graph adjacency matrix with constant probability, even when given the transcript of $2^{\Omega(1/\epsilon)}$ random walks of length $2^{\Omega(1/\epsilon)}$ started at random nodes.

ReSQueing Parallel and Private Stochastic Convex Optimization

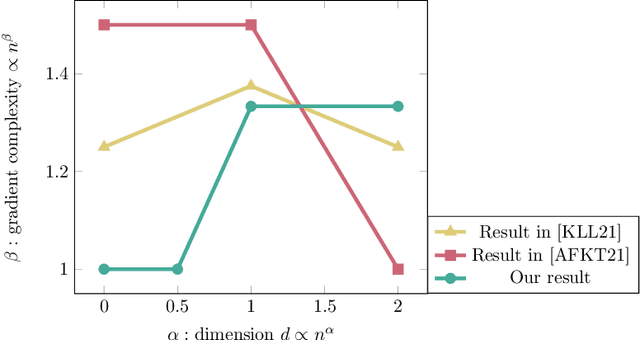
We introduce a new tool for stochastic convex optimization (SCO): a Reweighted Stochastic Query (ReSQue) estimator for the gradient of a function convolved with a (Gaussian) probability density. Combining ReSQue with recent advances in ball oracle acceleration [CJJJLST20, ACJJS21], we develop algorithms achieving state-of-the-art complexities for SCO in parallel and private settings. For a SCO objective constrained to the unit ball in $\mathbb{R}^d$, we obtain the following results (up to polylogarithmic factors). We give a parallel algorithm obtaining optimization error $\epsilon_{\text{opt}}$ with $d^{1/3}\epsilon_{\text{opt}}^{-2/3}$ gradient oracle query depth and $d^{1/3}\epsilon_{\text{opt}}^{-2/3} + \epsilon_{\text{opt}}^{-2}$ gradient queries in total, assuming access to a bounded-variance stochastic gradient estimator. For $\epsilon_{\text{opt}} \in [d^{-1}, d^{-1/4}]$, our algorithm matches the state-of-the-art oracle depth of [BJLLS19] while maintaining the optimal total work of stochastic gradient descent. We give an $(\epsilon_{\text{dp}}, \delta)$-differentially private algorithm which, given $n$ samples of Lipschitz loss functions, obtains near-optimal optimization error and makes $\min(n, n^2\epsilon_{\text{dp}}^2 d^{-1}) + \min(n^{4/3}\epsilon_{\text{dp}}^{1/3}, (nd)^{2/3}\epsilon_{\text{dp}}^{-1})$ queries to the gradients of these functions. In the regime $d \le n \epsilon_{\text{dp}}^{2}$, where privacy comes at no cost in terms of the optimal loss up to constants, our algorithm uses $n + (nd)^{2/3}\epsilon_{\text{dp}}^{-1}$ queries and improves recent advancements of [KLL21, AFKT21]. In the moderately low-dimensional setting $d \le \sqrt n \epsilon_{\text{dp}}^{3/2}$, our query complexity is near-linear.

On the Efficient Implementation of High Accuracy Optimality of Profile Maximum Likelihood

We provide an efficient unified plug-in approach for estimating symmetric properties of distributions given $n$ independent samples. Our estimator is based on profile-maximum-likelihood (PML) and is sample optimal for estimating various symmetric properties when the estimation error $\epsilon \gg n^{-1/3}$. This result improves upon the previous best accuracy threshold of $\epsilon \gg n^{-1/4}$ achievable by polynomial time computable PML-based universal estimators [ACSS21, ACSS20]. Our estimator reaches a theoretical limit for universal symmetric property estimation as [Han21] shows that a broad class of universal estimators (containing many well known approaches including ours) cannot be sample optimal for every $1$-Lipschitz property when $\epsilon \ll n^{-1/3}$.

RECAPP: Crafting a More Efficient Catalyst for Convex Optimization

The accelerated proximal point algorithm (APPA), also known as "Catalyst", is a well-established reduction from convex optimization to approximate proximal point computation (i.e., regularized minimization). This reduction is conceptually elegant and yields strong convergence rate guarantees. However, these rates feature an extraneous logarithmic term arising from the need to compute each proximal point to high accuracy. In this work, we propose a novel Relaxed Error Criterion for Accelerated Proximal Point (RECAPP) that eliminates the need for high accuracy subproblem solutions. We apply RECAPP to two canonical problems: finite-sum and max-structured minimization. For finite-sum problems, we match the best known complexity, previously obtained by carefully-designed problem-specific algorithms. For minimizing $\max_y f(x,y)$ where $f$ is convex in $x$ and strongly-concave in $y$, we improve on the best known (Catalyst-based) bound by a logarithmic factor.