A Characterization of List Language Identification in the Limit

We study the problem of language identification in the limit, where given a sequence of examples from a target language, the goal of the learner is to output a sequence of guesses for the target language such that all the guesses beyond some finite time are correct. Classical results of Gold showed that language identification in the limit is impossible for essentially any interesting collection of languages. Later, Angluin gave a precise characterization of language collections for which this task is possible. Motivated by recent positive results for the related problem of language generation, we revisit the classic language identification problem in the setting where the learner is given the additional power of producing a list of $k$ guesses at each time step. The goal is to ensure that beyond some finite time, one of the guesses is correct at each time step. We give an exact characterization of collections of languages that can be $k$-list identified in the limit, based on a recursive version of Angluin's characterization (for language identification with a list of size $1$). This further leads to a conceptually appealing characterization: A language collection can be $k$-list identified in the limit if and only if the collection can be decomposed into $k$ collections of languages, each of which can be identified in the limit (with a list of size $1$). We also use our characterization to establish rates for list identification in the statistical setting where the input is drawn as an i.i.d. stream from a distribution supported on some language in the collection. Our results show that if a collection is $k$-list identifiable in the limit, then the collection can be $k$-list identified at an exponential rate, and this is best possible. On the other hand, if a collection is not $k$-list identifiable in the limit, then it cannot be $k$-list identified at any rate that goes to zero.

Exploring Facets of Language Generation in the Limit

The recent work of Kleinberg and Mullainathan [KM24] provides a concrete model for language generation in the limit: given a sequence of examples from an unknown target language, the goal is to generate new examples from the target language such that no incorrect examples are generated beyond some point. In sharp contrast to strong negative results for the closely related problem of language identification, they establish positive results for language generation in the limit for all countable collections of languages. Follow-up work by Raman and Tewari [RT24] studies bounds on the number of distinct inputs required by an algorithm before correct language generation is achieved -- namely, whether this is a constant for all languages in the collection (uniform generation) or a language-dependent constant (non-uniform generation). We show that every countable language collection has a generator which has the stronger property of non-uniform generation in the limit. However, while the generation algorithm of [KM24] can be implemented using membership queries, we show that any algorithm cannot non-uniformly generate even for collections of just two languages, using only membership queries. We also formalize the tension between validity and breadth in the generation algorithm of [KM24] by introducing a definition of exhaustive generation, and show a strong negative result for exhaustive generation. Our result shows that a tradeoff between validity and breadth is inherent for generation in the limit. Finally, inspired by algorithms that can choose to obtain feedback, we consider a model of uniform generation with feedback, completely characterizing language collections for which such uniform generation with feedback is possible in terms of a complexity measure of the collection.

Quantifying the Gain in Weak-to-Strong Generalization

Recent advances in large language models have shown capabilities that are extraordinary and near-superhuman. These models operate with such complexity that reliably evaluating and aligning them proves challenging for humans. This leads to the natural question: can guidance from weak models (like humans) adequately direct the capabilities of strong models? In a recent and somewhat surprising work, Burns et al. (2023) empirically demonstrated that when strong models (like GPT-4) are finetuned using labels generated by weak supervisors (like GPT-2), the strong models outperform their weaker counterparts -- a phenomenon they term weak-to-strong generalization. In this work, we present a theoretical framework for understanding weak-to-strong generalization. Specifically, we show that the improvement in performance achieved by strong models over their weaker counterparts is quantified by the misfit error incurred by the strong model on labels generated by the weaker model. Our theory reveals several curious algorithmic insights. For instance, we can predict the amount by which the strong model will improve over the weak model, and also choose among different weak models to train the strong model, based on its misfit error. We validate our theoretical findings through various empirical assessments.

Dynamic Data Layout Optimization with Worst-case Guarantees

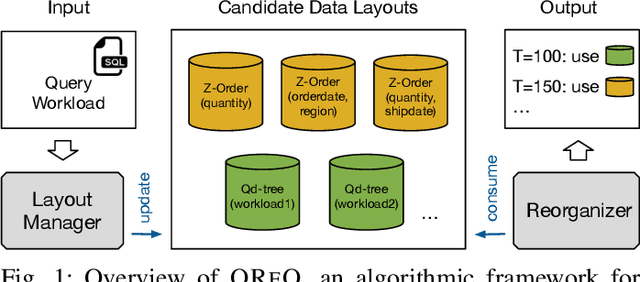
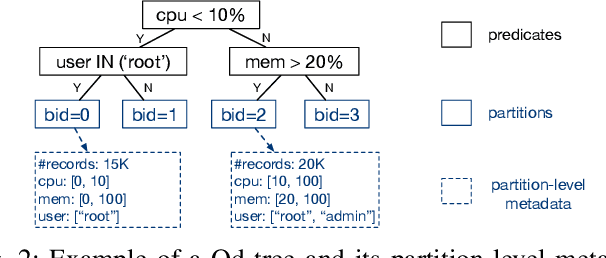
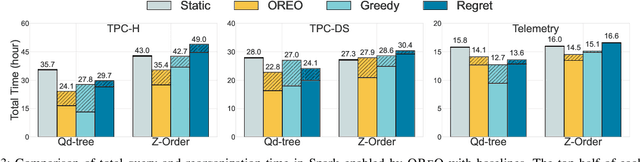
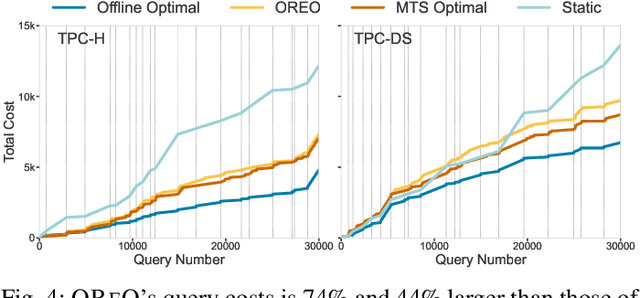
Many data analytics systems store and process large datasets in partitions containing millions of rows. By mapping rows to partitions in an optimized way, it is possible to improve query performance by skipping over large numbers of irrelevant partitions during query processing. This mapping is referred to as a data layout. Recent works have shown that customizing the data layout to the anticipated query workload greatly improves query performance, but the performance benefits may disappear if the workload changes. Reorganizing data layouts to accommodate workload drift can resolve this issue, but reorganization costs could exceed query savings if not done carefully. In this paper, we present an algorithmic framework OReO that makes online reorganization decisions to balance the benefits of improved query performance with the costs of reorganization. Our framework extends results from Metrical Task Systems to provide a tight bound on the worst-case performance guarantee for online reorganization, without prior knowledge of the query workload. Through evaluation on real-world datasets and query workloads, our experiments demonstrate that online reorganization with OReO can lead to an up to 32% improvement in combined query and reorganization time compared to using a single, optimized data layout for the entire workload.

Simple, Scalable and Effective Clustering via One-Dimensional Projections

Clustering is a fundamental problem in unsupervised machine learning with many applications in data analysis. Popular clustering algorithms such as Lloyd's algorithm and $k$-means++ can take $\Omega(ndk)$ time when clustering $n$ points in a $d$-dimensional space (represented by an $n\times d$ matrix $X$) into $k$ clusters. In applications with moderate to large $k$, the multiplicative $k$ factor can become very expensive. We introduce a simple randomized clustering algorithm that provably runs in expected time $O(\mathrm{nnz}(X) + n\log n)$ for arbitrary $k$. Here $\mathrm{nnz}(X)$ is the total number of non-zero entries in the input dataset $X$, which is upper bounded by $nd$ and can be significantly smaller for sparse datasets. We prove that our algorithm achieves approximation ratio $\smash{\widetilde{O}(k^4)}$ on any input dataset for the $k$-means objective. We also believe that our theoretical analysis is of independent interest, as we show that the approximation ratio of a $k$-means algorithm is approximately preserved under a class of projections and that $k$-means++ seeding can be implemented in expected $O(n \log n)$ time in one dimension. Finally, we show experimentally that our clustering algorithm gives a new tradeoff between running time and cluster quality compared to previous state-of-the-art methods for these tasks.

Breaking the Metric Voting Distortion Barrier

We consider the following well studied problem of metric distortion in social choice. Suppose we have an election with $n$ voters and $m$ candidates who lie in a shared metric space. We would like to design a voting rule that chooses a candidate whose average distance to the voters is small. However, instead of having direct access to the distances in the metric space, each voter gives us a ranked list of the candidates in order of distance. Can we design a rule that regardless of the election instance and underlying metric space, chooses a candidate whose cost differs from the true optimum by only a small factor (known as the distortion)? A long line of work culminated in finding deterministic voting rules with metric distortion $3$, which is the best possible for deterministic rules and many other classes of voting rules. However, without any restrictions, there is still a significant gap in our understanding: Even though the best lower bound is substantially lower at $2.112$, the best upper bound is still $3$, which is attained even by simple rules such as Random Dictatorship. Finding a rule that guarantees distortion $3 - \varepsilon$ for some constant $\varepsilon $ has been a major challenge in computational social choice. In this work, we give a rule that guarantees distortion less than $2.753$. To do so we study a handful of voting rules that are new to the problem. One is Maximal Lotteries, a rule based on the Nash equilibrium of a natural zero-sum game which dates back to the 60's. The others are novel rules that can be thought of as hybrids of Random Dictatorship and the Copeland rule. Though none of these rules can beat distortion $3$ alone, a careful randomization between Maximal Lotteries and any of the novel rules can.

A Characterization of List Learnability

A classical result in learning theory shows the equivalence of PAC learnability of binary hypothesis classes and the finiteness of VC dimension. Extending this to the multiclass setting was an open problem, which was settled in a recent breakthrough result characterizing multiclass PAC learnability via the DS dimension introduced earlier by Daniely and Shalev-Shwartz. In this work we consider list PAC learning where the goal is to output a list of $k$ predictions. List learning algorithms have been developed in several settings before and indeed, list learning played an important role in the recent characterization of multiclass learnability. In this work we ask: when is it possible to $k$-list learn a hypothesis class? We completely characterize $k$-list learnability in terms of a generalization of DS dimension that we call the $k$-DS dimension. Generalizing the recent characterization of multiclass learnability, we show that a hypothesis class is $k$-list learnable if and only if the $k$-DS dimension is finite.

On the Efficient Implementation of High Accuracy Optimality of Profile Maximum Likelihood

We provide an efficient unified plug-in approach for estimating symmetric properties of distributions given $n$ independent samples. Our estimator is based on profile-maximum-likelihood (PML) and is sample optimal for estimating various symmetric properties when the estimation error $\epsilon \gg n^{-1/3}$. This result improves upon the previous best accuracy threshold of $\epsilon \gg n^{-1/4}$ achievable by polynomial time computable PML-based universal estimators [ACSS21, ACSS20]. Our estimator reaches a theoretical limit for universal symmetric property estimation as [Han21] shows that a broad class of universal estimators (containing many well known approaches including ours) cannot be sample optimal for every $1$-Lipschitz property when $\epsilon \ll n^{-1/3}$.

Near-Optimal Explainable $k$-Means for All Dimensions

Many clustering algorithms are guided by certain cost functions such as the widely-used $k$-means cost. These algorithms divide data points into clusters with often complicated boundaries, creating difficulties in explaining the clustering decision. In a recent work, Dasgupta, Frost, Moshkovitz, and Rashtchian (ICML'20) introduced explainable clustering, where the cluster boundaries are axis-parallel hyperplanes and the clustering is obtained by applying a decision tree to the data. The central question here is: how much does the explainability constraint increase the value of the cost function? Given $d$-dimensional data points, we show an efficient algorithm that finds an explainable clustering whose $k$-means cost is at most $k^{1 - 2/d}\mathrm{poly}(d\log k)$ times the minimum cost achievable by a clustering without the explainability constraint, assuming $k,d\ge 2$. Combining this with an independent work by Makarychev and Shan (ICML'21), we get an improved bound of $k^{1 - 2/d}\mathrm{polylog}(k)$, which we show is optimal for every choice of $k,d\ge 2$ up to a poly-logarithmic factor in $k$. For $d = 2$ in particular, we show an $O(\log k\log\log k)$ bound, improving exponentially over the previous best bound of $\widetilde O(k)$.

Instance Based Approximations to Profile Maximum Likelihood

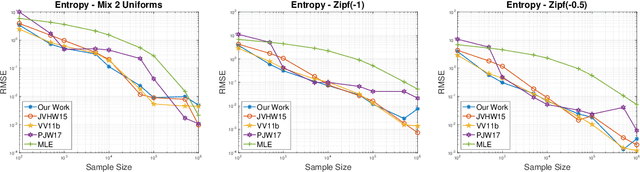
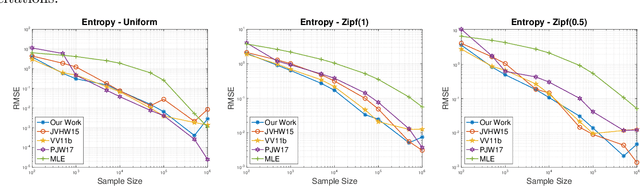
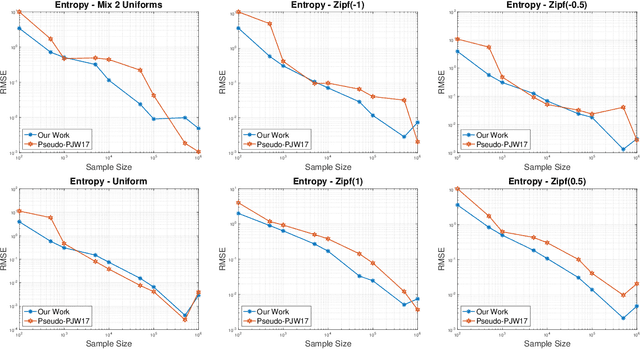
In this paper we provide a new efficient algorithm for approximately computing the profile maximum likelihood (PML) distribution, a prominent quantity in symmetric property estimation. We provide an algorithm which matches the previous best known efficient algorithms for computing approximate PML distributions and improves when the number of distinct observed frequencies in the given instance is small. We achieve this result by exploiting new sparsity structure in approximate PML distributions and providing a new matrix rounding algorithm, of independent interest. Leveraging this result, we obtain the first provable computationally efficient implementation of PseudoPML, a general framework for estimating a broad class of symmetric properties. Additionally, we obtain efficient PML-based estimators for distributions with small profile entropy, a natural instance-based complexity measure. Further, we provide a simpler and more practical PseudoPML implementation that matches the best-known theoretical guarantees of such an estimator and evaluate this method empirically.