Parallel Sampling via Counting

We show how to use parallelization to speed up sampling from an arbitrary distribution $\mu$ on a product space $[q]^n$, given oracle access to counting queries: $\mathbb{P}_{X\sim \mu}[X_S=\sigma_S]$ for any $S\subseteq [n]$ and $\sigma_S \in [q]^S$. Our algorithm takes $O({n^{2/3}\cdot \operatorname{polylog}(n,q)})$ parallel time, to the best of our knowledge, the first sublinear in $n$ runtime for arbitrary distributions. Our results have implications for sampling in autoregressive models. Our algorithm directly works with an equivalent oracle that answers conditional marginal queries $\mathbb{P}_{X\sim \mu}[X_i=\sigma_i\;\vert\; X_S=\sigma_S]$, whose role is played by a trained neural network in autoregressive models. This suggests a roughly $n^{1/3}$-factor speedup is possible for sampling in any-order autoregressive models. We complement our positive result by showing a lower bound of $\widetilde{\Omega}(n^{1/3})$ for the runtime of any parallel sampling algorithm making at most $\operatorname{poly}(n)$ queries to the counting oracle, even for $q=2$.

Batch Active Learning of Reward Functions from Human Preferences

Data generation and labeling are often expensive in robot learning. Preference-based learning is a concept that enables reliable labeling by querying users with preference questions. Active querying methods are commonly employed in preference-based learning to generate more informative data at the expense of parallelization and computation time. In this paper, we develop a set of novel algorithms, batch active preference-based learning methods, that enable efficient learning of reward functions using as few data samples as possible while still having short query generation times and also retaining parallelizability. We introduce a method based on determinantal point processes (DPP) for active batch generation and several heuristic-based alternatives. Finally, we present our experimental results for a variety of robotics tasks in simulation. Our results suggest that our batch active learning algorithm requires only a few queries that are computed in a short amount of time. We showcase one of our algorithms in a study to learn human users' preferences.

Fast parallel sampling under isoperimetry

We show how to sample in parallel from a distribution $\pi$ over $\mathbb R^d$ that satisfies a log-Sobolev inequality and has a smooth log-density, by parallelizing the Langevin (resp. underdamped Langevin) algorithms. We show that our algorithm outputs samples from a distribution $\hat\pi$ that is close to $\pi$ in Kullback--Leibler (KL) divergence (resp. total variation (TV) distance), while using only $\log(d)^{O(1)}$ parallel rounds and $\widetilde{O}(d)$ (resp. $\widetilde O(\sqrt d)$) gradient evaluations in total. This constitutes the first parallel sampling algorithms with TV distance guarantees. For our main application, we show how to combine the TV distance guarantees of our algorithms with prior works and obtain RNC sampling-to-counting reductions for families of discrete distribution on the hypercube $\{\pm 1\}^n$ that are closed under exponential tilts and have bounded covariance. Consequently, we obtain an RNC sampler for directed Eulerian tours and asymmetric determinantal point processes, resolving open questions raised in prior works.

Parallel Sampling of Diffusion Models

Diffusion models are powerful generative models but suffer from slow sampling, often taking 1000 sequential denoising steps for one sample. As a result, considerable efforts have been directed toward reducing the number of denoising steps, but these methods hurt sample quality. Instead of reducing the number of denoising steps (trading quality for speed), in this paper we explore an orthogonal approach: can we run the denoising steps in parallel (trading compute for speed)? In spite of the sequential nature of the denoising steps, we show that surprisingly it is possible to parallelize sampling via Picard iterations, by guessing the solution of future denoising steps and iteratively refining until convergence. With this insight, we present ParaDiGMS, a novel method to accelerate the sampling of pretrained diffusion models by denoising multiple steps in parallel. ParaDiGMS is the first diffusion sampling method that enables trading compute for speed and is even compatible with existing fast sampling techniques such as DDIM and DPMSolver. Using ParaDiGMS, we improve sampling speed by 2-4x across a range of robotics and image generation models, giving state-of-the-art sampling speeds of 0.2s on 100-step DiffusionPolicy and 16s on 1000-step StableDiffusion-v2 with no measurable degradation of task reward, FID score, or CLIP score.

Optimal Sublinear Sampling of Spanning Trees and Determinantal Point Processes via Average-Case Entropic Independence

We design fast algorithms for repeatedly sampling from strongly Rayleigh distributions, which include random spanning tree distributions and determinantal point processes. For a graph $G=(V, E)$, we show how to approximately sample uniformly random spanning trees from $G$ in $\widetilde{O}(\lvert V\rvert)$ time per sample after an initial $\widetilde{O}(\lvert E\rvert)$ time preprocessing. For a determinantal point process on subsets of size $k$ of a ground set of $n$ elements, we show how to approximately sample in $\widetilde{O}(k^\omega)$ time after an initial $\widetilde{O}(nk^{\omega-1})$ time preprocessing, where $\omega<2.372864$ is the matrix multiplication exponent. We even improve the state of the art for obtaining a single sample from determinantal point processes, from the prior runtime of $\widetilde{O}(\min\{nk^2, n^\omega\})$ to $\widetilde{O}(nk^{\omega-1})$. In our main technical result, we achieve the optimal limit on domain sparsification for strongly Rayleigh distributions. In domain sparsification, sampling from a distribution $\mu$ on $\binom{[n]}{k}$ is reduced to sampling from related distributions on $\binom{[t]}{k}$ for $t\ll n$. We show that for strongly Rayleigh distributions, we can can achieve the optimal $t=\widetilde{O}(k)$. Our reduction involves sampling from $\widetilde{O}(1)$ domain-sparsified distributions, all of which can be produced efficiently assuming convenient access to approximate overestimates for marginals of $\mu$. Having access to marginals is analogous to having access to the mean and covariance of a continuous distribution, or knowing "isotropy" for the distribution, the key assumption behind the Kannan-Lov\'asz-Simonovits (KLS) conjecture and optimal samplers based on it. We view our result as a moral analog of the KLS conjecture and its consequences for sampling, for discrete strongly Rayleigh measures.

Learning Multimodal Rewards from Rankings

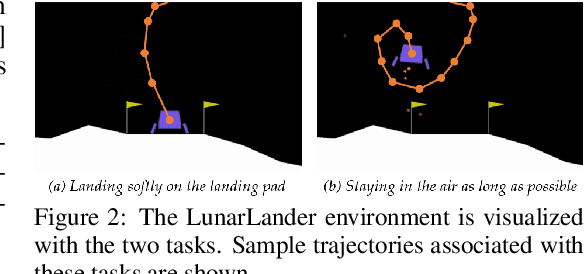
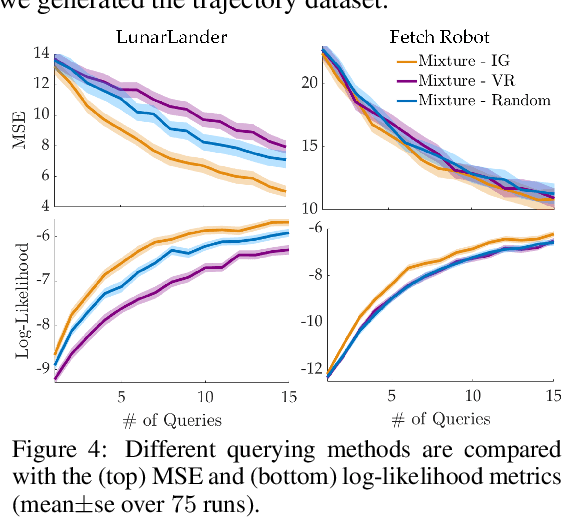
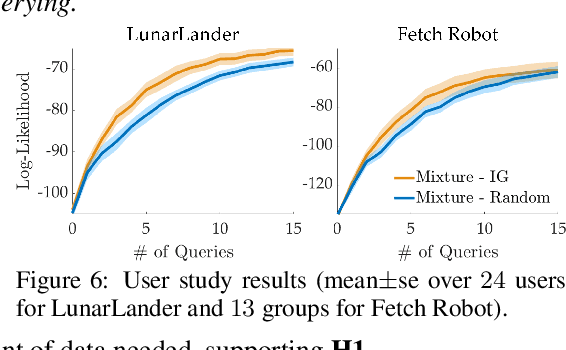
Learning from human feedback has shown to be a useful approach in acquiring robot reward functions. However, expert feedback is often assumed to be drawn from an underlying unimodal reward function. This assumption does not always hold including in settings where multiple experts provide data or when a single expert provides data for different tasks -- we thus go beyond learning a unimodal reward and focus on learning a multimodal reward function. We formulate the multimodal reward learning as a mixture learning problem and develop a novel ranking-based learning approach, where the experts are only required to rank a given set of trajectories. Furthermore, as access to interaction data is often expensive in robotics, we develop an active querying approach to accelerate the learning process. We conduct experiments and user studies using a multi-task variant of OpenAI's LunarLander and a real Fetch robot, where we collect data from multiple users with different preferences. The results suggest that our approach can efficiently learn multimodal reward functions, and improve data-efficiency over benchmark methods that we adapt to our learning problem.

Simple and Near-Optimal MAP Inference for Nonsymmetric DPPs

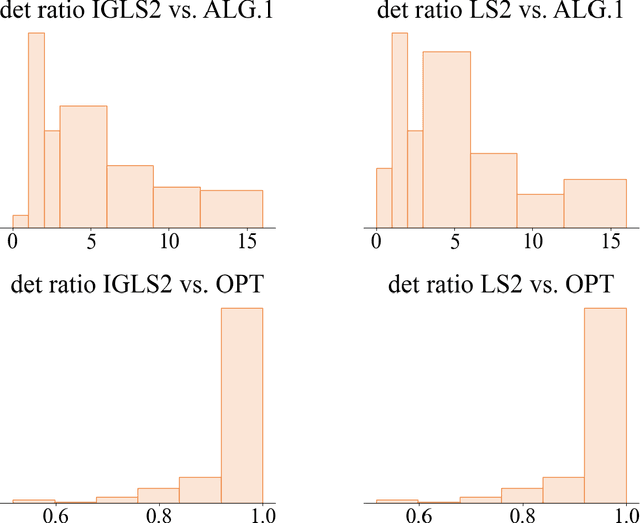
Determinantal point processes (DPPs) are widely popular probabilistic models used in machine learning to capture diversity in random subsets of items. While traditional DPPs are defined by a symmetric kernel matrix, recent work has shown a significant increase in the modeling power and applicability of models defined by nonsymmetric kernels, where the model can capture interactions that go beyond diversity. We study the problem of maximum a posteriori (MAP) inference for determinantal point processes defined by a nonsymmetric positive semidefinite matrix (NDPPs), where the goal is to find the maximum $k\times k$ principal minor of the kernel matrix $L$. We obtain the first multiplicative approximation guarantee for this problem using local search, a method that has been previously applied to symmetric DPPs. Our approximation factor of $k^{O(k)}$ is nearly tight, and we show theoretically and experimentally that it compares favorably to the state-of-the-art methods for this problem that are based on greedy maximization. The main new insight enabling our improved approximation factor is that we allow local search to update up to two elements of the solution in each iteration, and we show this is necessary to have any multiplicative approximation guarantee.

Instance Based Approximations to Profile Maximum Likelihood

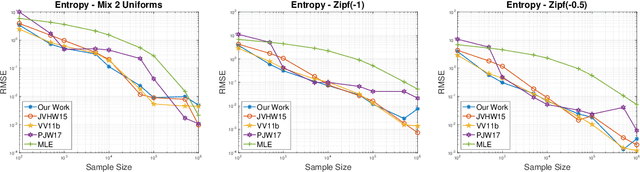
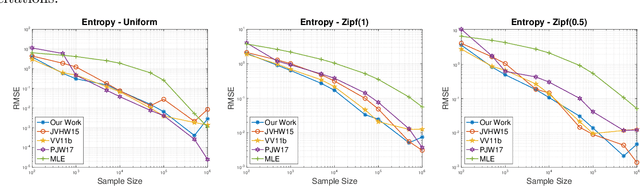
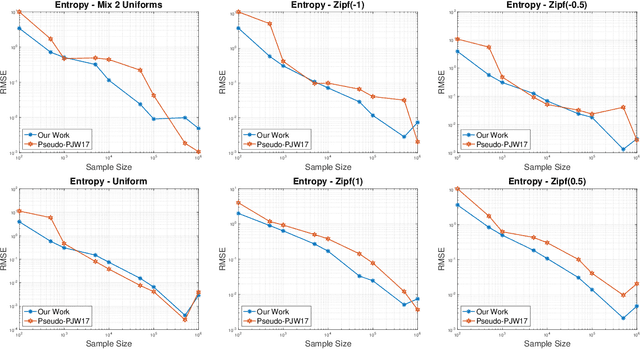
In this paper we provide a new efficient algorithm for approximately computing the profile maximum likelihood (PML) distribution, a prominent quantity in symmetric property estimation. We provide an algorithm which matches the previous best known efficient algorithms for computing approximate PML distributions and improves when the number of distinct observed frequencies in the given instance is small. We achieve this result by exploiting new sparsity structure in approximate PML distributions and providing a new matrix rounding algorithm, of independent interest. Leveraging this result, we obtain the first provable computationally efficient implementation of PseudoPML, a general framework for estimating a broad class of symmetric properties. Additionally, we obtain efficient PML-based estimators for distributions with small profile entropy, a natural instance-based complexity measure. Further, we provide a simpler and more practical PseudoPML implementation that matches the best-known theoretical guarantees of such an estimator and evaluate this method empirically.

The Bethe and Sinkhorn Permanents of Low Rank Matrices and Implications for Profile Maximum Likelihood

In this paper we consider the problem of computing the likelihood of the profile of a discrete distribution, i.e., the probability of observing the multiset of element frequencies, and computing a profile maximum likelihood (PML) distribution, i.e., a distribution with the maximum profile likelihood. For each problem we provide polynomial time algorithms that given $n$ i.i.d.\ samples from a discrete distribution, achieve an approximation factor of $\exp\left(-O(\sqrt{n} \log n) \right)$, improving upon the previous best-known bound achievable in polynomial time of $\exp(-O(n^{2/3} \log n))$ (Charikar, Shiragur and Sidford, 2019). Through the work of Acharya, Das, Orlitsky and Suresh (2016), this implies a polynomial time universal estimator for symmetric properties of discrete distributions in a broader range of error parameter. We achieve these results by providing new bounds on the quality of approximation of the Bethe and Sinkhorn permanents (Vontobel, 2012 and 2014). We show that each of these are $\exp(O(k \log(N/k)))$ approximations to the permanent of $N \times N$ matrices with non-negative rank at most $k$, improving upon the previous known bounds of $\exp(O(N))$. To obtain our results on PML, we exploit the fact that the PML objective is proportional to the permanent of a certain Vandermonde matrix with $\sqrt{n}$ distinct columns, i.e. with non-negative rank at most $\sqrt{n}$. As a by-product of our work we establish a surprising connection between the convex relaxation in prior work (CSS19) and the well-studied Bethe and Sinkhorn approximations.

Batch Active Learning Using Determinantal Point Processes

Data collection and labeling is one of the main challenges in employing machine learning algorithms in a variety of real-world applications with limited data. While active learning methods attempt to tackle this issue by labeling only the data samples that give high information, they generally suffer from large computational costs and are impractical in settings where data can be collected in parallel. Batch active learning methods attempt to overcome this computational burden by querying batches of samples at a time. To avoid redundancy between samples, previous works rely on some ad hoc combination of sample quality and diversity. In this paper, we present a new principled batch active learning method using Determinantal Point Processes, a repulsive point process that enables generating diverse batches of samples. We develop tractable algorithms to approximate the mode of a DPP distribution, and provide theoretical guarantees on the degree of approximation. We further demonstrate that an iterative greedy method for DPP maximization, which has lower computational costs but worse theoretical guarantees, still gives competitive results for batch active learning. Our experiments show the value of our methods on several datasets against state-of-the-art baselines.