Parallel Sampling via Counting

We show how to use parallelization to speed up sampling from an arbitrary distribution $\mu$ on a product space $[q]^n$, given oracle access to counting queries: $\mathbb{P}_{X\sim \mu}[X_S=\sigma_S]$ for any $S\subseteq [n]$ and $\sigma_S \in [q]^S$. Our algorithm takes $O({n^{2/3}\cdot \operatorname{polylog}(n,q)})$ parallel time, to the best of our knowledge, the first sublinear in $n$ runtime for arbitrary distributions. Our results have implications for sampling in autoregressive models. Our algorithm directly works with an equivalent oracle that answers conditional marginal queries $\mathbb{P}_{X\sim \mu}[X_i=\sigma_i\;\vert\; X_S=\sigma_S]$, whose role is played by a trained neural network in autoregressive models. This suggests a roughly $n^{1/3}$-factor speedup is possible for sampling in any-order autoregressive models. We complement our positive result by showing a lower bound of $\widetilde{\Omega}(n^{1/3})$ for the runtime of any parallel sampling algorithm making at most $\operatorname{poly}(n)$ queries to the counting oracle, even for $q=2$.

The complexity of approximate (coarse) correlated equilibrium for incomplete information games

We study the iteration complexity of decentralized learning of approximate correlated equilibria in incomplete information games. On the negative side, we prove that in $\mathit{extensive}$-$\mathit{form}$ $\mathit{games}$, assuming $\mathsf{PPAD} \not\subset \mathsf{TIME}(n^{\mathsf{polylog}(n)})$, any polynomial-time learning algorithms must take at least $2^{\log_2^{1-o(1)}(|\mathcal{I}|)}$ iterations to converge to the set of $\epsilon$-approximate correlated equilibrium, where $|\mathcal{I}|$ is the number of nodes in the game and $\epsilon > 0$ is an absolute constant. This nearly matches, up to the $o(1)$ term, the algorithms of [PR'24, DDFG'24] for learning $\epsilon$-approximate correlated equilibrium, and resolves an open question of Anagnostides, Kalavasis, Sandholm, and Zampetakis [AKSZ'24]. Our lower bound holds even for the easier solution concept of $\epsilon$-approximate $\mathit{coarse}$ correlated equilibrium On the positive side, we give uncoupled dynamics that reach $\epsilon$-approximate correlated equilibria of a $\mathit{Bayesian}$ $\mathit{game}$ in polylogarithmic iterations, without any dependence of the number of types. This demonstrates a separation between Bayesian games and extensive-form games.

Strategizing against No-Regret Learners in First-Price Auctions

We study repeated first-price auctions and general repeated Bayesian games between two players, where one player, the learner, employs a no-regret learning algorithm, and the other player, the optimizer, knowing the learner's algorithm, strategizes to maximize its own utility. For a commonly used class of no-regret learning algorithms called mean-based algorithms, we show that (i) in standard (i.e., full-information) first-price auctions, the optimizer cannot get more than the Stackelberg utility -- a standard benchmark in the literature, but (ii) in Bayesian first-price auctions, there are instances where the optimizer can achieve much higher than the Stackelberg utility. On the other hand, Mansour et al. (2022) showed that a more sophisticated class of algorithms called no-polytope-swap-regret algorithms are sufficient to cap the optimizer's utility at the Stackelberg utility in any repeated Bayesian game (including Bayesian first-price auctions), and they pose the open question whether no-polytope-swap-regret algorithms are necessary to cap the optimizer's utility. For general Bayesian games, under a reasonable and necessary condition, we prove that no-polytope-swap-regret algorithms are indeed necessary to cap the optimizer's utility and thus answer their open question. For Bayesian first-price auctions, we give a simple improvement of the standard algorithm for minimizing the polytope swap regret by exploiting the structure of Bayesian first-price auctions.

Fast swap regret minimization and applications to approximate correlated equilibria

We give a simple and computationally efficient algorithm that, for any constant $\varepsilon>0$, obtains $\varepsilon T$-swap regret within only $T = \mathsf{polylog}(n)$ rounds; this is an exponential improvement compared to the super-linear number of rounds required by the state-of-the-art algorithm, and resolves the main open problem of [Blum and Mansour 2007]. Our algorithm has an exponential dependence on $\varepsilon$, but we prove a new, matching lower bound. Our algorithm for swap regret implies faster convergence to $\varepsilon$-Correlated Equilibrium ($\varepsilon$-CE) in several regimes: For normal form two-player games with $n$ actions, it implies the first uncoupled dynamics that converges to the set of $\varepsilon$-CE in polylogarithmic rounds; a $\mathsf{polylog}(n)$-bit communication protocol for $\varepsilon$-CE in two-player games (resolving an open problem mentioned by [Babichenko-Rubinstein'2017, Goos-Rubinstein'2018, Ganor-CS'2018]; and an $\tilde{O}(n)$-query algorithm for $\varepsilon$-CE (resolving an open problem of [Babichenko'2020] and obtaining the first separation between $\varepsilon$-CE and $\varepsilon$-Nash equilibrium in the query complexity model). For extensive-form games, our algorithm implies a PTAS for $\mathit{normal}$ $\mathit{form}$ $\mathit{correlated}$ $\mathit{equilibria}$, a solution concept often conjectured to be computationally intractable (e.g. [Stengel-Forges'08, Fujii'23]).

Near Optimal Memory-Regret Tradeoff for Online Learning

In the experts problem, on each of $T$ days, an agent needs to follow the advice of one of $n$ ``experts''. After each day, the loss associated with each expert's advice is revealed. A fundamental result in learning theory says that the agent can achieve vanishing regret, i.e. their cumulative loss is within $o(T)$ of the cumulative loss of the best-in-hindsight expert. Can the agent perform well without sufficient space to remember all the experts? We extend a nascent line of research on this question in two directions: $\bullet$ We give a new algorithm against the oblivious adversary, improving over the memory-regret tradeoff obtained by [PZ23], and nearly matching the lower bound of [SWXZ22]. $\bullet$ We also consider an adaptive adversary who can observe past experts chosen by the agent. In this setting we give both a new algorithm and a novel lower bound, proving that roughly $\sqrt{n}$ memory is both necessary and sufficient for obtaining $o(T)$ regret.

The Limitations of Optimization from Samples

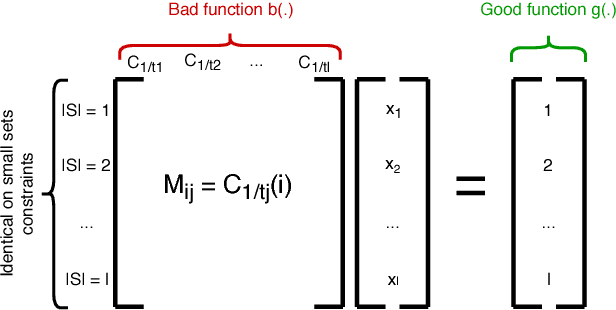
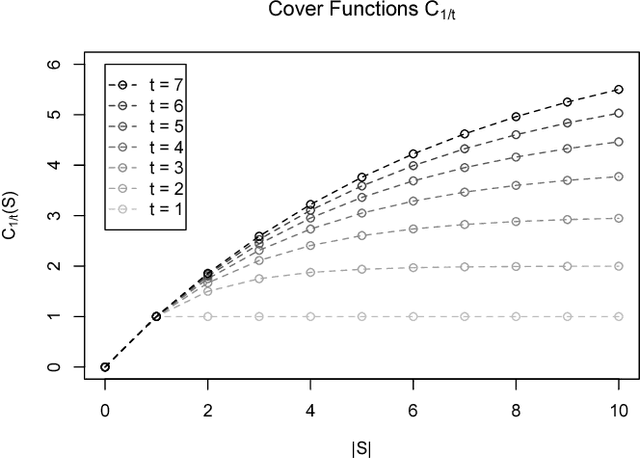
In this paper we consider the following question: can we optimize objective functions from the training data we use to learn them? We formalize this question through a novel framework we call optimization from samples (OPS). In OPS, we are given sampled values of a function drawn from some distribution and the objective is to optimize the function under some constraint. While there are interesting classes of functions that can be optimized from samples, our main result is an impossibility. We show that there are classes of functions which are statistically learnable and optimizable, but for which no reasonable approximation for optimization from samples is achievable. In particular, our main result shows that there is no constant factor approximation for maximizing coverage functions under a cardinality constraint using polynomially-many samples drawn from any distribution. We also show tight approximation guarantees for maximization under a cardinality constraint of several interesting classes of functions including unit-demand, additive, and general monotone submodular functions, as well as a constant factor approximation for monotone submodular functions with bounded curvature.

On the Worst-Case Approximability of Sparse PCA

It is well known that Sparse PCA (Sparse Principal Component Analysis) is NP-hard to solve exactly on worst-case instances. What is the complexity of solving Sparse PCA approximately? Our contributions include: 1) a simple and efficient algorithm that achieves an $n^{-1/3}$-approximation; 2) NP-hardness of approximation to within $(1-\varepsilon)$, for some small constant $\varepsilon > 0$; 3) SSE-hardness of approximation to within any constant factor; and 4) an $\exp\exp\left(\Omega\left(\sqrt{\log \log n}\right)\right)$ ("quasi-quasi-polynomial") gap for the standard semidefinite program.