UniSearch: Rethinking Search System with a Unified Generative Architecture

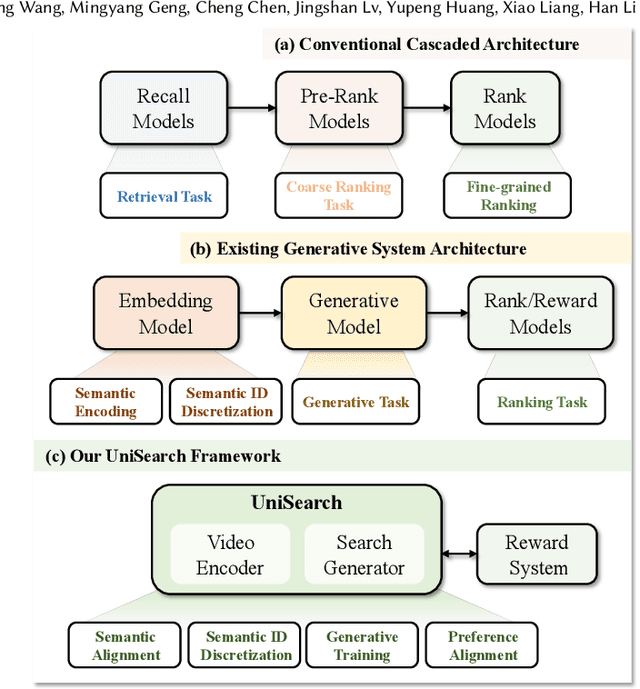
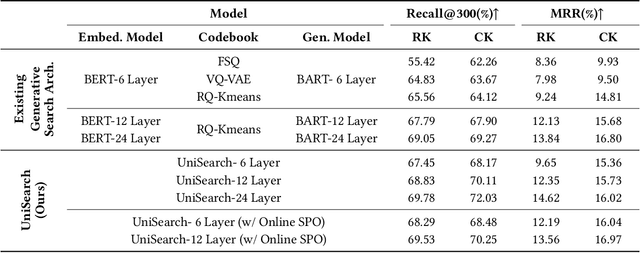
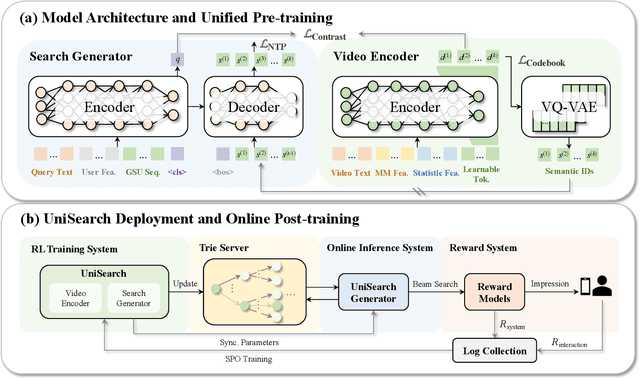
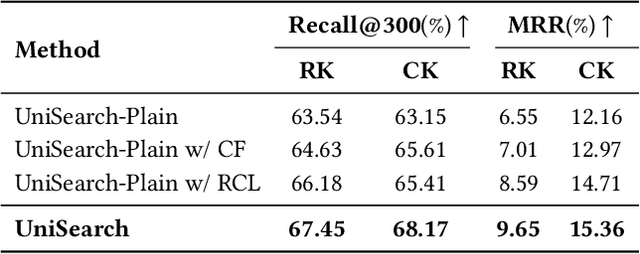
Modern search systems play a crucial role in facilitating information acquisition. Traditional search engines typically rely on a cascaded architecture, where results are retrieved through recall, pre-ranking, and ranking stages. The complexity of designing and maintaining multiple modules makes it difficult to achieve holistic performance gains. Recent advances in generative recommendation have motivated the exploration of unified generative search as an alternative. However, existing approaches are not genuinely end-to-end: they typically train an item encoder to tokenize candidates first and then optimize a generator separately, leading to objective inconsistency and limited generalization. To address these limitations, we propose UniSearch, a unified generative search framework for Kuaishou Search. UniSearch replaces the cascaded pipeline with an end-to-end architecture that integrates a Search Generator and a Video Encoder. The Generator produces semantic identifiers of relevant items given a user query, while the Video Encoder learns latent item embeddings and provides their tokenized representations. A unified training framework jointly optimizes both components, enabling mutual enhancement and improving representation quality and generation accuracy. Furthermore, we introduce Search Preference Optimization (SPO), which leverages a reward model and real user feedback to better align generation with user preferences. Extensive experiments on industrial-scale datasets, together with online A/B testing in both short-video and live search scenarios, demonstrate the strong effectiveness and deployment potential of UniSearch. Notably, its deployment in live search yields the largest single-experiment improvement in recent years of our product's history, highlighting its practical value for real-world applications.

Spot Risks Before Speaking! Unraveling Safety Attention Heads in Large Vision-Language Models

With the integration of an additional modality, large vision-language models (LVLMs) exhibit greater vulnerability to safety risks (e.g., jailbreaking) compared to their language-only predecessors. Although recent studies have devoted considerable effort to the post-hoc alignment of LVLMs, the inner safety mechanisms remain largely unexplored. In this paper, we discover that internal activations of LVLMs during the first token generation can effectively identify malicious prompts across different attacks. This inherent safety perception is governed by sparse attention heads, which we term ``safety heads." Further analysis reveals that these heads act as specialized shields against malicious prompts; ablating them leads to higher attack success rates, while the model's utility remains unaffected. By locating these safety heads and concatenating their activations, we construct a straightforward but powerful malicious prompt detector that integrates seamlessly into the generation process with minimal extra inference overhead. Despite its simple structure of a logistic regression model, the detector surprisingly exhibits strong zero-shot generalization capabilities. Experiments across various prompt-based attacks confirm the effectiveness of leveraging safety heads to protect LVLMs. Code is available at \url{https://github.com/Ziwei-Zheng/SAHs}.

Strategizing against No-Regret Learners in First-Price Auctions

We study repeated first-price auctions and general repeated Bayesian games between two players, where one player, the learner, employs a no-regret learning algorithm, and the other player, the optimizer, knowing the learner's algorithm, strategizes to maximize its own utility. For a commonly used class of no-regret learning algorithms called mean-based algorithms, we show that (i) in standard (i.e., full-information) first-price auctions, the optimizer cannot get more than the Stackelberg utility -- a standard benchmark in the literature, but (ii) in Bayesian first-price auctions, there are instances where the optimizer can achieve much higher than the Stackelberg utility. On the other hand, Mansour et al. (2022) showed that a more sophisticated class of algorithms called no-polytope-swap-regret algorithms are sufficient to cap the optimizer's utility at the Stackelberg utility in any repeated Bayesian game (including Bayesian first-price auctions), and they pose the open question whether no-polytope-swap-regret algorithms are necessary to cap the optimizer's utility. For general Bayesian games, under a reasonable and necessary condition, we prove that no-polytope-swap-regret algorithms are indeed necessary to cap the optimizer's utility and thus answer their open question. For Bayesian first-price auctions, we give a simple improvement of the standard algorithm for minimizing the polytope swap regret by exploiting the structure of Bayesian first-price auctions.

Robust Maximization of Non-Submodular Objectives

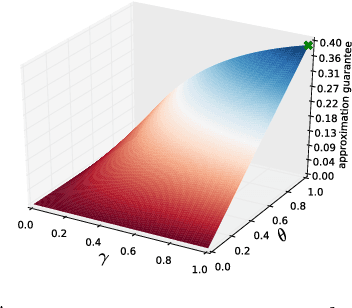
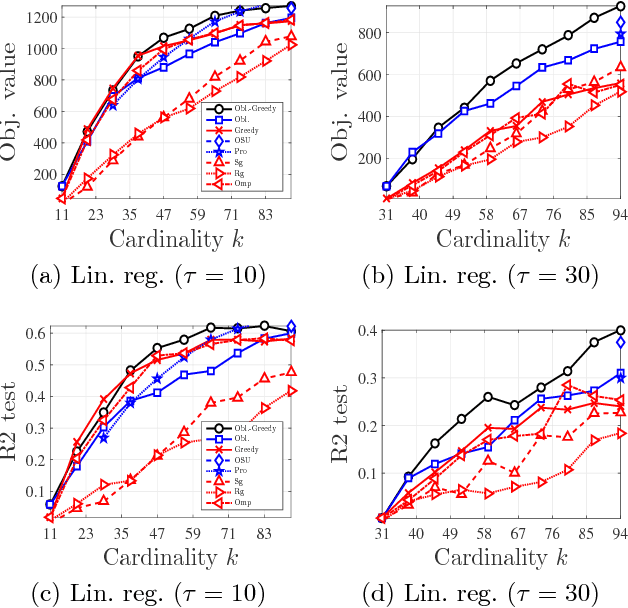
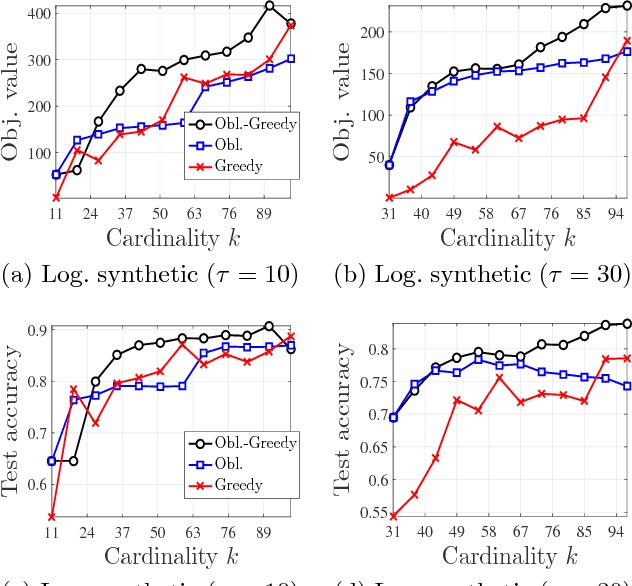
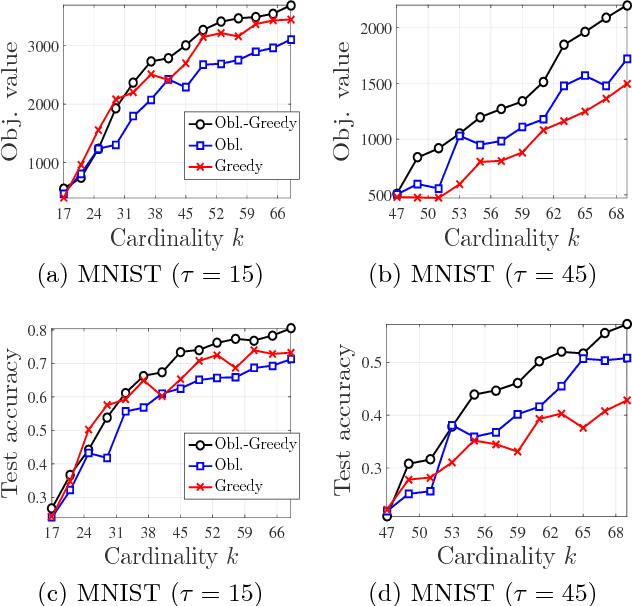
We study the problem of maximizing a monotone set function subject to a cardinality constraint $k$ in the setting where some number of elements $\tau$ is deleted from the returned set. The focus of this work is on the worst-case adversarial setting. While there exist constant-factor guarantees when the function is submodular, there are no guarantees for non-submodular objectives. In this work, we present a new algorithm Oblivious-Greedy and prove the first constant-factor approximation guarantees for a wider class of non-submodular objectives. The obtained theoretical bounds are the first constant-factor bounds that also hold in the linear regime, i.e. when the number of deletions $\tau$ is linear in $k$. Our bounds depend on established parameters such as the submodularity ratio and some novel ones such as the inverse curvature. We bound these parameters for two important objectives including support selection and variance reduction. Finally, we numerically demonstrate the robust performance of Oblivious-Greedy for these two objectives on various datasets.